5.Уравнения гидростатики для сжимаемых сред

Рассмотрим равновесие сжимаемой жидкости (газа), находящейся под действием только сил тяжести. В качестве примера рассмотрим изменение давления воздуха по высоте атмосферы. Направим координатную ось вертикально вверх. Тогда основное дифференциальное уравнение статики (2.4) будет иметь вид

dp = gdz. (2.14)

Т.к. воздух  сжимаемая среда, необходимо учитывать зависимость плотности от температуры и давления, что можно сделать, используя уравнение Клапейрона  Менделеева:

;

тогда учитывая зависимость температуры от высоты, из (2.14) получим:

.

После интегрирования с учетом того, что на уровне z=z₀ давление р=p₀, получим

. (2.15)

Эта формула носит название барометрической. Если считать, что атмосфера находится в изотермическом равновесии, т.е. T(z)=const то

. (2.16)

Если задано линейное изменение температуры по высоте атмосферы T=T₀b(zz_o), что справедливо до z=11 км, барометрическая формула примет вид:

. (2.17)

Другой вариант барометрической формулы можно получить, приняв температуру одинаковой по высоте и используя закон Бойля  Мариотта. Подставляя в уравнение (2.14)

 = ₀ ,

разделяя переменные и интегрируя, получим

. (2.18)

Вводя обозначение и решая относительно р, получим еще один вариант барометрической формулы:

. (2.19)

Если записать (2.17) для двух высот z₁ и z₂:

получим барометрическую формулу в виде:

, (2.20)

которая используется для определения высоты по измеренным значениям барометрического давления р₁ и р₂.

Рисунок 2.6. Изменение давления, температуры и плотности по высоте атмосферы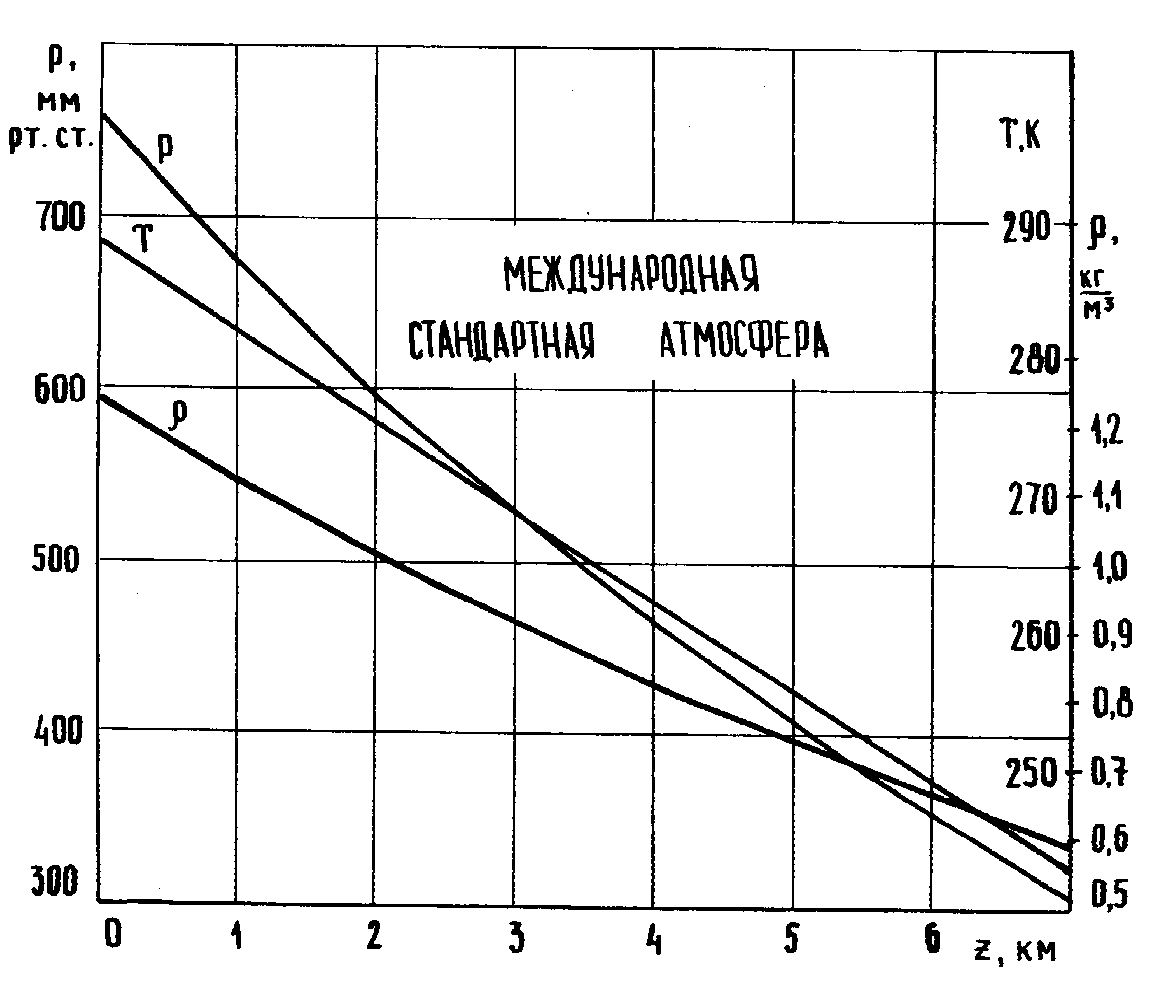

На рисунке 2.6 приведены параметры международной стандартной атмосферы (МСА). На поверхности Земли z₀ приняты нормальные атмосферные условия: Т=288, р= 760 мм.рт.ст. (101300 Па). В пределах 11 километров падение температуры принимается линейным (6,5°С на 1 км).

Объекты промтеплоэнергетики имеют относительно небольшую высоту (дымовые трубы  до 300400 м), поэтому на практике для определения изменения давления газа по высоте используют основной закон гидростатики для несжимаемой жидкости:

p = p₀(zz₀)g.

Если высота объекта не более 400 м, погрешность этой формулы не превышает 0,5 %, что вполне допустимо для технических расчетов.

6.Статика двух газов. Дымовая труба

В некоторых промтеплоэнергетических установках, например, паровых котлах или промышленных печах, имеет место взаимное действие горячих газов (продуктов сгорания топлива), заполняющих установку, и относительно холодного атмосферного воздуха, окружающего установку. Плотность продуктов сгорания, состоящих в основном из углекислого газа СО₂, водяных паров Н₂0, азота N₂ и кислорода О₂, при н.ф.у, близка к плотности воздуха (_г0 = 1,25  1,35 кг/м³; _в0 = l,29 кг/м³), но при высокой температуре становится значительно ниже:

t, °C	0	200	500	1000	1500	2000
, кг/м3	1,30	0,664	0,459	0,279	0,201	0,156

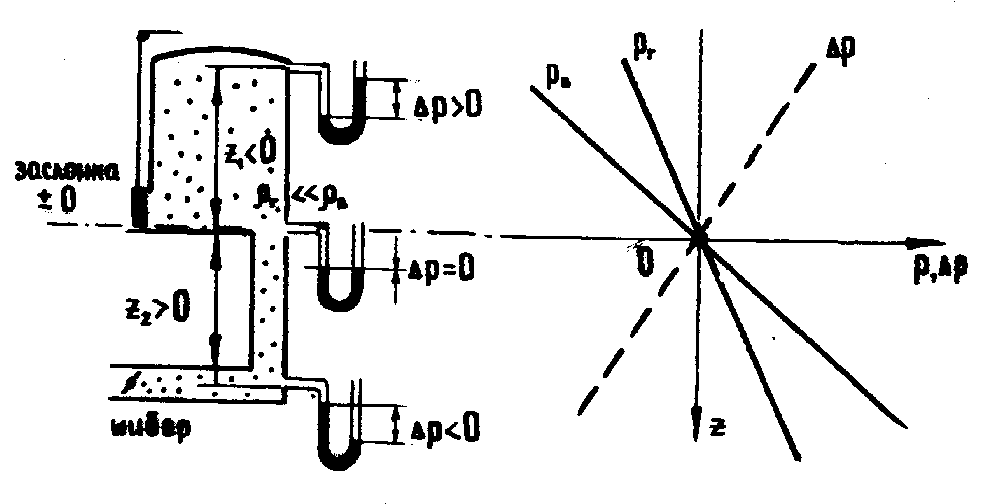Поэтому здесь мы говорим о взаимодействии газа легкого и тяжелого газов, разделенных некоторой преградой; что является следствием такого взаимодействия, рассмотрим на следующем примере. На рис. 9 схематично показана рабочая камера печи с участком дымохода, заполненного горячими продуктами сгорания, плотность которых намного меньше плотности окружающей атмосферы (_г<<_в). Если топливная горелка отключена, шибер закрыт, а заслонка рабочего окна немного приподнята, то будет наблюдаться равновесие печных газов и окружающей атмосферы, вследствие чего не будет ни выбивания газов, ни засасывания воздуха в печь через приоткрытое окно. Таким образом, на уровне печного окна абсолютное давление печных газов равно давлению окружающего воздуха, т.е. избыточное давление газов равно нулю. Этот уровень обычно называют нулевой линией 0. Направим координатную ось Oz вертикально вниз от нулевой линии, а ось абсолютных и избыточных давлений направим горизонтально

Рисунок 2.7 Статика двух газов

вправо (рисунок 2.7).

Линии абсолютного атмосферного давления

p_в = p₀+zg_в

и абсолютного давления печных газов

p_г= p₀+zg_г

проведем через начало координат. (Здесь p₀  абсолютное давление на уровне z= 0). Отметим, что вторая линия пройдет более круто чем первая, т.к. печные газы имеют плотность меньше чем атмосфера. Избыточное давление газов

p = p_гp_в

будет положительным выше нулевой линии и отрицательным  ниже. Проведем мысленный эксперимент по измерению избыточного давления газов с помощью дифференциального Uобразного манометра под сводом печи на уровне z₁<0, на нулевой линии (z₀=0) и в дымоходе на уровне z₂> 0.

Избыточное давление на уровне z₁:

p = p_г1p_в1 = (p₀z₁_гg)(p₀z1_вg)=z₁_гg+z₁_вg=z₁g(_г_в).

Т.к. _в>_г то р>0. Избыточное давление на уровне z₂:

p = p_г2p_в2=(p₀+z₂_гg)(p₀+z₂_вg)=z₂_гgz₂_вg=z₂g(_г_в).

Т.к. _в>_г то р<0). Таким образом, манометры покажут положительное избыточное давление печных газов под сводом печи и отрицательное избыточное давление (разряжение)  в дымоходе. На нулевой линии уровень жидкости в левой и правой ветвях манометра будут одинаковыми. Если топливная горелка включена, шибер открыт, и продукты горения удаляются через дымоход в дымовую трубу, то положение нулевой линии в печи можно отрегулировать дымовым шибером: закрывая шибер будем опускать нулевую линию, а следовательно повышать избыточное давление на уровне печного окна и вероятность выбивания печных газов а атмосферу; открывая шибер будем поднимать нулевую линию.

Пример Рассчитаем значение избыточного давления под сводом мартеновской печи: z= 4 м, _г=0,17 кг/м³ при t_г=1900 °С, _в== 1,20 при t= 20 °С, давление на уровне порога завалочных окон p₀= 1 мм. вод. ст. Решение:

p_z=p₀+zg(_в_г)=19,8+49,8(1,200,17)=50,8 Па.

Статика дымовой трубы. Дымовая труба  это вертикальный канал большой высоты, через который отводятся горячие продукты сгорания с плотностью значительно меньшей, чем плотность окружающего атмосферного воздуха. Дымовая труба  это тяговое средство, предназначенное для создания разряжения (тяги), под действием которого продукты сгорания отсасываются из камеры промтеплоэнергетической установки, преодолевая сопротивление системы дымоходов. Механизм создания разрежения можно уяснить, рассмотрев статику дымовой трубы (рисунок 2.8). Предположим, что дымовой шибер опущен и движение газов в трубе прекратилось. В плоскости устья трубы давления газов и атмосферы равны между собой и составляют величину, количественно равную давлению всей атмосферы, лежащей выше дымовой трубы. По мере перемещения вниз от устья давление газов и атмосферы будет увеличиваться и у основания трубы составит

для газов: p_г1=p₀+Hg_г,

для атмосферы: p_в1=p₀+Hg_в.

Избыточное давление газов у основания трубы

p₁=p_г1p_в1=Hg(_г_в),

Рисунок 2.8 Статика домовой трубы

а т.к. _г<_в то p₁<0, т.е. у основания трубы будет наблюдаться отрицательное избыточное давление, или разрежение, что можно определить и экспериментально, применив дифференциальный U  образный манометр (рис.10). Разрежение, или энергия отсоса, которое создает дымовая труба высотой Н, расходуется на преодоление сопротивления дымового тракта, или системы дымоходов, соединяющих рабочую камеру установки с трубой, следовательно

, (2.20)

где  суммарное гидравлическое сопротивление дымового тракта (см. раздел 5). Ориентировочную высоту дымовой трубы (без учета сопротивления трубы) определяют из выражения:

(2.21)

Расчет высоты дымовой трубы производят для летних, наиболее тяжелых условий, когда плотность воздуха минимальна. Рассмотрим два примера.

Пример 1: требуется рассчитать тягу дымовой трубы высотой Н=100м в зимнее (t_в = 20 °C), осеннее (t_в = 0 °С) и летнее (t_в = 30 °С) время; температура продуктов сгорания t_г = 300°С, плотность _г0 = l,32 кг/м³.

Решение: рассчитаем плотность продуктов сгорания и воздуха при действительных условиях:

,

,

,

.

Тяга дымовой трубы:

зимой p=1009,8(1,390,63)=745 Па,

осенью p=1009,8(1,290,63)=647 Па,

летом p=1009,8(1,16  0,63)=520 Па.

Как видно из этого примера, тяга дымовой трубы летом примерно в 1,5 раза хуже, чем зимой.

Пример 2: требуется определить ориентировочно высоту дымовой трубы для условий: суммарное сопротивление дымового тракта р=400Па; плотность дымовых газов _г0=1,3 кг/м³; температура газов 285°С.

Решение: принимаем температуру наружного воздуха в летнее время 35°С; тогда плотности газов и воздуха равны:

,

,

и высота дымовой трубы

.