40.Потери давления при движении пароводяных смесей.

Потери на трение при движении пароводяной смеси при постоянном паросодержании (необогреваемая труба рис. 10.1.б) определяется по формуле:

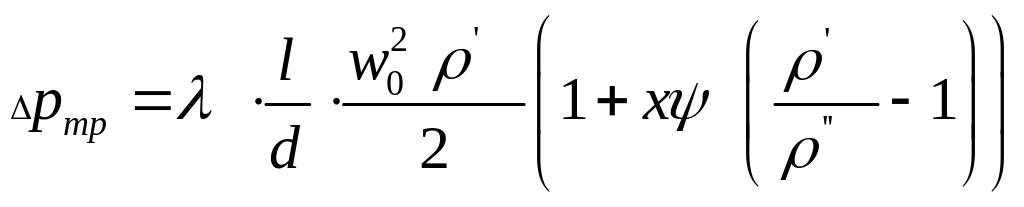Па, (10.4)

где   коэффициент скорости,  = f(x,p,w₀), находятся по номограммам в специальной литературе.

Потери на трение при переменном паросодержании (рис. 10.1.а, обогреваемая труба) :

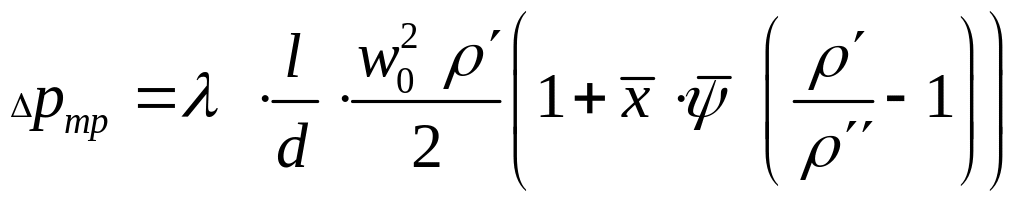Па, (10.5)

где  среднее паросодержание на участке длиной “l”

 средний коэффициент скорости

. (10.6)

Потери давления в местных сопротивлениях рассчитываются по формуле:

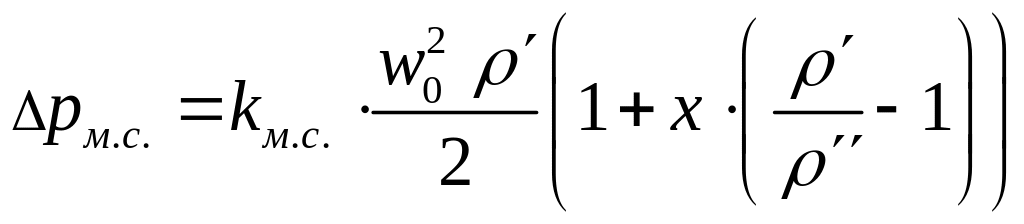, (10.7)

где k_м.с.  коэффициент местного сопротивления.

Потери геометрического давления (нивелирный перепад давлений) определяется по формуле

, (10.8)

где  средняя действительная плотность пароводяной смеси, кг/м³,

, (10.9)

где  среднее напорное паросодержание, определяемое по номограммам в специальной литературе.

Суммарные потери давления на трение и местные сопротивления сложной системы, состоящей из совокупности последовательно присоединенных сопротивлений одного трубного элемента рассчитываются по формуле:

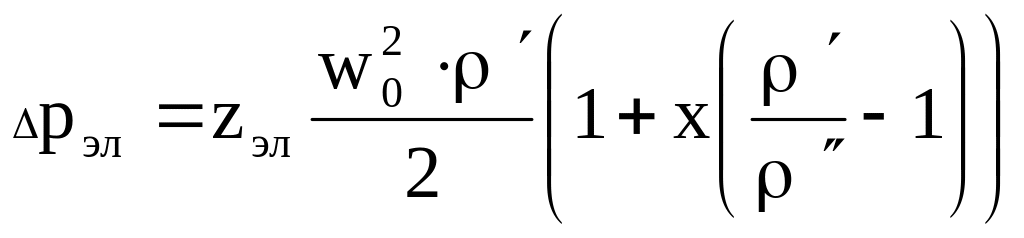(10.10)

где z_эл  полный коэффициент сопротивления,

(10.11)

Рисунок 10.2. Элемент, состоящий из системы параллельных труб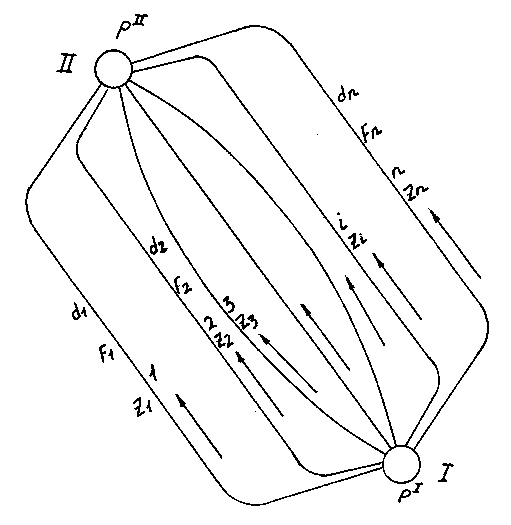

В элементе, состоящем из системы параллельных труб разного диаметра, длины и конфигурации, может быть известен общий расход пароводяной смеси, но не известны расходы по отдельным трубам. Очевидно, что сопротивление каждой трубы, соединяющей коллекторы I и II (рис. 10.2) одинаковы и равны разности давлений в колекторах (p^I и p^II). Полный коэффициент сопротивления элемента, состоящего из нескольких параллельных труб, определяется по формуле

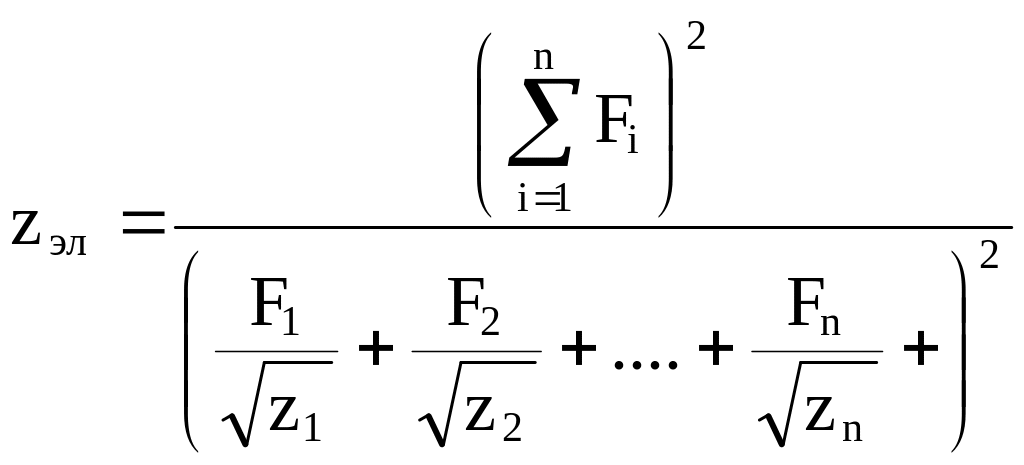, (10.12)

где z₁, z₂, … ,z _n  полные коэффициенты сопротивления отдельных труб, определяемые по (10.11);

F₁,F₂, … ,F_n  сечения этих труб, м²;

Условная скорость w₀  в (10.10) определяется по формуле

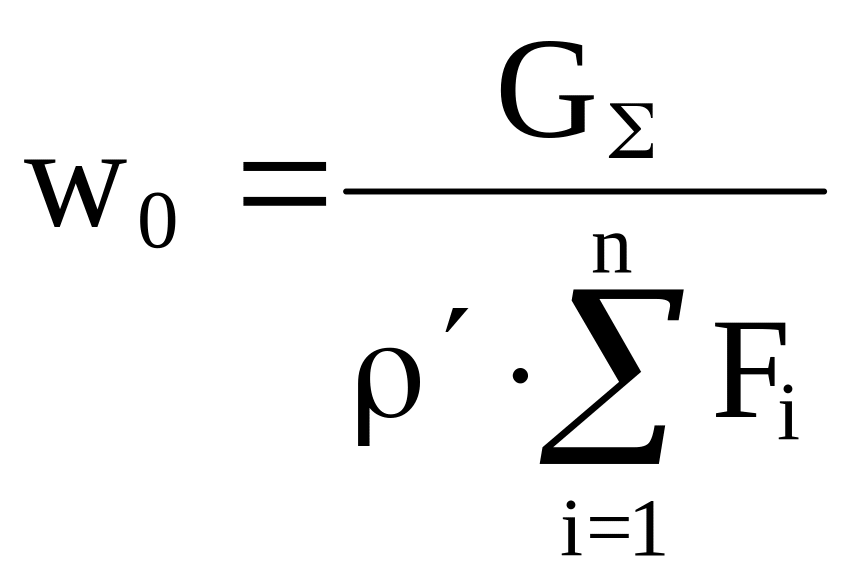, (10.13)

где G_  суммарный массовый расход пароводяной смеси, проходящей по всем параллельным трубам, кг/с;

 суммарное сечение всех параллельных труб, м².

41.Контур естественной циркуляции

В паровых котлах с естественной циркуляцией движение воды и пароводяной смеси в испарительной системе осуществляется за счет давления, создаваемого разностью плотности воды в опускных трубах и пароводяной смеси в обогреваемых подъемных трубах системы. Простейший контур естественной циркуляции (рис. 10.3) состоит из барабанасепаратора 1, в котором происходит разделение пароводяной смеси на пар и воду, необогреваемой опускной трубы 2, соединительного коллектора 3 и обогреваемой подъемной трубы 4. За счет подвода теплоты в какой-то точке по высоте подъемной трубы происходит закипание воды, и выше этой точки находится пароводяная смесь. Участок ниже точки называется экономайзерным (h_эк), выше  паросодержащим (h_пар). Естественно, что средняя плотность воды и пароводяной смеси в подъемных трубах _см меньше, чем плотность воды в опускных трубах . Величина

p = hg(  _см),Па (10.14)

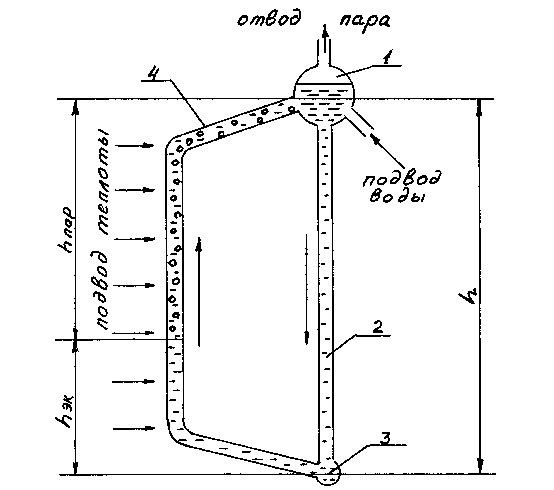
Рисунок 10.3. Контур с естественной циркуляцией

называется движущим дав­лением циркуляции. Назначение движущего давления  преодолеть гидравлическое сопротивление элемента

p = p_эл, (10.15)

где p_эл  гидравлическое сопротивление контура, состоящего из сопротивления подъемной и опускной труб

p_эл = p_оп+р_под. (10.16)

Разность движущего давления и сопротивления подъемной части контура циркуляции составляет полезное давление

р_пол = р  р_под, (10.17)

расходуемое на преодоление опускной части контура

р_пол = р_оп. (10.18)

Рисунок 10.4. Гидравлическая характеристика простого циркуляционного контура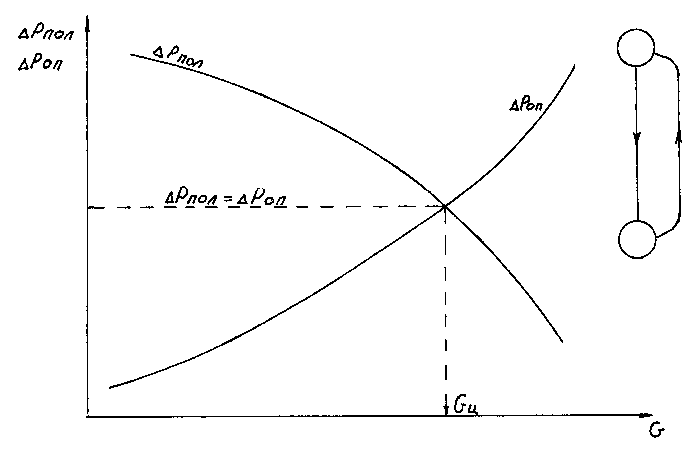

Т.к. движущее давление р, рассчитываемое по формуле (10.14), практически не зависит от расхода воды и пароводяной смеси в контуре циркуляции G, а гидравлическое сопротивление подъемной р_под и опускной р_оп труб, включающие потери на трение и в местных сопротивлениях, пропорциональны квадрату расхода (скорости, фла (10.10)), то при увеличении расхода G полезное давление p_пол (10.17) падает, а сопротивление опускной трубы  возрастает. Принцип расчета простого циркуляционного контура заключается в том, чтобы найти такой расход G_ц, при котором выполняется условие (10.18). Задаваясь разными значениями расхода, рассчитываем зависимости p_пол=f(G) и p_оп=f(G). Пересечение этих кривых на графике (рис. 10.4) дает возможность определить искомый расход воды и паровой смеси простого циркуляционного контура G.

Рисунок 10.5. Гидравлическая характеристика сложного циркуляционного контура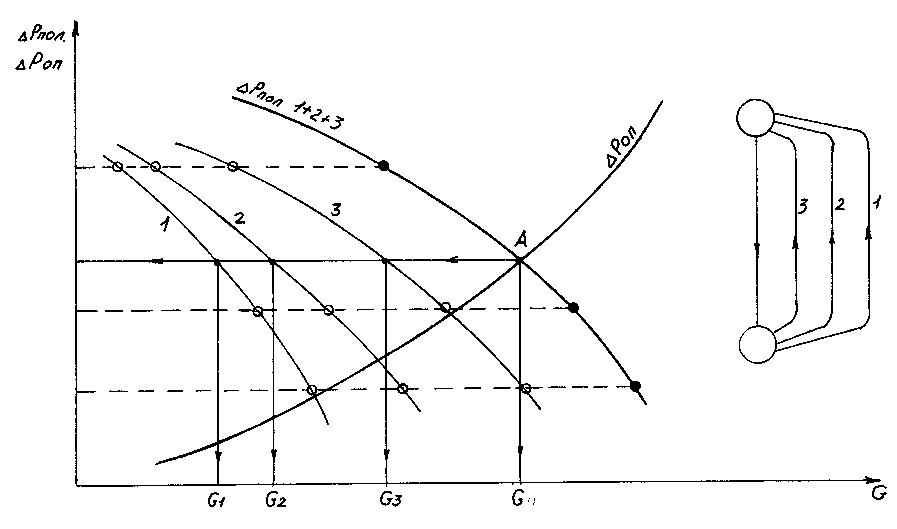

Испарительный пучок, состоящий из нескольких рядов подъемных труб разной длины, и одну общую опускную трубу, называют сложным циркуляционным контуром. Определение расхода воды в контуре производится следующим образом. Пусть сложный контур состоит из трех рядов труб (рис. 10.5). Задавая различные значения расхода G, рассчитывают и строят зависимости р_пол = f(G) для трех рядов (кривые 1,2,3). Складывая G для одинаковых значений p_пол отдельных рядов, строят суммарную зависимость p_пол1+2+3=f(G). Затем рассчитывают и строят зависимость сопротивления опускной трубы от расхода p_оп=f(G). Расчетная точка А находится на пересечении кривых и дает возможность определить сумарный расход в сложном контуре G_ц и расходы в каждом ряде труб G₁, G₂ и G₃, причем G_ц= G₁+ G₂+ G₃. Если паропроизводительность котла равна D, то отношение G_ц : D называется кратностью циркуляции:

, (кг/кг).

С увеличением тепловой нагрузки (интенсивности подвода теплоты) паропроизводительность увеличивается, а кратность циркуляции уменьшается. При уменьшении тепловой нагрузки кратность циркуляции возрастает, т.к. движущее давление уменьшается в меньшей степени, чем сопротивление опускных труб. Так, при уменьшении производительности вдвое кратность циркуляции возрастает в 1,6 раз.