36. Метод гидравлического моделирования

Метод гидравлического моделирования  это метод изучения гидрогазодинамических процессов тех или иных объектов промтеплоэнергетики на моделях. Теория подобия определяет следующие требования к модели:

 модель и образец должны быть геометрически подобны по внутренним контурам;

 необходимо, чтобы величины, входящие в краевые условия образца и модели были пропорциональны. Таким образом обеспечивается подобие на входе в модель;

 физические величины должны изменятся в объеме модели по тому же закону, что и в образце;

 определяющие критерии в модели и образце должны быть равны.

На практике выдержать все эти требования невозможно, т.к. исследований на гидравлических моделях производятся в изотермических условиях (моделирующие агенты  воздух или вода  имеют, как правило, комнатную температуру), а в образце обычно наблюдается весьма неравномерное температурное поле, т.е. образец неизотермичен. Поэтому всякое гидравлическое моделирование, как и любое другое моделирование, является приближенным. В то же время погрешности приближенности гидравлического моделирования сводятся к минимуму, благодаря особым свойствам вязкой жидкости: стабильности и автомодельности.

Стабильностью называется свойство вязкой жидкости принимать характерное для данного режима течения (ламинарного и турбулентного) распределения скоростей, как бы не изменялась картина этого распределения при действии внешних сил.

Автомодельностью называется свойство вязкой жидкости устанавливать в пределах каждого режима (ламинарного и турбулентного) подобное распределение скоростей по сечению потока независимо от абсолютного значения скорости. Суть этого свойства в том, что если модуль и образец находятся в режиме автомодельности, то они способны моделировать самое себя. Это значит, что при снижении (повышении) расхода моделирующего агента, безразмерные эпюры скоростей не изменяются.

Рисунок 9.3. Автомодельные области при течении вязкой жидкости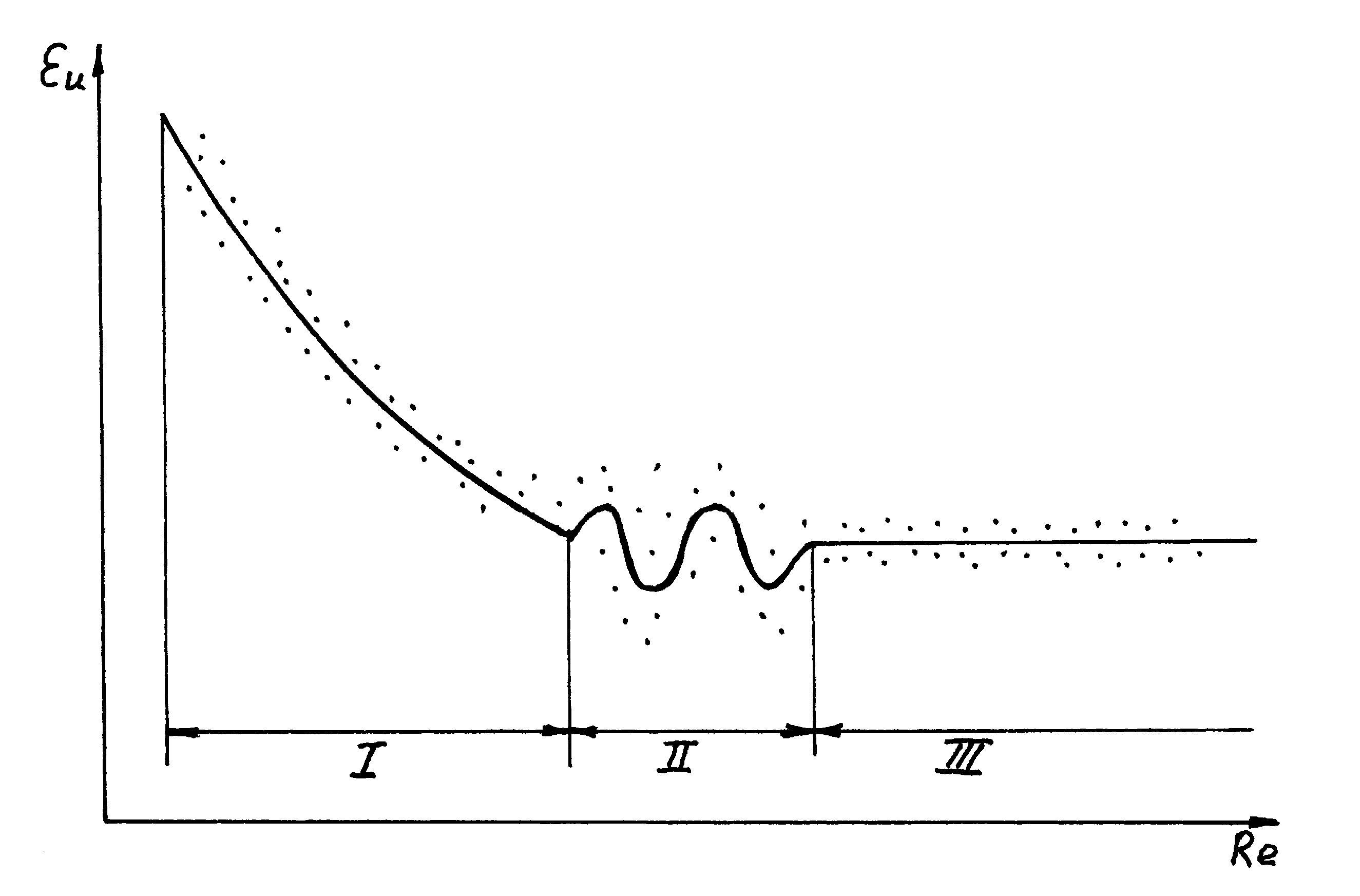

Наличие автомодельности проверяются экспериментально путем исследования зависимости числа Эйлера от числа Рейнольдса :

Eu =  (Re) ,

которая имеет вид показанный на рисунке 60. Эта зависимость получается следующим образом. На модели измеряют перепад давлений между какими-либо двумя точками р и расход моделирующего агента; по расходу определяют скорость w в характерном сечении. Затем рассчитывают значение числа Эйлера по формуле Еu=p/(w²) и число Рейнольдса по формуле Re = (wd)/. Изменяя расход в достаточно большом диапазоне, получают зависимость (рис 9.3). В полученной зависимости Еu =  (Re) можно выделить следующие участки :

I  первая автомодельная область, соответствующая ламинарному течению, для которой характерно постоянство произведения чисел Эйлера и Рейнольдса :

Eu Re = const; (9.19)

II  переходной участок, на котором автомодельность отсутствует;

III  вторая автомодельная область, соответствующая турбулентному течению, для которой характерно постоянство числа Рейнольдса:

Re   (Eu) = const (9.20)

Из практики моделирования известно, что вторая автомодельная область существует всегда, если Re > 10000, т.е. при развитом турбулентном течении. Практически в гидравлическом моделировании используют именно эту область.