35.1. Метод анализа размерностей

Рисунок 9.2 - К исследованию силы лобового сопротивления аппарата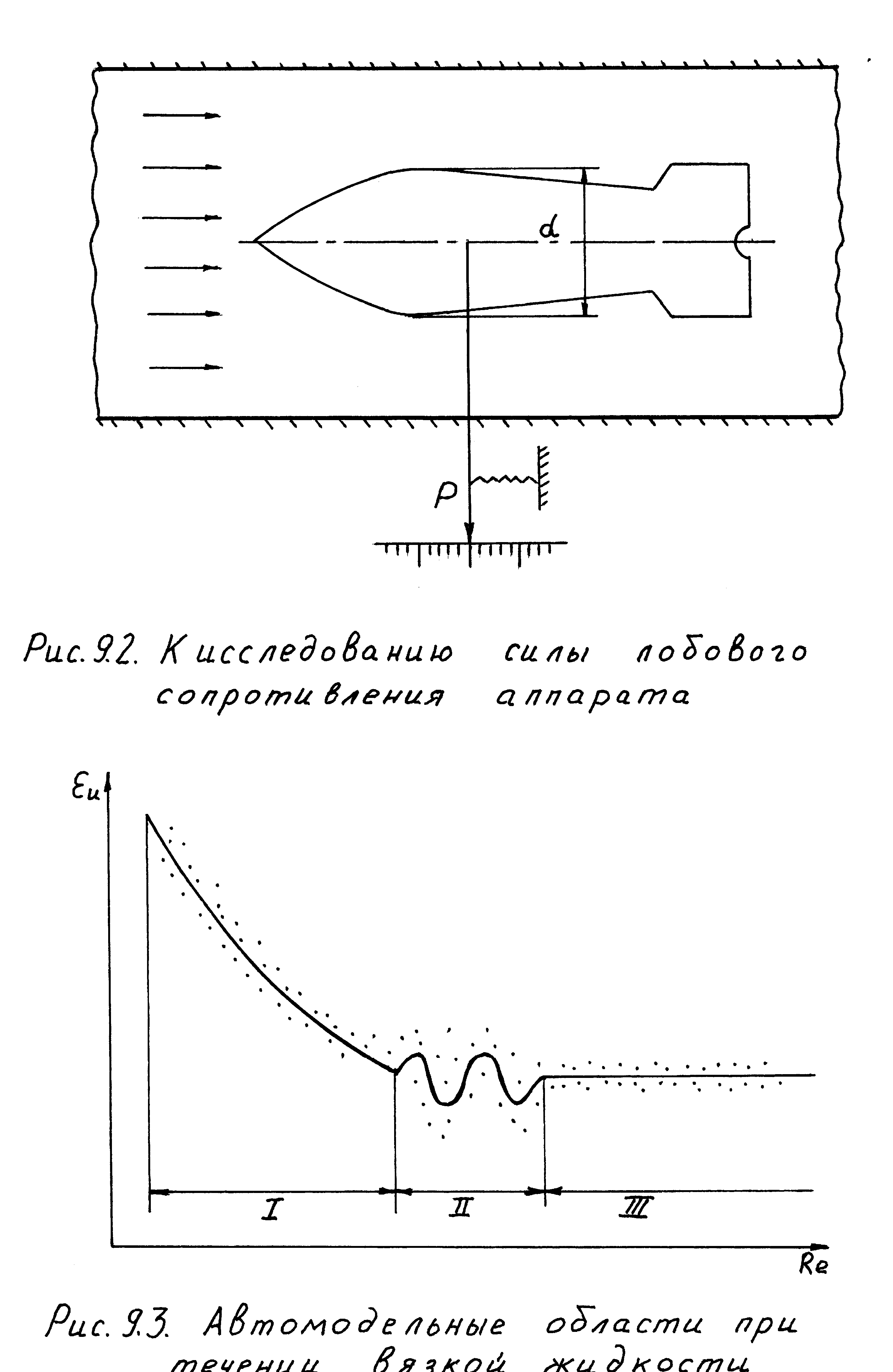

Метод анализа размерностей рассмотрим на примере исследования силы лобового сопротивления аппарата. Процесс получения критериев подобия может быть разделен на следующие этапы.

1) Постановка задачи. Некоторый гидро (аэро)динамический аппарат с характерным линейным размером d находится в потоке жидкости, движущейся со скоростью w (рис.9.2). Необходимо исследовать силу лобового сопротивления аппарата. Выявляем величины, которые могут повлиять на силу P. Такими величинами, по нашему мнению, помимо скорости и линейного размера, могут быть теплофизические свойства жидкости  плотность  и динамическая вязкость  . Поэтому силу лобового сопротивления будем считать следующей функцией:

P =  (w, d, , ), (9.10)

т.е. в общем случае это функция 4х переменных.

2) Запись функции (9.10) со степенями при независимых переменных :

P =  (w ^a,d ^b,^c ,  ^e ) (9.11)

3) Составление таблицы размерностей. Введем обозначение независимых единиц измерения:

длины, м  L,

массы, кг  M,

времени, с  T.

Тогда единицы измерения величин в функции (9.10) могут быть представлены следующим образом:

единица силы P  H =  MLT^2

скорости w  м/с  LT^1

длины d  м  L

плотности   кг/м³  ML^3

коэффициента динамической

вязкости    ML^1T^1

4) Запись функции (9.11) в размерностях:

(9.12)

5) Составление системы уравнений для удовлетворения требования однородности размерности (размерности левой и правой частей функции должны быть равны):

для M: 1= с + е (9.13)

L: 1= a + b  3 c  e (9.14)

T: 2 =  a  e (9.15)

6) Решения системы уравнений (9.139.15). В системе трех уравнений имеется 4 неизвестных. Решить такую систему можно, если принять одно из них, например е, за известное (вообще может и большее количество лишних неизвестных, тогда за известные принимаются два, три и т.д. неизвестных). Решая систему, получаем:

из (9.13) с=1е ,

из (9.15) а=2е ,

из (9.14) b=2е .

7) Записать уравнения (9.11) с найденными значениями системы:

P = f (w^2e , d^2e , ^{1  e} , ^e) (9.16)

8) Объединение величин в комплексы. Сначала объединяем величины без буквенных степеней, перемножая их, при этом при перенесении таковых из правой части уравнения в левую изменяем знак степени:

.

Назовем полученный комплекс “коэффициент лобового сопротивления” и обозначим К_л.с. Заметим, что полученное выражение является аналогом критерия Эйлера. Затем объединим величины, имеющие буквенную степень “е” и перемножим их:

.

Полученный комплекс является обратным выражением критерия Рейнольдса.

9) Запись безразмерного (критериального) уравнения

К_л.с. =  (Re). (9.17)

Как видим, вместо пяти размерных величин в исходном размерном уравнении в безразмерном уравнении имеется всего два что соответствует теореме Бекингема.

10) Проведение экспериментальных исследований, обработка результатов и получение эмпирических уравнений производится так же, как и 4й этап метода масштабных преобразований.

Следует отметить, что метод анализа размерности оригинален, прост, но требует от исследователя достаточных знаний, опыта и интуиции при выборе величин, характерных для изучаемого явления.