30.Струя, втекающая в полость. Струйный аппарат

Если свободную струю ограничить со всех сторон на некотором расстоянии от сопла (рисунок 56), то поверхность струи, увлекающая окружающую среду, сокращается, нерастраченная энергия расходуется на совершение работы противодавления, а у основания струи создается давление меньшее, чем в последующих сечениях. В результате создаются зоны пониженного давление в камерах теплоэнергетических установок, что в некоторых случаях может привести к вредным присосам холодного атмосферного воздуха. В других случаях эффект эжекции используется в специальных устройствах, называемых струйными аппаратами. Простейший струйный аппарат состоит из рабочего сопла 1 и смесителя 2 (рисунок 8.10). Рабочий поток, выходя из сопла с высокой скоростью, образует струю, которая после встречи со стенками смесителя перестает захватывать окружающую среду. Поэтому струя вовлекает в движение среду, находящуюся перед входом в смеситель. Поток, вовлекаемый в смеситель, называется инжектируемым. В отличие от свободной струи расход жидкости вдоль смесителя остается постоянным. Расчет струйных аппаратов производится или на основе уравнения импульсов, или на основе энергетического баланса. Последний для струй струйного аппарата записывается следующим образом (обозначения на рисунке 8.10):

Рисунок 8.10 - Струя, втекающая в полость. Схема струйного аппарата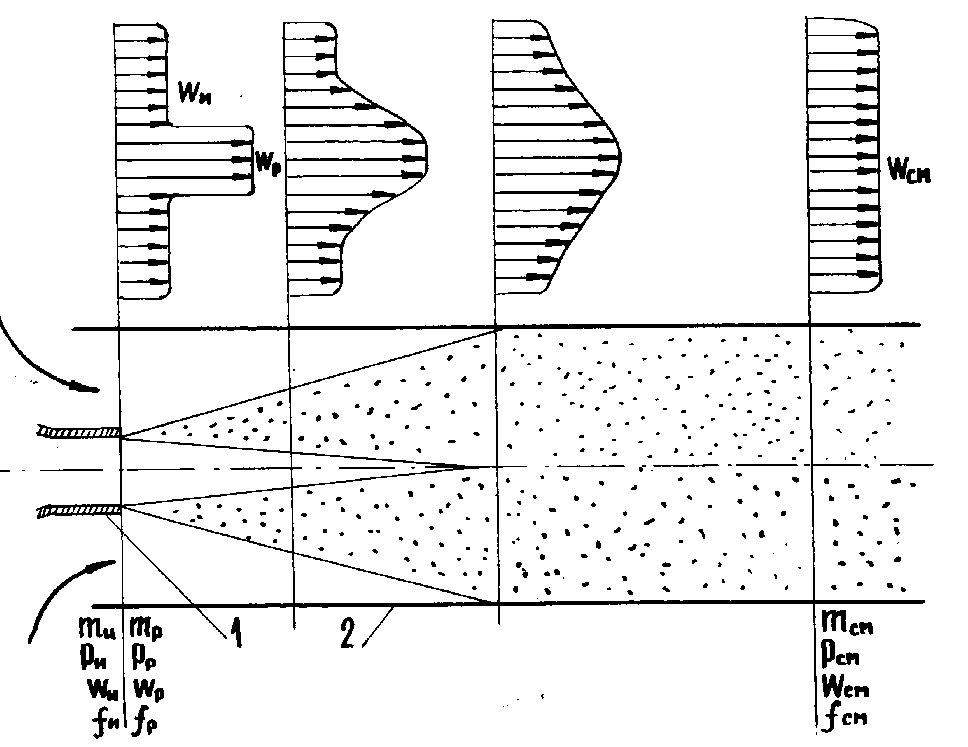

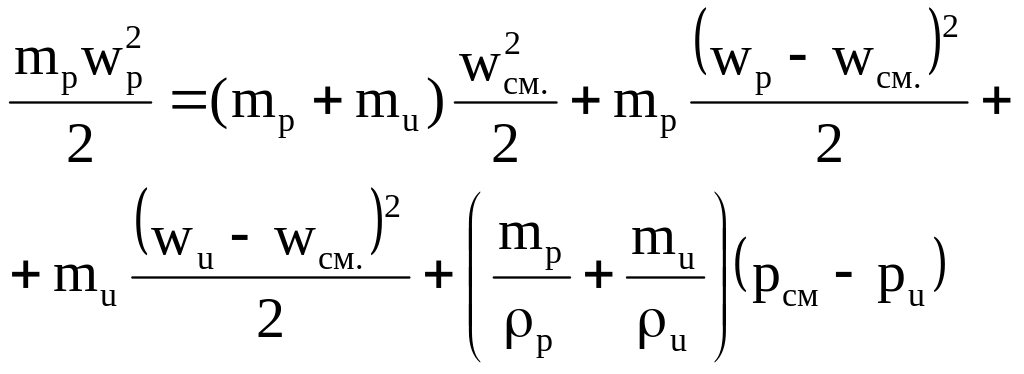(8.15)

В отличие от энергетического баланса свободной струи (уравнение 8.10), в правой части уравнения (8.15) имеется четвертое слагаемое, отображающее работу противодавления, которую совершает струя, перемещая объёмы рабочего и инжектируемого потоков из полости с меньшим (р_и) в полость с большим (р_см) давлением.

Струйные аппараты широко используются в промтеплоэнергетике в таких устройствах, как струйные насосы, эжекторы, инжекторы, инжекционные горелки и др. Важнейшей характеристикой всех этих устройств является массовая кратность инжекции, представляющая собой отношение массового расхода инжектируемой среды к массовому расходу рабочего потока:

31.Взаимодействие свободных струй

При соударении свободные струи расплющиваются, причем тем больше, чем больше угол встречи и количество движения струй. Направление результирующей струи (рисунок 8.11) определяют по диагонали параллелограмма, сторонами которого служат количества движения струй. Дальнобойность результирующей струи тем меньше, чем больше деформация при соударении.

Рисунок 8.11 - Взаимодействие свободных струй

а  струи встречаются под углом

б  оси струй параллельны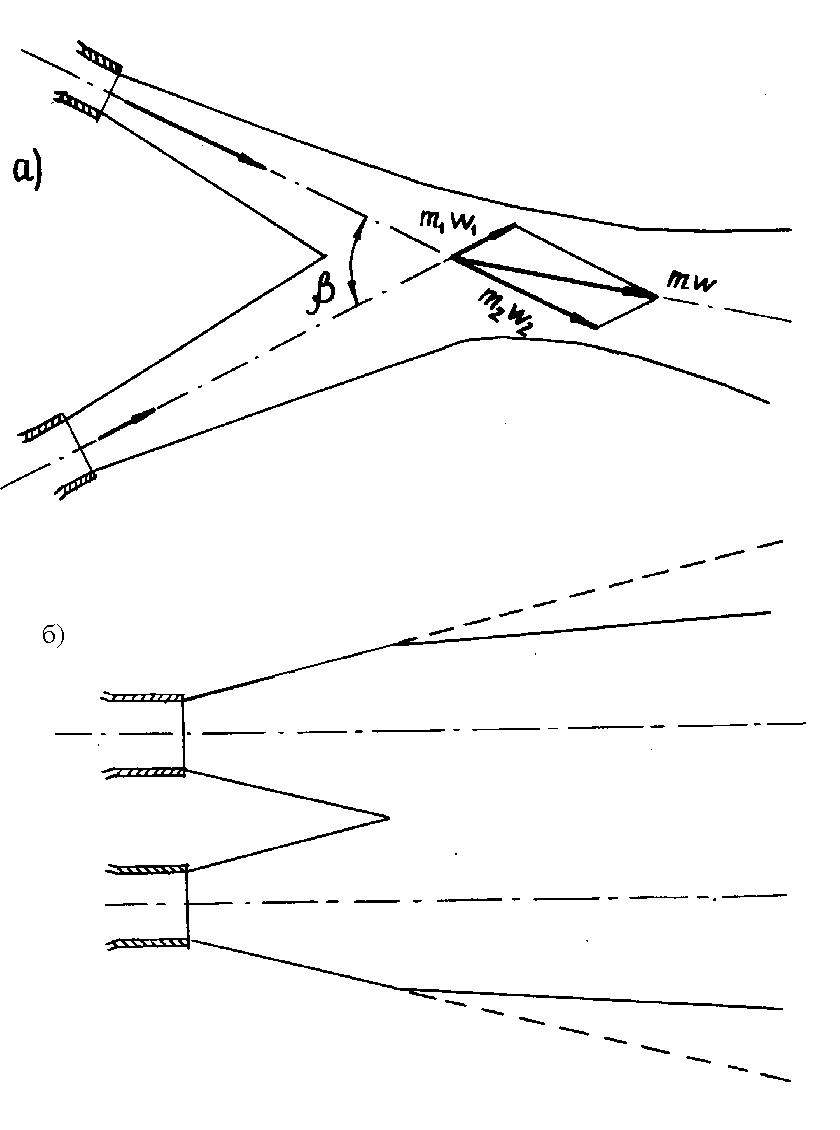

Если оси двух струй параллельны и находятся на достаточно близком расстоянии друг от друга (рисунок 8.11,б ), то взаимодействие между ними приводит к сокращению поверхности, через которую поступает окружающая среда. В результате угол раскрытия уменьшается, а дальнобойность увеличивается

9 Экспериментальные исследования гидродинамических процессов

32.Задачи исследований. Гидравлическое моделирование и теория подобия

В практике проектирования, эксплуатации и реконструкции промтеплоэнергетических установок (ПТУ) возникают проблемы с получением информации о распределении скоростей, ускорений и давлений в объеме или на поверхностях установок. В общем случае движение описано в дифференциальной форме (уравнения НавьеСтокса, энергии, неразрывности). Для интегрирования уравнений, т.е. получения аналитического решения, необходимо сформулировать условия однозначности, которые выделят конкретные явления из всего класса (форма, граничные и начальные условия, теплофизические свойства жидкости). Заметим, что рабочие камеры ПТУ, как правило, имеют весьма сложную форму, загромождены поверхностями нагрева или нагреваемыми (охлаждаемыми) телами, поэтому движение жидкости (газов) становится многомерным с наличием прямых и обратных потоков, зон рециркуляции и т.д.; в ряде случаев приходится иметь дело с неустановившимся неизотермичным нестационарным движением вязких сжимаемых жидкостей. В этих условиях интегрирование системы дифференциальных уравнений, в которую входят нелинейные уравнения высокого порядка в частных производных, практически невозможно  как из-за сложности происходящих процессов, так и из-за громоздкости математического описания. В таких случаях приходится прибегать к экспериментальным исследованиям, которые можно выполнять как на действующем объекте, так и на его модели. Работающие объекты почти всегда малодоступны для исследований, и удается получить только ограниченную информацию о движении потоков. Поэтому чаще эксперименты проводятся на модели, которая абсолютно доступна для исследований, а если объект находится на стадии проектирования, то модель является единственным средством получения нужной информации.

Исследования на модели проводятся на основе теории подобия и метода гидравлического моделирования. Теория подобия определяет условия физического подобия образца (моделируемого объекта) и модели, а также правила переноса результатов моделирования с модели на образец. Теорию подобия называют также методом обобщенных переменных потому, что она имеет дело не с размерными величинами, а безразмерными комплексами, которые называют критериями (или числами) подобия и которые являются обобщенными переменными. Количество критериев подобия, характерных для данного явления, меньше, чем количество размерных величин, и это значительно упрощает анализ исследуемых явлений. Например, целью исследования является определение зависимости гидравлического сопротивления объекта (p) от скорости (w), линейного размера (d), плотности () и вязкости () жидкости :

т.е. необходимо исследовать функцию четырех переменных. Использование теории подобия показывает, что исследуемые размерные величины объединены в двух обобщенных переменных, которыми являются :

число Эйлера

,

и число Рейнольдса

,

поэтому следует изучить очень простую зависимость  функцию одной переменной :

,

т.е. общее число переменных сократилось с пяти размерных до двух безразмерных.

Метод гидравлического моделирования, основанный на теории подобия, дает возможность подготовить и провести исследование на модели: выбрать геометрический масштаб модели, подобрать имитирующую жидкость (моделирующий агент) и расcчитать её расход, рассчитать режимы работы модели, получить формулы пересчета результатов моделирования на образец.