27.Струя во встречном и спутном потоках

На практике в промтеплоэнергетических установках свободная струя развивается не в спокойной среде, а во встречном, спутном или сносящем потоках. На рисунке 8.6 показаны эпюры скоростей в спутном и встречном потоках, которые получаются путем алгебраического суммирования скоростных профилей струи и среды.

В струе могут находиться какие-либо примеси, концентрация которых с_о отличается от концентрации в окружающей среде с_а; температура струи ,Т₀ также может отличаться от температуры окружающей среды Т_a. В общем случае w_aw₀, c_ac_o, T_aT₀. Выравнивание температур и концентраций физически происходит так же, как и выравнивание скоростей  в результате турбулентного перемешивания (роль молекулярной диффузии обычно мало). Таким образом, скоростные, концентрационные и температурные поля подобны, и поэтому справедливо соотношение

(8.11)

где с, Т и w - соответственно концентрация, температура и скорость в какой-либо точке струи

Рисунок 8.6 - Развитие струи в спутном (а) и встречном (б) потоке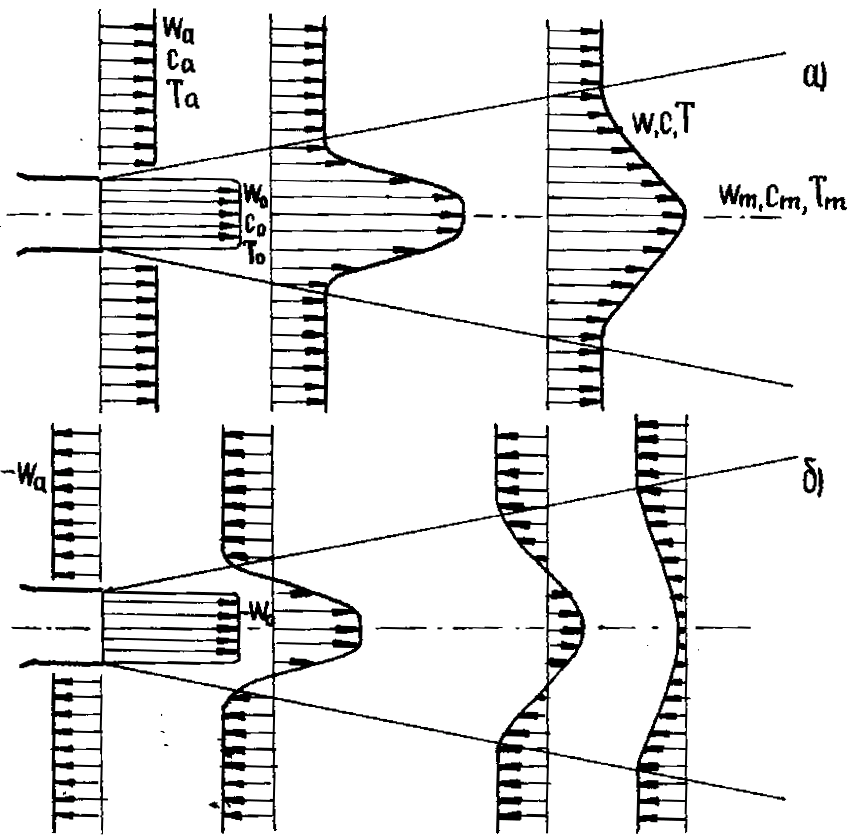

28. Струя, ограниченная параллельной плоскостью

Если направить струю параллельно твердой плоскости, расположенной на небольшом расстоянии от оси струи (рисунок 8.7), то дальнобойность струи увеличится; струя, развивавшаяся до встречи с плоскостью симметрично как свободная, после удара о поверхность деформируется и «стелится» по стенке. Это свойство В.Е. Грум  Гржимайло назвал настильностью. Настильность объясняется тем, что свободная поверхность струи, вовлекающая в движение новые массы, уменьшается, а затормаживающее действие присоединенной массы со стороны плоскости прекращается. Этим объясняется то, что по мере удаления от сопла максимум скоростей приближается к плоскости. В вертикальной плоскости и в горизонтальном осевом сечении струя развивается под меньшим углом, чем свободная (рисунок 8.7); угол растекания по плоскости равен 30°. Струя, развивающаяся параллельно плоскости, не оказывает на её давление.

29. Рисунок 8.7 - Схема струи, ограниченной параллельной плоскостью Струя, атакующая поверхность под углом

Если направить струю под углом  к плоскости (рисунок 8.8), то с увеличением угла атаки сплющивание увеличивается, а угол растекания можно определить по формуле В.И. Миткалинного:

_раст= 30+3 (8.12)

Струя оказывает давление на плоскость, максимум которого в месте встречи струи с плоскостью рассчитывается по формуле:

, (8.13)

где p_дин динамическое давление струи, Па,

,

где w_cp  среднее по сечению струи скорость в месте удара о плоскость, м/с.

р>0

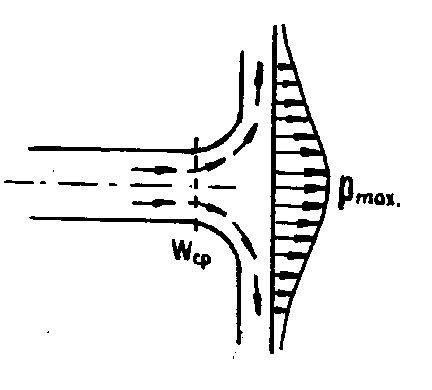
Рисунок 8.8 - Схема струи, атакующей поверхность под углом

Рисунок 8.9 - Струя, атакующая под прямым углом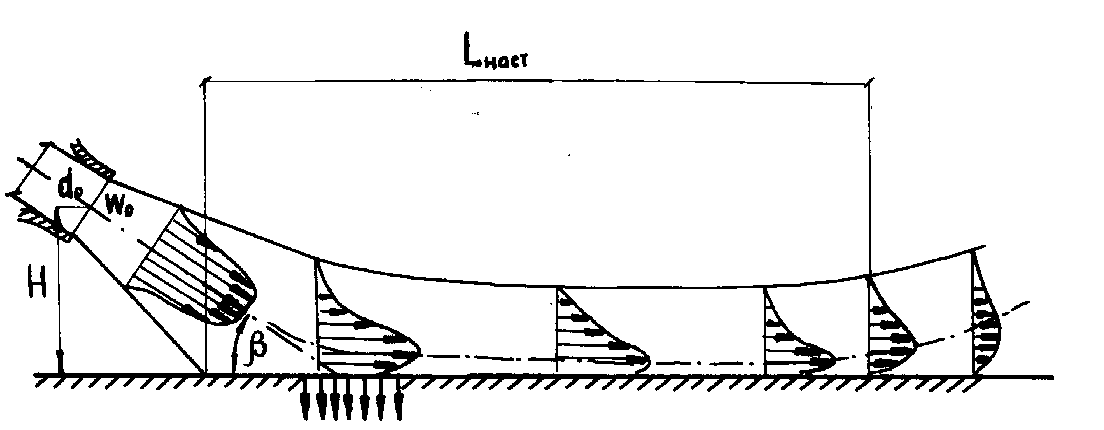

Дальнобойность атакующей струи уменьшается с увеличением угла атаки; настильность струи сохраняется на некотором расстоянии от места удара, а длина настильной части зависит от угла атаки , высоты сопла Н, начальной скорости w₀, плотности жидкости _ж и диаметра сопла:

. (8.14)

Струя, атакующая плоскость под прямым углом (рисунок 8.9) оказывает давление, максимум которого равен двум динамическим давлениям струи.