6. Истечение жидкостей и газов через отверстия, насадки и сопла

• Истечение капельных жидкостей, а также сжимаемых и несжимаемых газов происходит при работе таких устройств промтеплоэнергетики, как форсунки, газовые горелки, выхлопные трубы, газовые и паровые турбины, охлаждающие устройства и во многих других случаях. С истечением связаны и такие отрицательные явления, как выбивание дымовых газов из рабочих камер или присос атмосферного воздуха через отверстия и щели в стенках камеры и дымоходах.

• Истечение капельных жидкостей, а также «несжимаемых» газов (к последним относят газы, истекающие под действием малой разницы давлений, не превышающей 10% от абсолютного давления) представляет собой простой процесс перехода потенциальной энергии потока в кинетическую при практически неизменных плотности и температуре. При истечении «сжимаемых» газов происходит одновременно и реализация потенциальной энергии, и части внутренней энергии, т.е. идет термодинамический процесс расширения, сопровождающийся увеличением удельного объёма (или уменьшением плотности)

6.1 Истечение несжимаемых сред через отверстия

• 

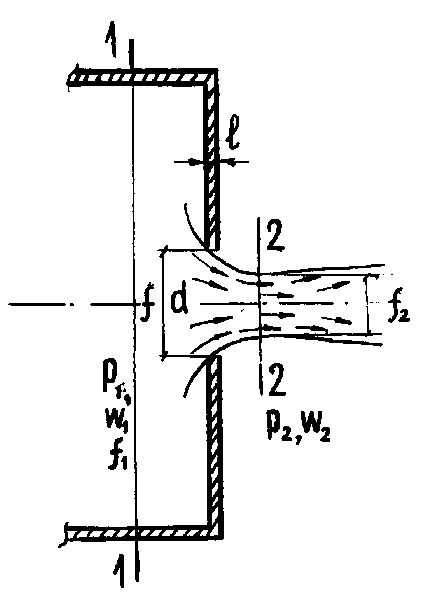
  Рисунок 6.1. Истечение из отверстия в тонкой стенке

  Рассмотрим истечение капельной жидкости или несжимаемого газа через отверстия в тонкой стенке ( l < d) большого резервуара (рисунок 6.1), в котором поддерживается постоянное давление р₁. Истечение происходит горизонтально в среду с давлением p₂<p₁. Форма истекающей среды такова, что самое узкое сечение струи f₂  больше сечения отверстия f и находится за отверстием. Запишем уравнение Бернулли для сечения 11, в котором поток в резервуаре ещё не деформирован, и в самом узком сечении струи 22: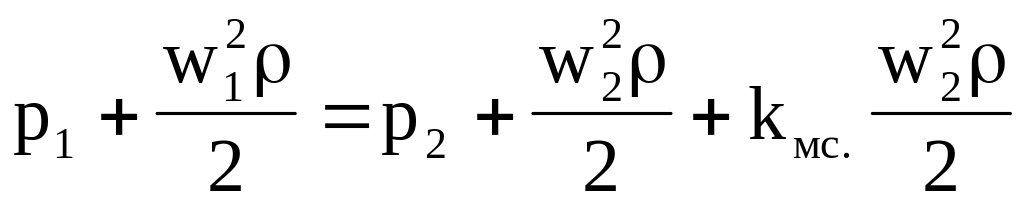

• ,

откуда

(6.1)

При истечении через отверстия k_м.с.=0,04...0,06, тогда коэффициент скорости

• ,

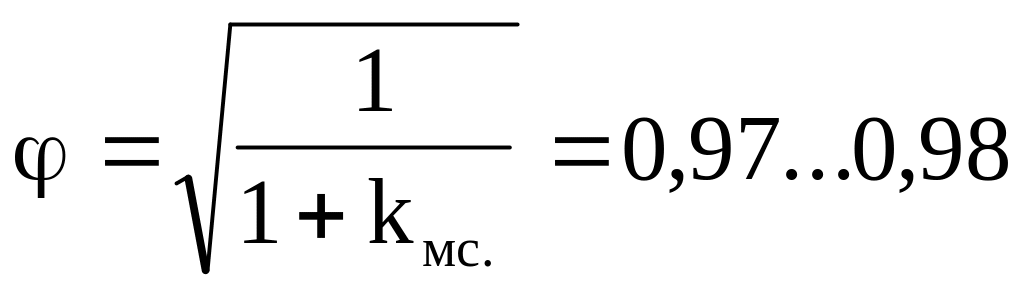Если f₂/f₁0, а =1, то получим известную формулу Торичелли :

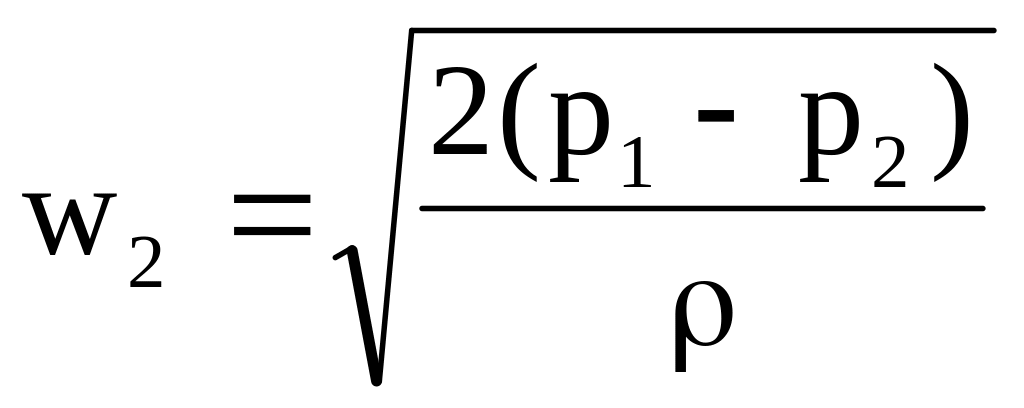• . (6.2)

Расход жидкости, истекающей через отверстия, равен

V=wf

Т.к. wf=w₂f₂ в соответствие с законом неразрывности, то

• 

где отношение f₂/f= называется коэффициентом сжатия, который принимается равным =0,63. Тогда расчетная формула для расхода примет вид:

(6.3)

Коэффициент расхода = учитывает сжатие струи и сопротивление отверстия и равен 0,61... 0,62.

6.2 Истечение несжимаемых сред через насадки

• • 

  Рисунок 6.2. Истечение через насадки

  Рассмотрим истечение жидкости через насадки, присоединенные к отверстию в стенке резервуара. Если насадок имеет цилиндрическую форму с острыми кромками на входе (рисунок 6.2а) и длину l 2,5d, то струя, истекающая из отверстия, успевает сначала сузиться, а затем расшириться до полного сечения насадка. В промежутке между сжатым сечением и стенками насадка образуется вихревая зона. Так как струя выходит из насадка полным сечением, то коэффициент сжатия (отношение сечений струй на выходе и входе насадка )  =1, а коэффициент расхода ==. Для определения коэффициента скорости  составим уравнение Бернулли для сечения 11 (здесь скорость жидкости принимаем равной нулю, W₁ =0 ) и 22 (рис. 41а) :

(6.4)

• Потери давления в насадке складываются из потерь на входе и на внезапное расширение струй внутри насадка

Т.к

• ,

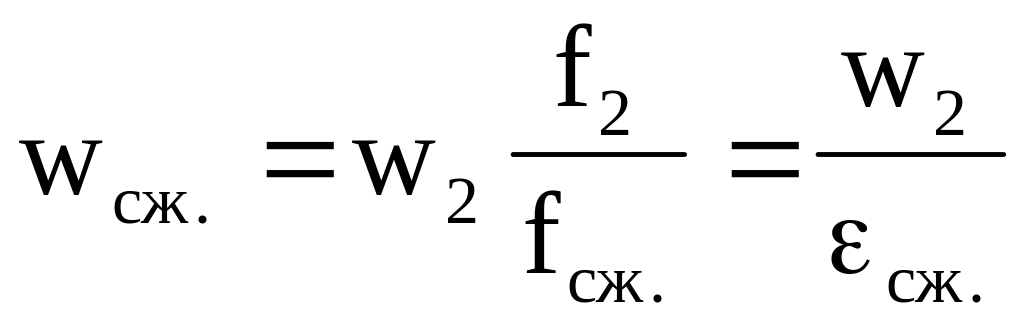то

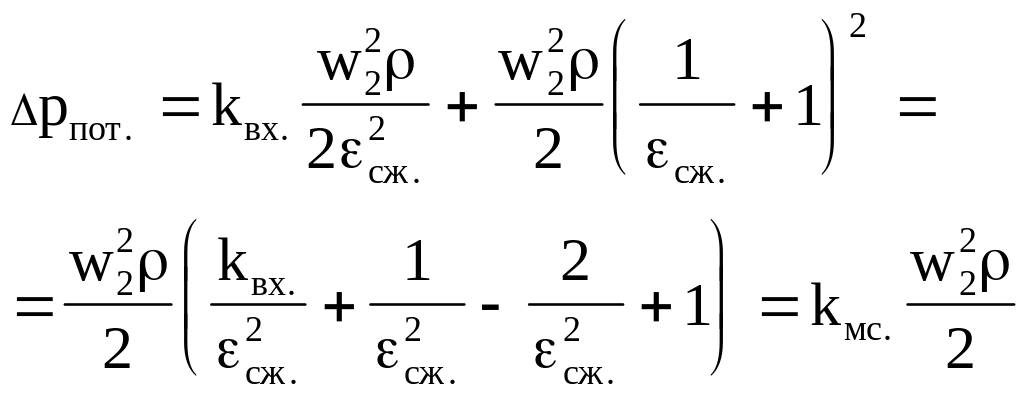(6.5)

Теперь уравнение запишется в виде:

• 

а скорость истечения

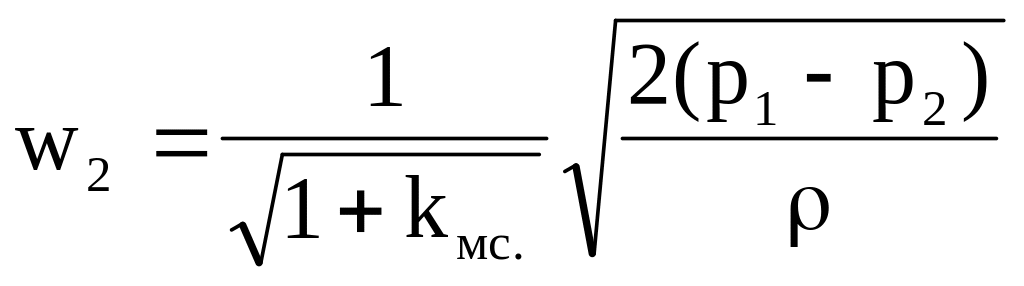(6.6)

или

• 

где

• ,

• 

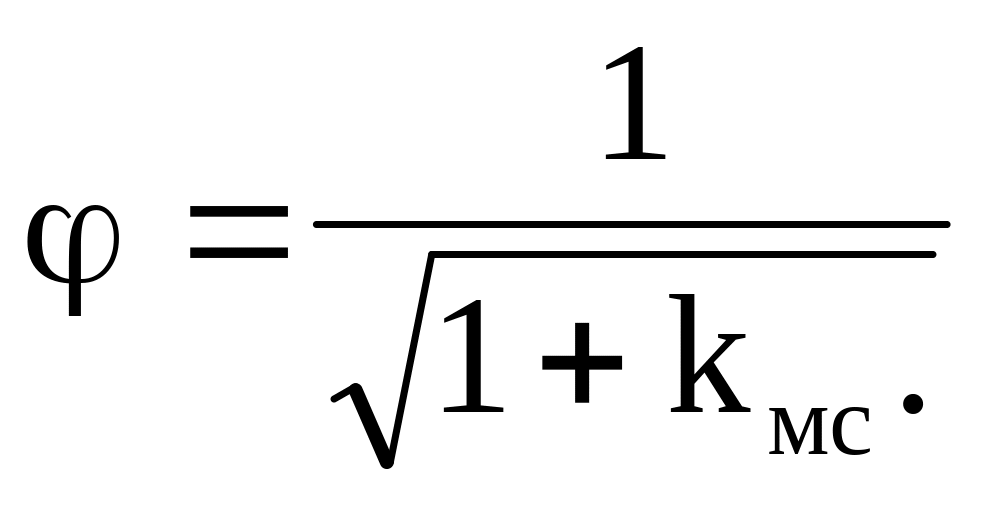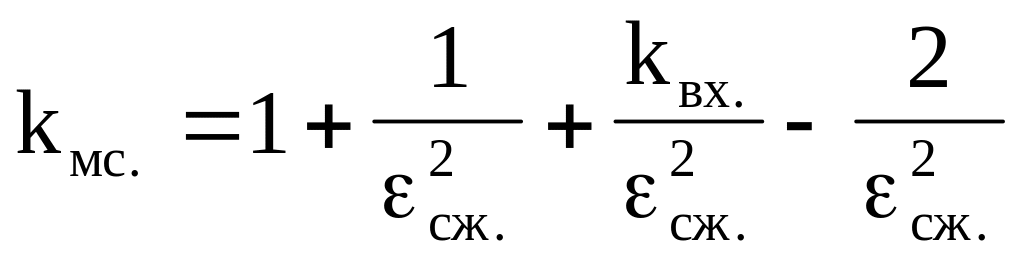
и при значениях k_вх=0,04...0,06 и _сж=0,63 =0,82...0,85.

• В случае, если цилиндрический насадок имеет плавный вход (рисунок 6.2, б), то сопротивление насадка значительно снижается и коэффициенты, скорости и расхода близки к единице: ==0,95...1,0. Если же к отверстию приставить конический расходящийся насадок (диффузор) с плавными кромками у входа (рисунок 6.2, в), то коэффициент расхода становится больше единицы и для наиболее выгодных углов конусности  =7...12° и =1,1...l,2, если в формуле

• 

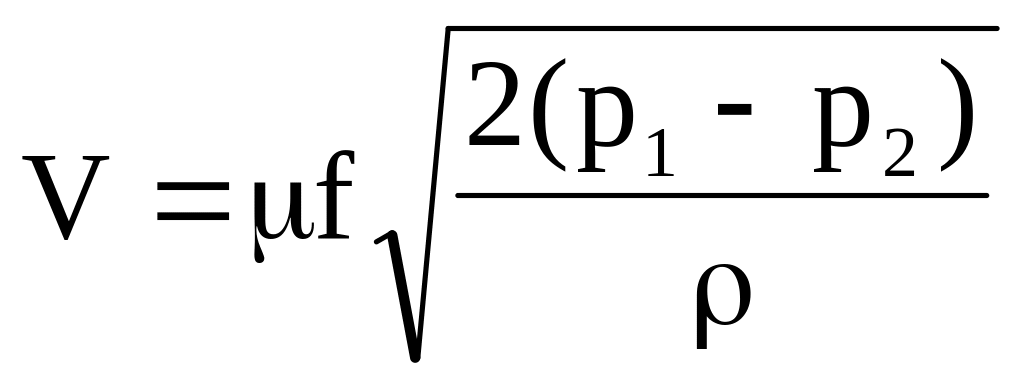
в качестве расчетного, принимается сечение на входе, а отношение l/d=3. Если угол конусности  > 12°, то струя отрывается от стенок и коэффициент расхода резко падает. Диффузорный насадок целесообразно применять в тех случаях, когда при заданном давлении p₁ нужно увеличить расход и в то же время уменьшить скорость истечения жидкости (например, желая избежать размыв грунта). Следует заметить, что в насадках в месте сжатия струи создается вакуум (давление меньшее, чем в сечении 22). В диффузорных насадках величина вакуума больше, чем в цилиндрических насадках, поэтому их используют также там, где необходимо достичь значительный всасывающий эффект (инжекторы, эжекторы, струйные насосы).

• Таким образом, применяя насадки можно получить существенное увеличение расхода жидкости по сравнению с простыми отверстиями: для цилиндрического насадка с острыми кромками в 0,82:0,63=1,31 раза, для цилиндрического насадка с плавными кромками в 0,95:0,63=1,51 раза, для диффузорного насадка в 1,2:0,63=1,91 раза.