24.Общие принципы расчета сложных гидравлических систем

В промтеплоэнергетике к сложным системам относятся трубопроводы для подачи воздуха, газообразного и жидкого топлива, воды к паровым котлам или промышленным печам, паропроводы, трубопроводы систем теплоснабжения, дымовые тракты для эвакуации продуктов сгорания, и т.д. В качестве примера рассмотрим систему, схема которой приведена на рис. 5.14. К камере промышленной печи 7 вентилятором 1 через воздушный тракт (В. Т.) подается воздух для сжигания топлива. Воздушный тракт представляет собой последовательно соединенные гидравлические сопротивления (задвижки 2, рекуператор 3, измерительное сужающее устройство 4, регулирующий дроссель 5, несколько резких и плавных поворотов; прямые участки трубопроводов; подъёмы и опускания; истечение воздуха через отверстия в горелке 6 ). Продукты горения удаляются из рабочей камеры печи за счет тяги дымовой трубы 11, причем одна труба может обслуживать одновременно несколько промтеплоэнергетических объектов. Например, как показано на рис. 39 к дымовой трубе присоединено параллельно пять дымовых трактов (Д.Т.1...Д.Т.5), причем каждый из этих трактов в свою очередь представляет собой набор последовательно соединенных сопротивлений, Так, рабочую камеру 7 и дымовую трубу 11 соединяет дымовой тракт Д.Т.2, в состав которой входят отсечные шибера 8, рекуператор 9, регулирующая заслонка 10, повороты, опускания, подъёмы и т.п. Показанная в примере система является сложной, т.е. включает большое количество гидравлических сопротивлений разных типов, расположенных как последовательно, так и параллельно.

Рисунок 5.14 - Схема сложной гидравлической системы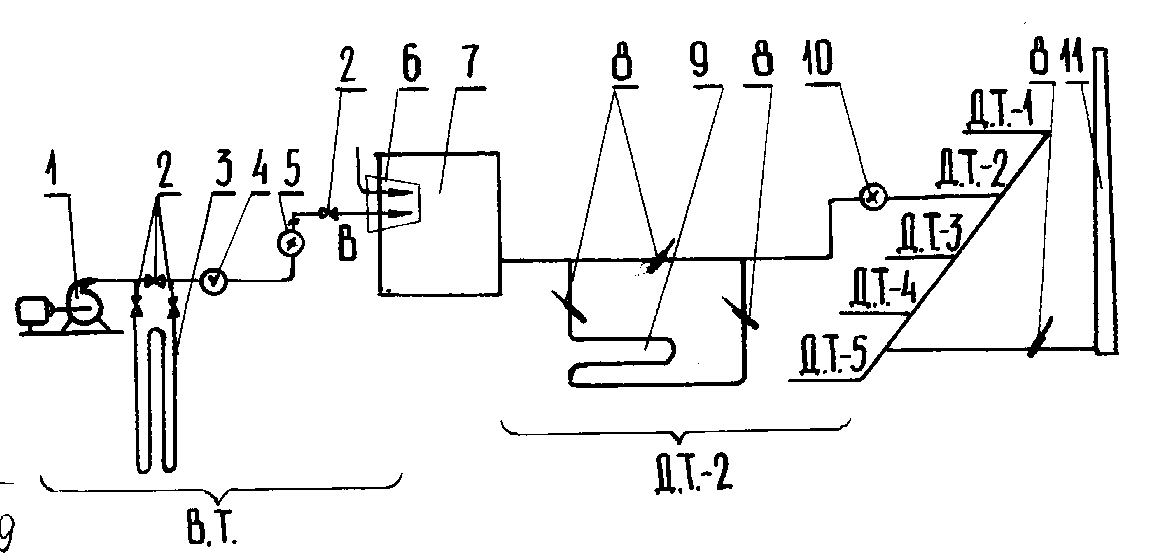

В практике гидравлических расчетов встречаются две постановки задачи.

Первая задача. Задана геометрия всей системы и расход жидкости (газа), необходимое давление в конце нагнетательной системы или в начале отсосной системы. Требуется определить давление на входе нагнетательной системы, которое должен создать нагнетатель (вентилятор, компрессор, насос и др.), и производительность; или требуется определить разрежение на выходе отсосной системы, которое должно создать тяговое (отсасывающее) средство (дымосос, дымовая труба, эксгаустер и др.), и его производительность.

Давление, развиваемое нагнетателем, должно быть не меньше общего расчетного сопротивления системы р_расч с учетом статического давления в рабочей камере р и динамических давлений на входе и выходе нагнетательной системы ( ):

, (5.22)

Расчетное сопротивление системы

, (5.23)

где  максимальное из суммарных сопротивлений параллельных трактов (суммирование сопротивлений всех параллельных трактов является грубой ошибкой, приводящей к завышению мощности нагнетательного или отсасывающего средства);

 суммарное сопротивление общей части системы (до или после разветвления);

k_зап  коэффициент запаса, учитывающий возможное форсирование работы промтеплоэнергетической установки, а также засорение тракта в процессе эксплуатации; k_зап=1,3...1,5.

Суммарное сопротивление p или p представляет собой сумму всех потерь на трение, местные сопротивления и потерь геометрического давления:

. (5.24)

где k_вв  коэффициент, учитывающий взаимное влияние местных сопротивлений (см. раздел 5.6).

Производительность нагнетателя должна быть не меньше суммарного расхода жидкости по вcем параллельным трактам с учетом запаса:

, м³/с (5.25)

где V_i  расход жидкости через iтый тракт;

n  количество параллельных трактов в системе;

k_з=1,1...1,2  коэффициент запаса, учитывающий возможное форсирование промтеплоэнергетической установки.

Вторая задача. Задана геометрия всей системы и давление (разрежение) на входе и выходе. Требуется найти пропускную способность системы, под которой подразумевается расход жидкости.

Рассмотрим решение этой задачи на примере относительно простой системы, состоящей из последовательно соединенных сопротивлений, при движении несжимаемой жидкости. Величина расхода жидкости влияет на значение потерь давления на трение и местные сопротивления, т.к. в формулы для их расчета входят средние по сечению скорости, которые пропорциональны расходу. Потери в i том местном сопротивлении рассчитываются по формуле:

.

Т.к. w_i=V/F_i, то

, (5.26)

где F_i  расчетное поперечное сечение для i  того сопротивления. Аналогично для потерь на трение

(5.27)

Заданная по постановке задачи разница давлений на концах системы будет израсходована на преодоление сопротивления системы, т.е. р_н  р_к = р_.

Тогда, подставляя (5.26),(5.27) в (5.24), получим :

, (5.28)

откуда и определяется пропускная способность системы V. (Заметим, что после получения результата в первом приближении иногда требуется корректировка расчета, связанная с необходимостью уточнения коэффициента трения _i, зависящего от числа Рейнольдса).

Для сложной системы, состоящей из параллельно соединенных последовательно сложных систем, для определения пропускной способности составляют и решают систему уравнений типа (5.28).