19.2. Потери на трение в потоке сжимаемых жидкостей (газов высокого давления)

При движении несжимаемых жидкостей (на практике  это чаще всего газы высокого давления) давление по длине трубопровода уменьшается вследствие потерь энергии на перемещение газа, при этом увеличивается удельный объем газа и снижается плотность. Поэтому формула (5.7) для расчета потерь на трение не пригодна. На участке газопровода высокого давления длиной l (рисунок. 5.1) потери на трение p = p_н  p_к. Ниже приводится вывод уравнения для расчета конечного давления р_к.

Рисунок 5.1. Потери на трение в газопроводе высокого давления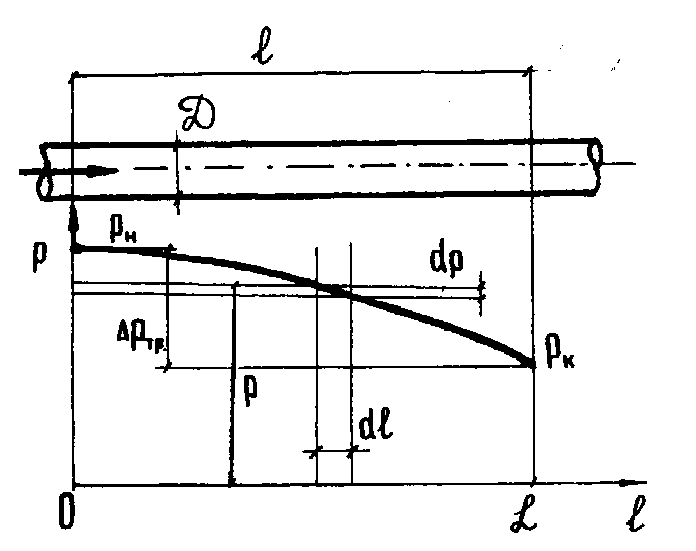

Изменение давления на элементарной длине dl равно

,

т.к. плотность газа на элементарном отрезке dl можно принять величиной постоянной. Для интегрирования этого выражения сделаем подстановки:

• .

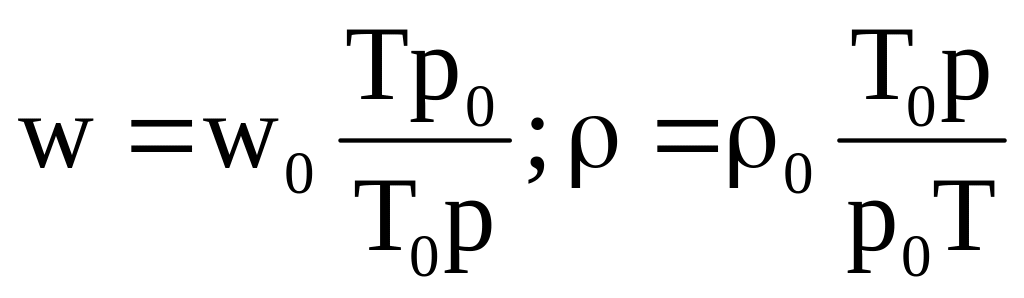После подстановки и разделения переменных получим

• 

интегрируя по р от р_н до р_к и по l от 0 до L получим:

• 

и окончательные выражения для расчета давления в конце участка длиной L:

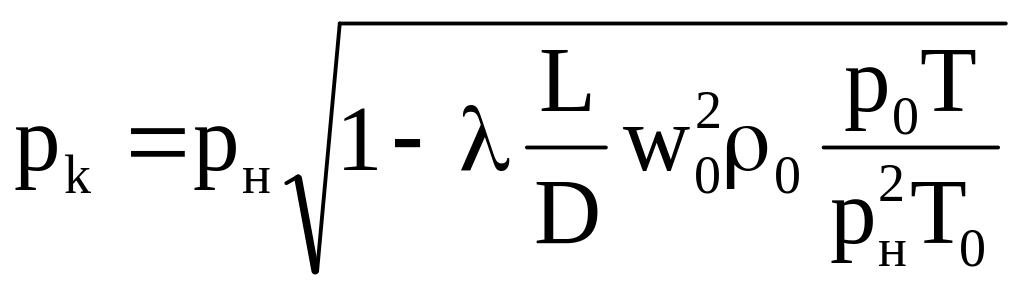• , (5.9)

и потерь давления на трение:

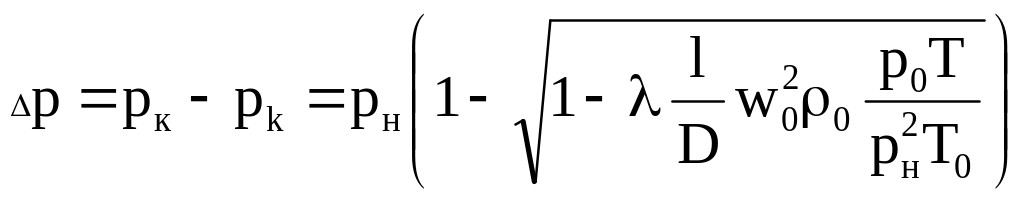• . (5.10)

В формулах (5.9) и (5.10) приняты следующие обозначения и размерности: р_н и p_к.  абсолютное давление в начале и конце участка Па; L  длина участка, м; D  диаметр трубопровода, м; w₀, ₀  скорость и плотность газа при н.ф.у., м/с, кг/м³; р₀=101300 Па; Т₀= 273 К; Т температура газа, К.

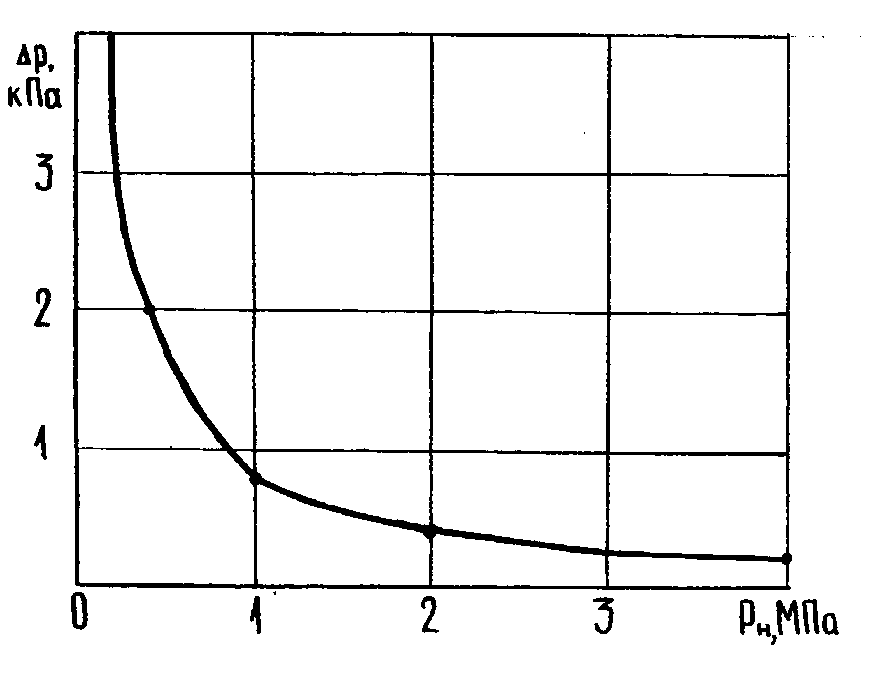
Исследуем влияние начального давления р_н на потери энергии при одинаковом массовом расходе и скорости газа (w₀=const) на следующем примере. По газопроводу диаметром D = 1 м длиной 1000 м движется газ со скоростью w₀=40 м/с; плотность газа ₀=1кг/м³, температура Т= 273 К; коэффициент трения = 0,01.

Таблица 5.1  Потери давления при различном начальном давлении газа

pн,106 Па	A/pн2	1A/pн2		1	p,Па
1,2	4102	0,9600	0,9800	0,0200	4000
0,4	1102	0,9900	0,9950	0,0050	2000
1,0	1,6103	0,9984	0,9992	0,0008	800
2,0	4104	0,9996	0,9998	0,0002	400
4,0	1104	0,9999	0,99995	0,00005	200

• Требуется рассчитать потери давления для различных вариантов начального давления р_н : 0,2; 0,4; 1,0; 2,0 и 4 МПа. Запишем выражение (5.10) в виде:

• ,

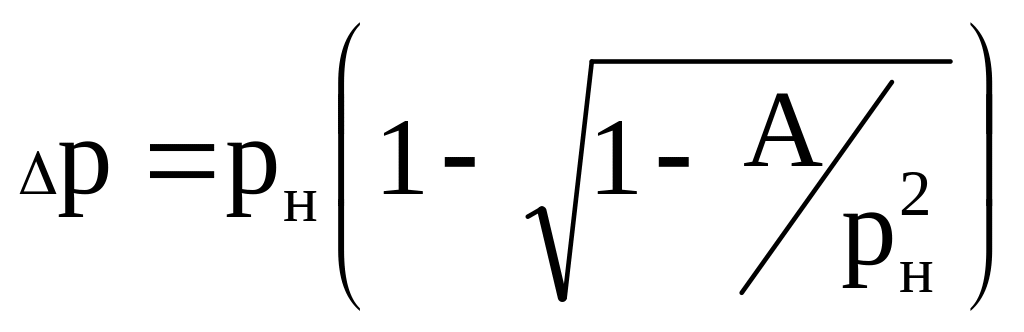• где коэффициент А является постоянной величиной во всех вариантах:

• .

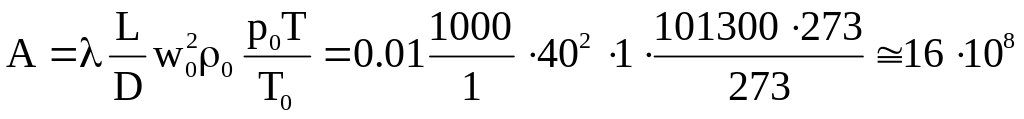Результаты расчета сведем в табл. 2 и представим в виде графика (рис. 5.2), из которого видно, что чем больше давление, тем меньше потери энергии. Следовательно, чем выше давление газа, тем дешевле обходится транспортировка одного и того же количества газа.

• 

19.3. Рисунок 5.2 Зависимость потерь давления от начального давления газа Коэффициент трения

Значение коэффициента трения  зависит от режима течения, состояния внутренней поверхности стенки трубопровода, диаметра канала.

При ламинарном течении ( Rе < 2300, lgRe = 3,4) коэффициент трения определяется по формуле Пуазейля:

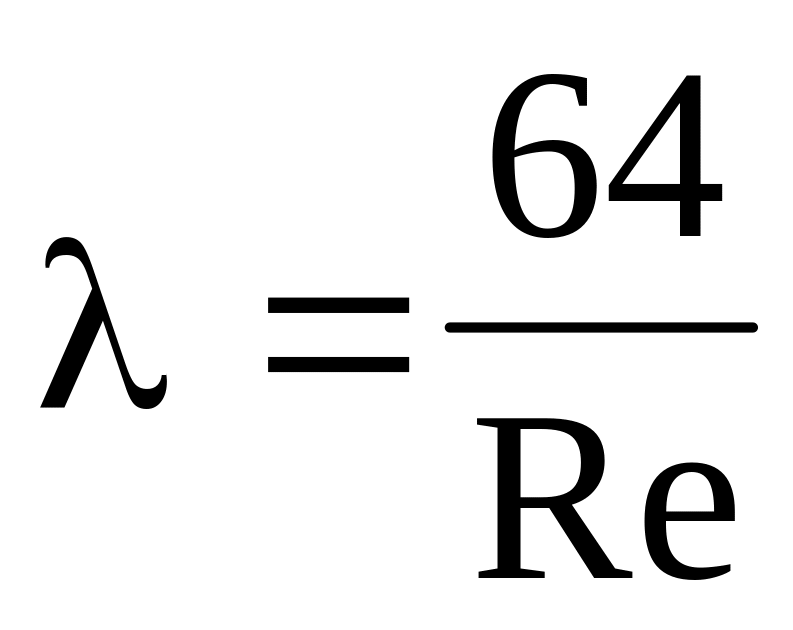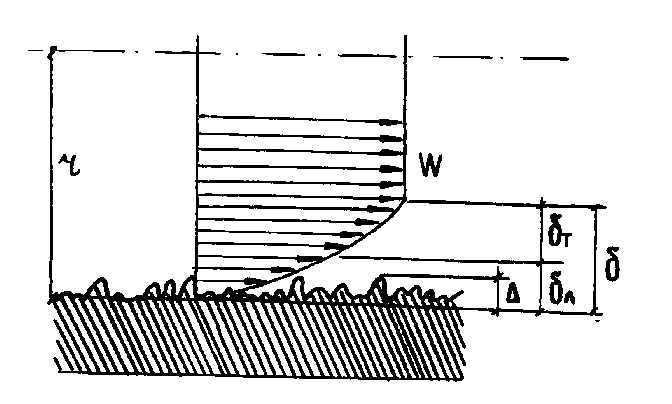
• . (5.11)

• При турбулентном движении способ определения зависит прежде всего от того, происходит движение жидкости в «гидравлически гладкой» или «гидравлически шероховатой» трубе. При движении турбулентного потока вдоль поверхности возникает переходная зона, или пограничный слой толщиной , в котором скорость падает от w до нуля, причем =_л+_т, где _т  толщина турбулентного подслоя, _л  толщина ламинарного подслоя. Величина _л определяется по эмпирической формуле

• • 

  Рисунок 5.3 Пограничный слой и шероховатость

   = 68,4  Re ^0.875 r, м (5.12)

Если абсолютная шероховатость, или высота выступов  (рисунок 5.3) меньше, чем _л, то труба считается гидравлически гладкой (ламинарный подслой в этом случае выполняет роль смазки), то коэффициент трения определяется по эмпирической формуле Блазиуса:

=0,316Re ^0,25 (5.13)

Если >_л, то выступы шероховатости проникают в турбулентное ядро потока, а труба называется гидравлически шероховатой. Коэффициент трения в этом случае не зависит от числа Рейнольдса и определяется в зависимости от шероховатости по эм пирической формуле Никурадзе

=(2lg(r/)+1,74)^2 , (5.14)

или по формуле Шифринсона

=0,11(/2d)^0,25 (5.15)

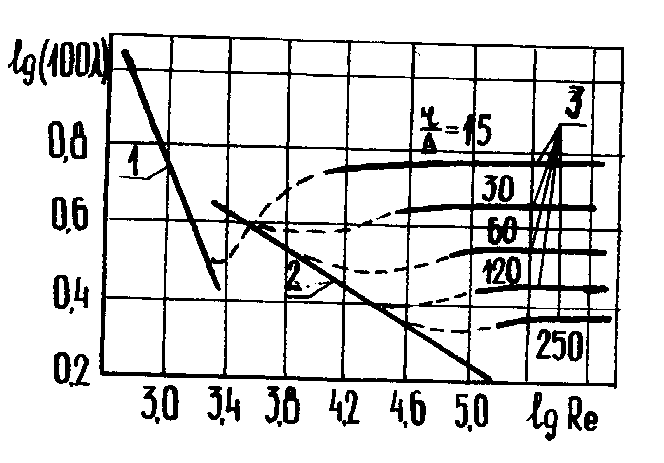Зависимость коэффициента трения от числа Рейнольдса и шероховатости систематизирована в опытах И. Никурадзе (1933 г.) и представлена на рис. 5.4. Прямая 1 соответствует ламинарному режиму течения и формуле (5.11), когда  не зависит от шероховатости трубы и обратно пропорциональна числу Рейнольдса. Прямая 2 соответствует течению в гидравлически гладкой трубе и формуле (5.13), когда  также не зависит от шероховатости и уменьшается при увеличении Рейнольдса. Серия прямых 3 соответствует течению в гидравлически шероховатой трубе и формуле (5.14), когда  не зависит от числа Рейнольдса и определяется только относительной шероховатостью /r: чем больше последняя величина, тем выше расположена соответствующая кривая и тем меньше число Рейнольдса, при котором происходит переход к режиму течения в шероховатой трубе. Значения абсолютной шероховатости  приводится в справочниках. В табл.5.2 приведена шероховатость для некоторых случаев.

Рисунок 5.4. График Никурадзе

Таблица 5.2  Значения эквивалентной абсолютной шероховатости  для труб из различных материалов

Труба, канал	Состояние поверхности	, мм
Тянутые из стекла или цветных металлов	Новые, технически гладкие	0,001
Стальные сварные	новые и чистые	0,06
	умеренно заржавевшие	0,5
	сильно заржавевшие, с отложениями	3
Чугунные	новые	0,3
	бывшие в употреблении	1
Бетонные, кирпичные	новые центробежные	0,2
	из необработанного бетона, кирпичные	2

В технических расчетах часто принимают (с некоторым запасом) ориентировочные значения коэффициентов трения; для металлических труб =0,02...0,03, для кирпичных и бетонных каналов =0,04...0,05.