4 Динамика. Основные уравнения
Предметом
раздела гидрогазодинамики
динамики
является изучение движения жидкостей
в связи с их взаимодействиями, т.е.
изучаетcя не только
геометрия движения, но и причины,
вызвавшие его.
13.Дифференциальное уравнение движения несжимаемой идеальной (невязкой) жидкости (уравнение движения Эйлера)
Для вывода уравнения применим основной принцип механики: тело находится в состоянии движения, если сумма проекций всех сил, действующих на тело, равна произведению массы движущегося тела на его ускорение:
.
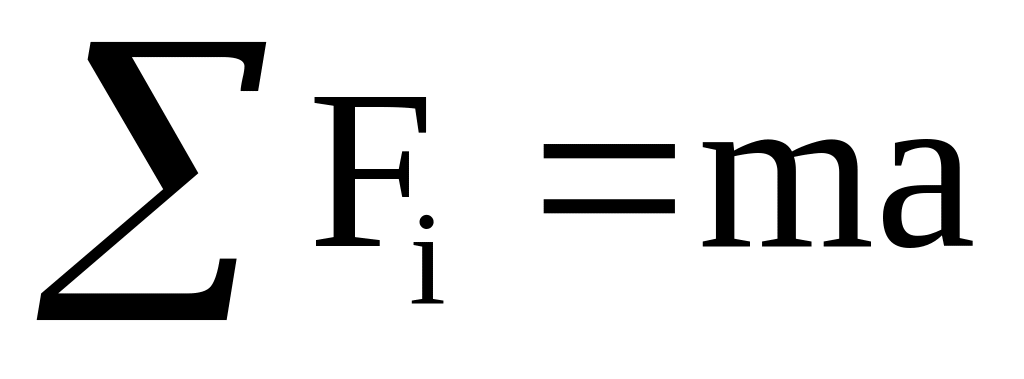Как и при выводе уравнений равновесия Эйлера рассмотрим действующие на элементарный объем жидкости dxdydz массовые силы с вектором ускорения G(Х,У,Z) и поверхностные (давления). Сумма этих сил должна быть равна силе инерции. Для проекции на ось х:
.
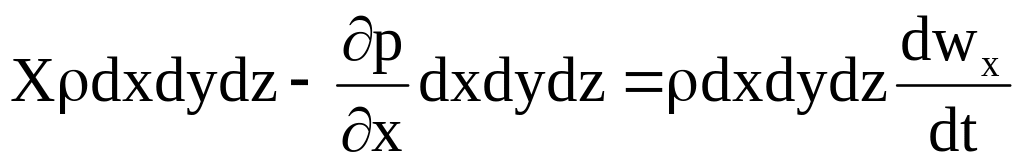Аналогично для проекций сил на другие оси. После упрощений получим систему уравнений:
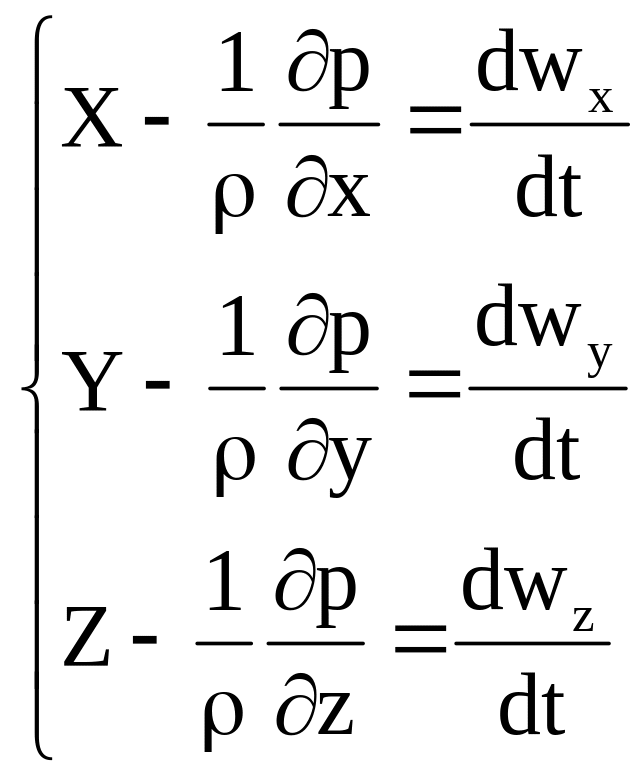. (4.1)
Полученные уравнения называются системой уравнений движения Эйлера. В векторной форме:
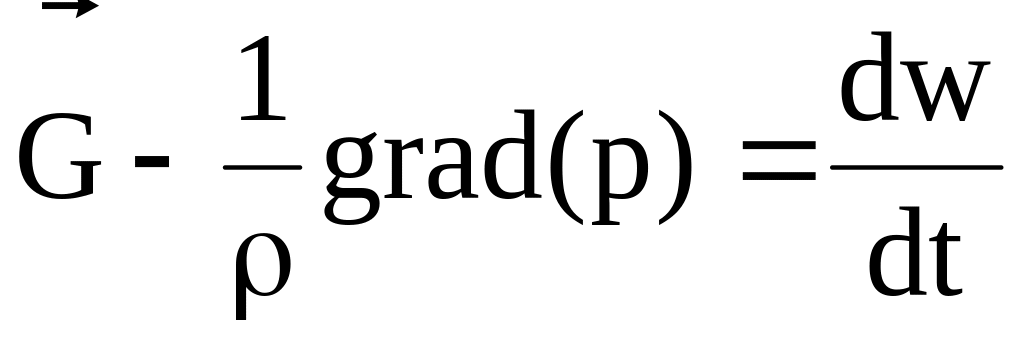, (4.2)
или
.
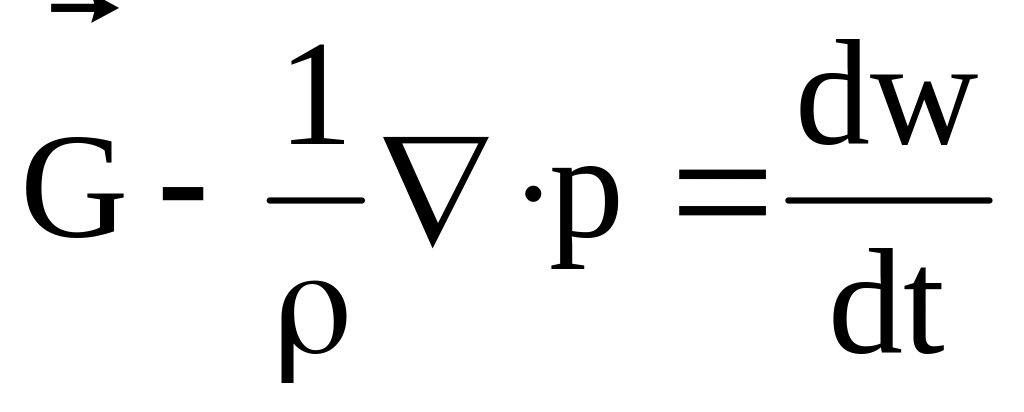(4.3)
Следует напомнить, что правые части уравнений являются полными или субстанциальными производными:
.
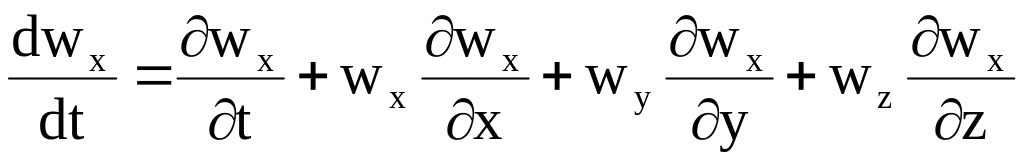14.Дифференциальное уравнение движения несжимаемой реальной (вязкой ) жидкости (уравнение Навье-Стокса)
В движущейся реальной (вязкой) несжимаемой жидкости помимо массовых сил, поверхностных сил (давления) и сил инерции действуют также силы внутреннего трения. Касательные напряжения этих сил описываются, как указывалось ранее, уравнением Ньютона:
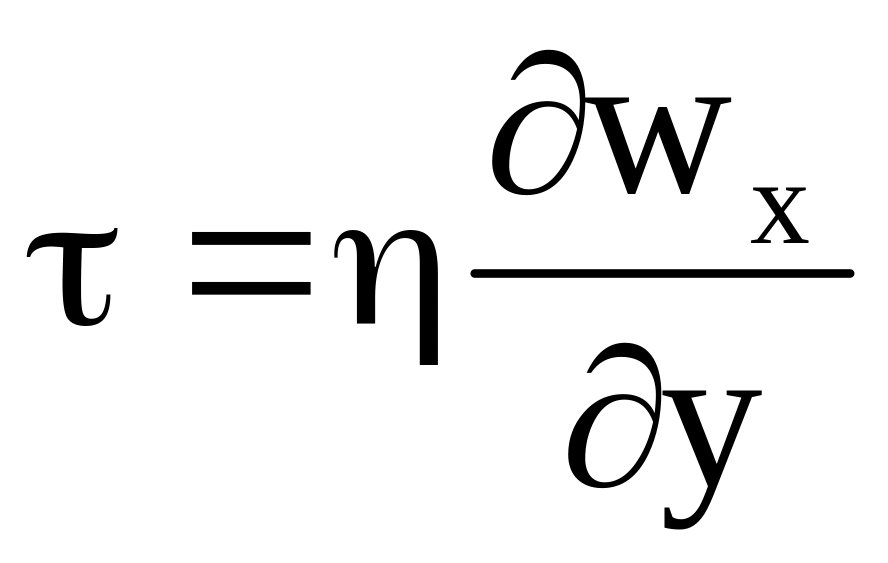.Рассмотрим случай простейшего плоскопараллельного одномерного движения в направлении координатной оси x (рисунок 4.1), при этом скорость изменяется только в направлении оси y. Выделим в движущейся жидкости элементарный объем dxdydz. Около нижней грани касательное напряжение силы внутреннего трения направлено против движения, т.к. скорость частиц здесь меньше, чем в самом выделенном элементе. Около верхней грани скорость частиц больше, чем в элементе, поэтому сила внутреннего трения здесь направлена в обратную сторону, напряжение внутреннего трения здесь отличается на приращение d, равное произведению градиента напряжения на длину dy:
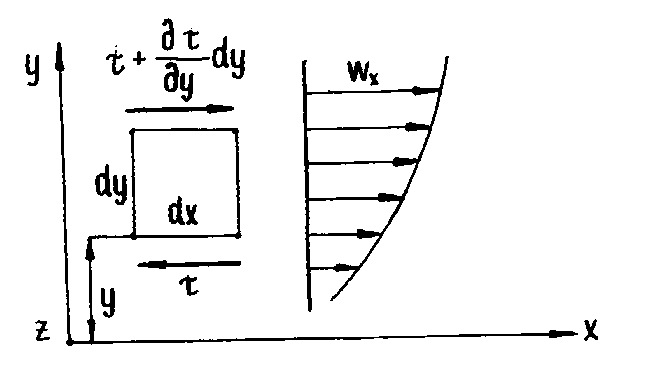
Рисунок 4.1 К выводу уравнения Навье-Стокса
.
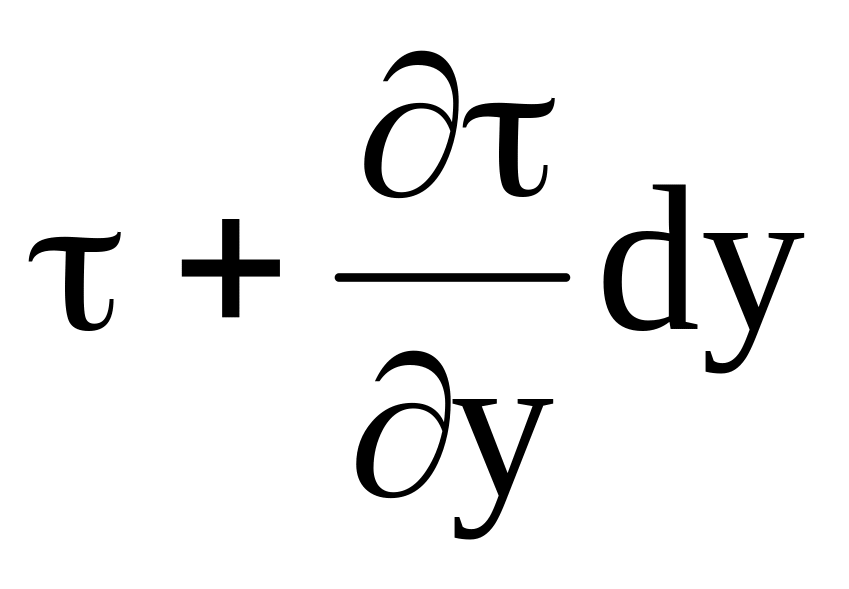Произведение напряжения на поверхность dxdz это сила внутреннего трения, а равнодействующая сил, действующих на верхнюю и нижние грани, равна их алгебраической сумме:
или
.
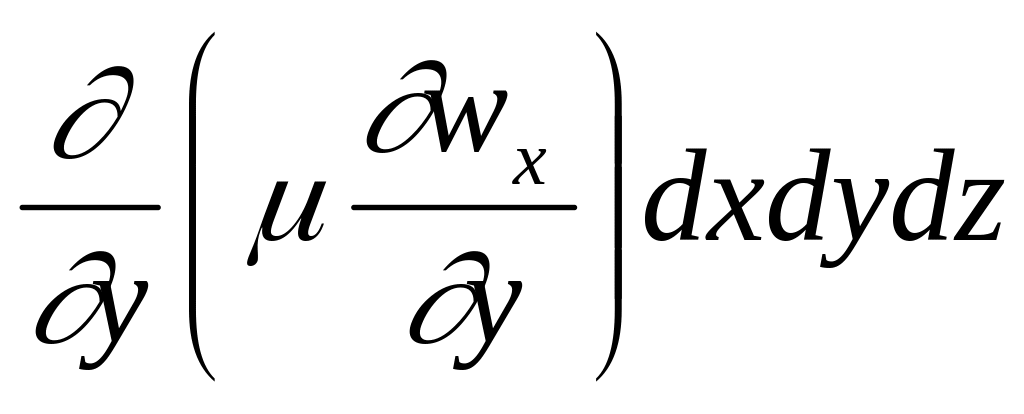После деления на массу элементарного объема dxdydz и введения замены p= получим выражение для ускорения силы внутреннего трения:
.
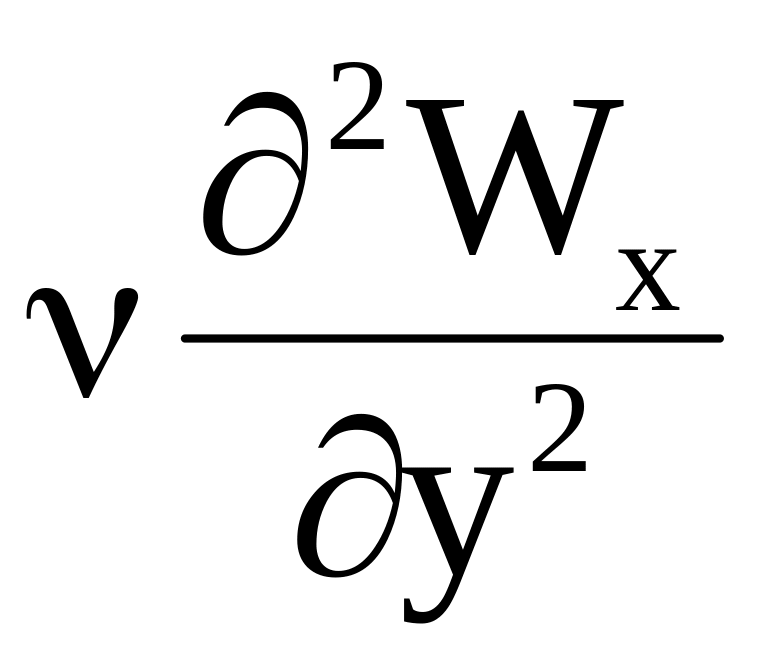Если в общем случае рассмотрим трехмерное движение и добавим в уравнения движения Эйлера (4.1) ускорения сил внутреннего трения, то получим систему дифференциальных уравнений, называемых уравнениями Навье-Стокса:
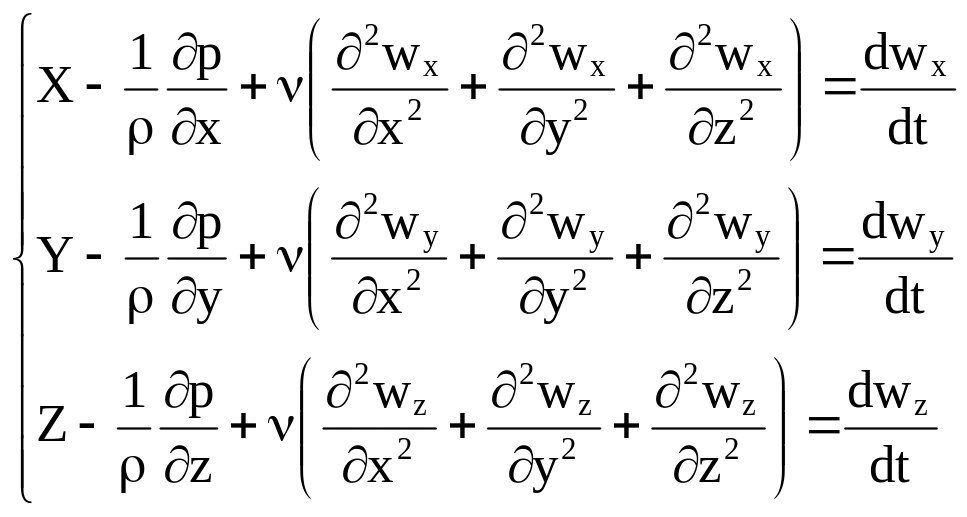, (4.4)
или в векторной форме
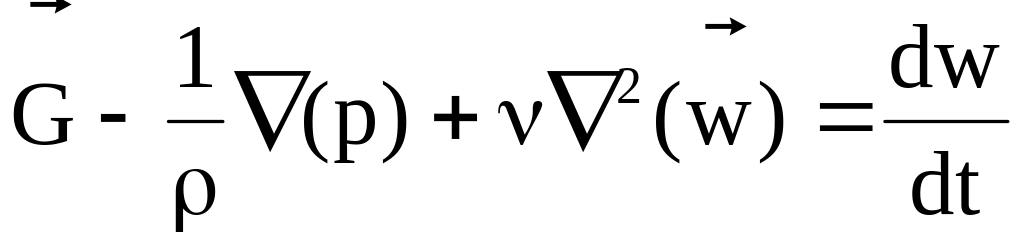, (4.5)
где 
оператор Лапласа.
Следует помнить, что в правой части уравнении стоят полные, или субстанциальные производные.
15.Уравнение Навье-Стокса для сжимаемой жидкости
В случае движения сжимаемой вязкой жидкости в уравнении движения должна быть отображена сила внутреннего трения, обусловленная сдвигом слоев вследствие объемной деформации (сжатия или растяжения) жидкости. Уравнение Навье-Стокса в этом случае будет иметь вид (без вывода):
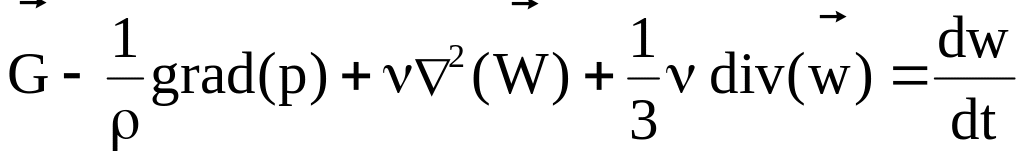(4.6)
Это уравнение является наиболее общим, а все другие ранее полученные уравнения: уравнение Навье-Стокса для несжимаемой жидкости (4.5), уравнение движения Эйлера (4.2), уравнение равновесия Эйлера (2.2) его частными случаями.
Общее решение уравнений Навье-Стокса, которые являются нелинейными дифференциальными уравнениями второго порядка в частных производных, до сих пор не найдено. В нахождении общего решения большая роль в настоящее время отводится приближенным численным методам, в частности, таким, как метод конечных элементов, метод граничных элементов, метод контрольных объемов. Не имея пока общего решения, можно получить ряд практически важных частных решений, вводя различные упрощения. Одна из целей первичного курса гидрогазодинамики развить «чутье» к выбору надлежащего приближения для решения той или иной инженерной задачи.