11. Уравнение неразрывности или сплошности (Уравнение расхода)

Уравнение неразрывности (сплошности) отображает закон сохранения массы в движущейся жидкости. Принцип сохранения массы для любой определенной системы:

(Чистый приток массы в систему) = (Приращение массы системы)

Выделим в движущейся жидкости элементарный контрольный объем в форме параллелепипеда со сторонами dx, dy, dz (рисунок 3.6), в котором отсутствуют источники (стоки), а плотность и скорость являются функциями пространственных координат и времени. Массовая скорость потока через левую грань равна w_x; если принять изменение скорости на элементарном участке dx линейным, то приращение скорости на этом участке равно произведению градиента скорости на dx; а значение скорости на противоположной правой грани равно

• .

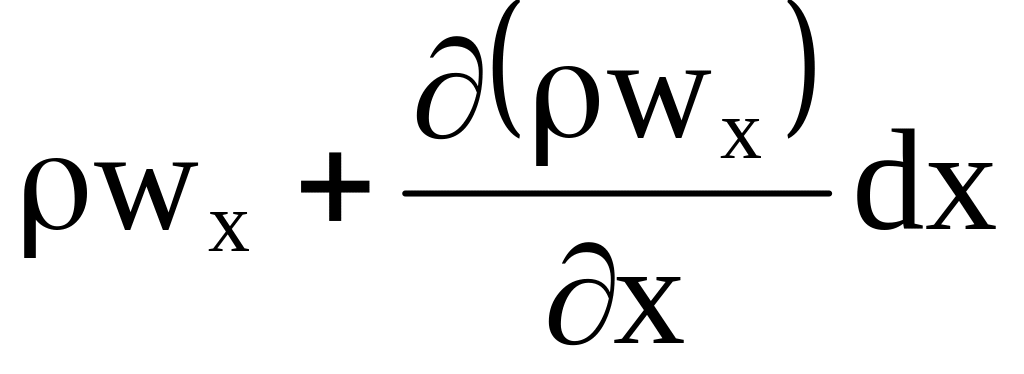Рисунок 3.6. К выводу уравнения неразрывности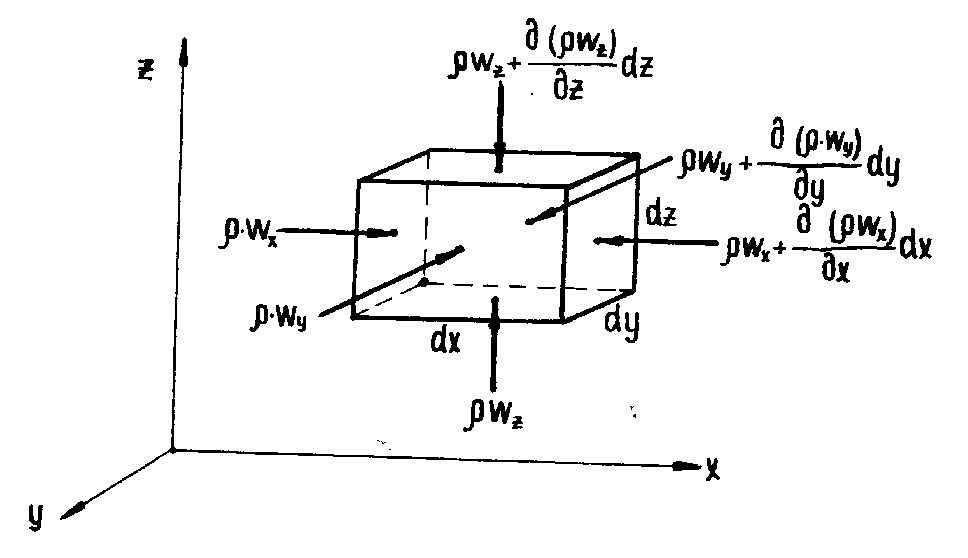

Аналогично записываются значения массовых скоростей на остальных гранях.

Вычислим чистый приток массы в контрольный объем. Количество жидкости, вытекающей в объем за время dt:

• .

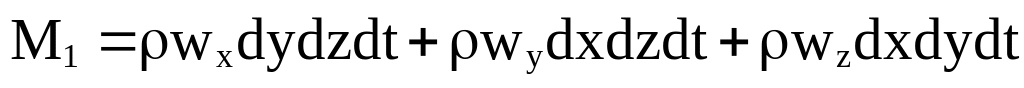Количество жидкости, вытекающей их объема за время dt:

• 

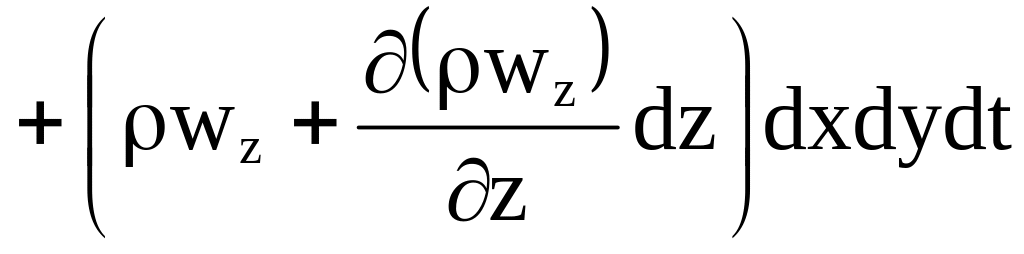
• Изменение массы жидкости в объеме (чистый приток)

• 

• 

• 

• .

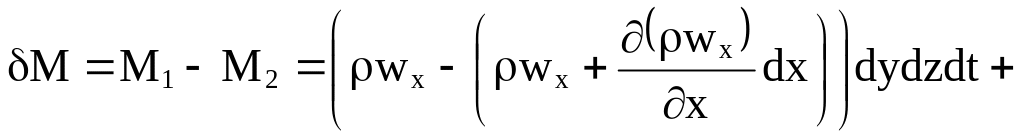
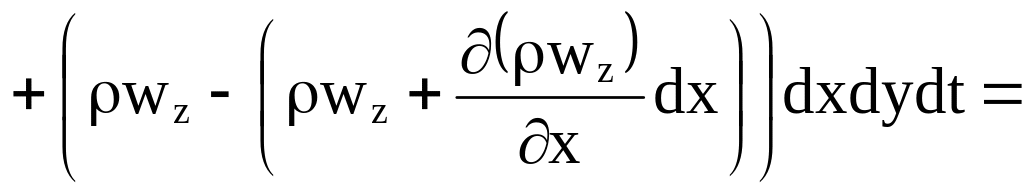
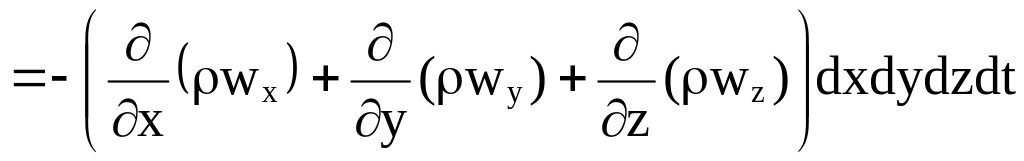Но если в контрольном объеме произошло изменение массы, то это должно сопровождаться изменением плотности

• ,

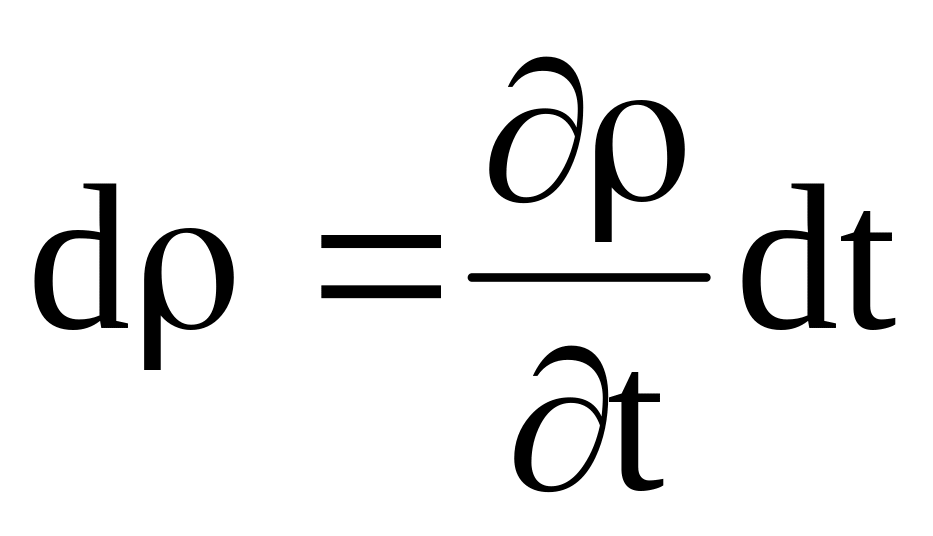а приращение массы равно произведению приращения плотности на объем:

• .

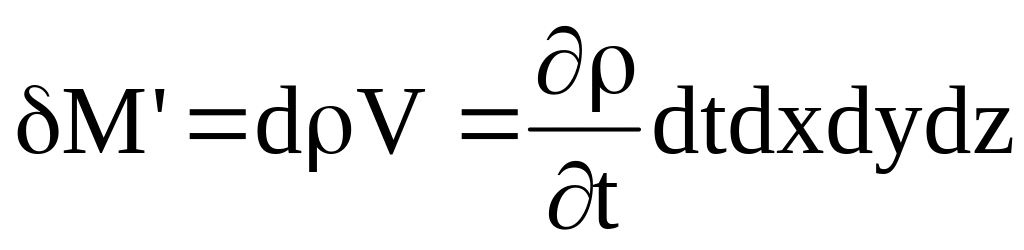Приравнивая М и М, получим

• ,

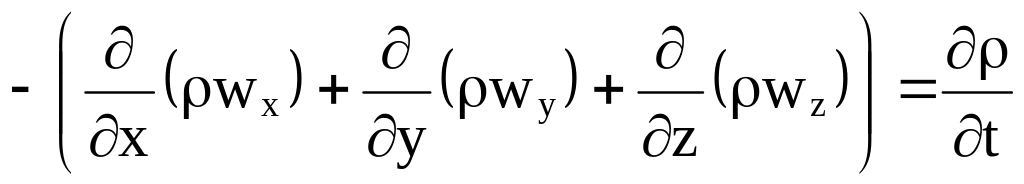и ли

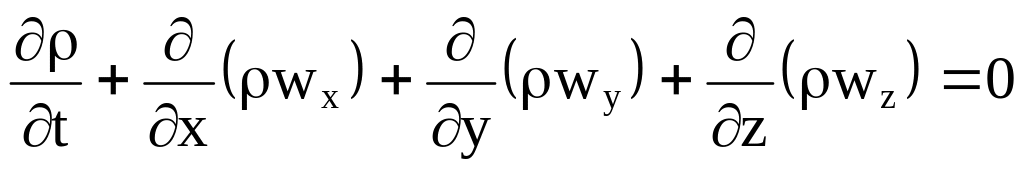• (3.12)

Полученное уравнение является уравнением неразрывности (сплошности) для сжимаемой жидкости при нестационарном течении.

Запись уравнения неразрывности в векторной форме имеет вид

• (3.13)

Скалярное произведение оператора Гамильтона на вектор массовой скорости (W) является скалярной величиной и называется дивергенцией (расхождением) скорости.

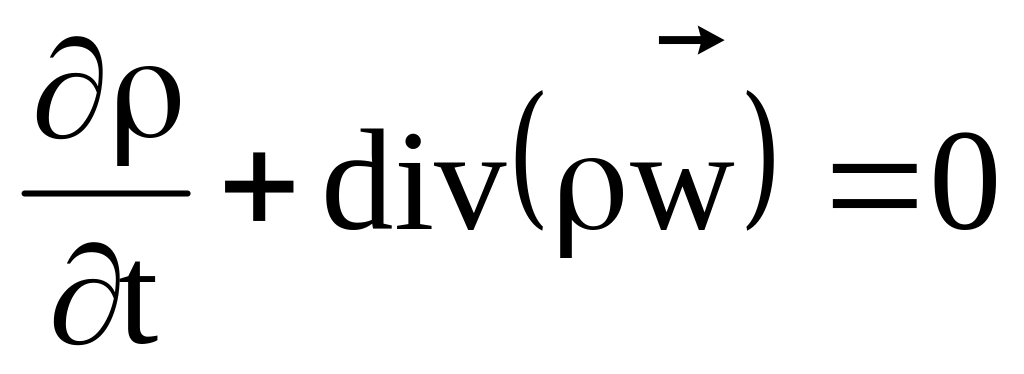• (3.14)

Для стационарного течения , и тогда уравнение неразрывности примет вид

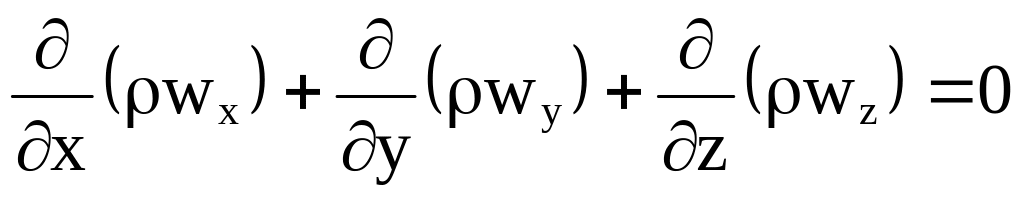• , (3.15)

или

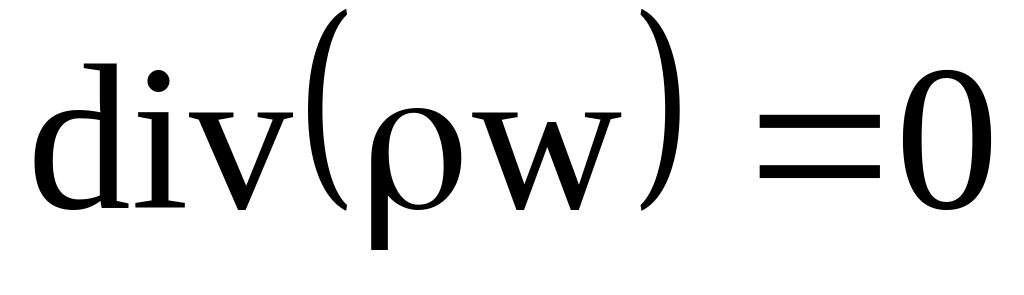• . (3.16)

Для несжимаемой жидкости =const, и тогда

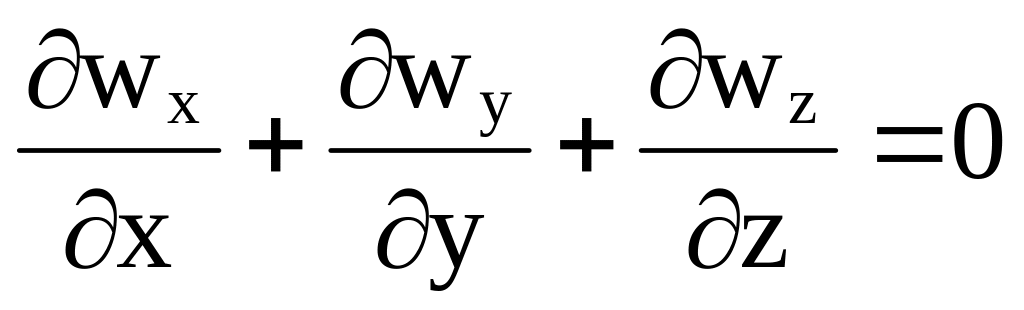• , (3.17)

или

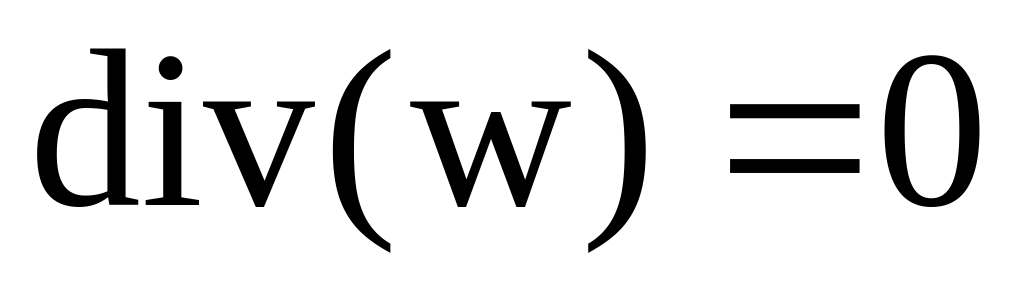• . (3.18)

Для одномерного стационарного движения

• , (3.19)

Интегрируя это соотношение для трубки тока переменного сечения от сечения 1 (площадь поперечного сечения F₁) до сечения 2 (F₂), получим

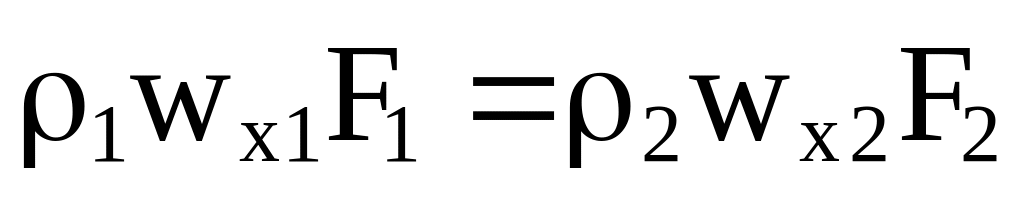• . (3.20)

Последнее выражение является уравнением неразрывности для трубки тока. Для движения в трубах и каналах это уравнение также применимо, если локальную скорость заменить на среднюю по сечению:

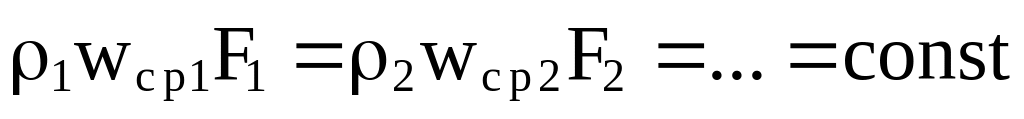• . (3.21 )

Теперь это уравнение характеризует постоянство массового расхода жидкости в любом сечении трубопровода. Для несжимаемой жидкости (=const)

• . (3.22)

12.Вихревое и безвихревое движение

Вихревым называют движение, при котором частицы жидкости вращаются вокруг собственных осей; если такого вращения нет, то движение называют потенциальным. При рассмотрении вихревого движения вводятся понятия «вихревой линии», «вихревого шнура», «вихревой трубки», которые аналогичны понятиям линия тока, элементарная струйка, трубка тока.

Вихревое движение характеризуется общим вихрем вектора скорости, который может быть. определен вектором угловой скорости:

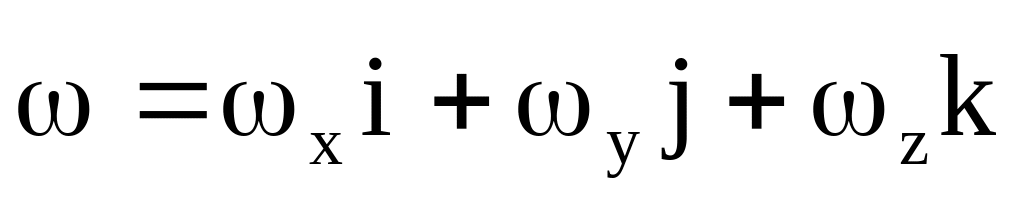• (3.23)

Рассмотрим вращение некоторого тела вокруг оси z с угловой скоростью _z (рис. 3.7). Величина линейной скорости точки М равна произведению _zz, а проекции этой скорости на оси x, y и z  соответственно равны _x = _zy, _y = _zx, _z = 0. Производные

• 

а их разница

• .

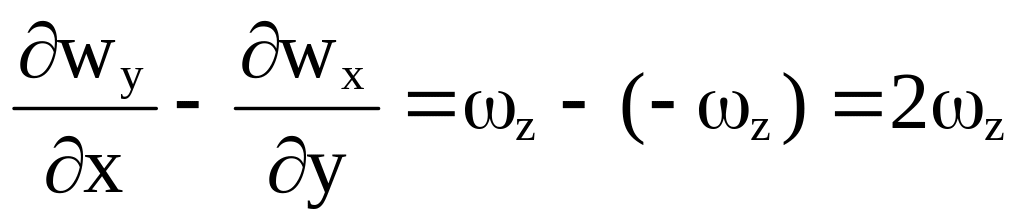Эта разница в соответствии с определениями теории поля является вихрем скорости вокруг оси z, или ротором:

• .

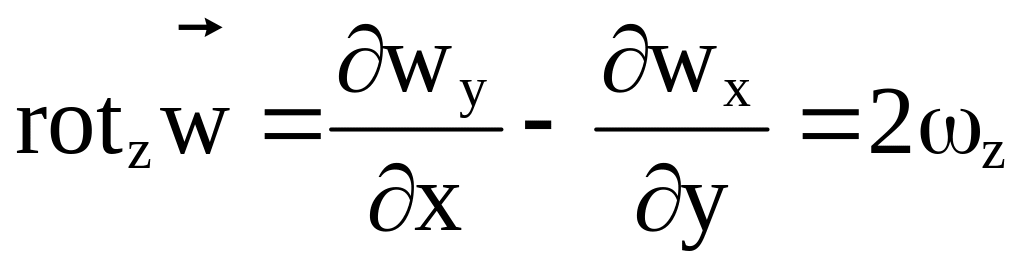Тогда угловая скорость

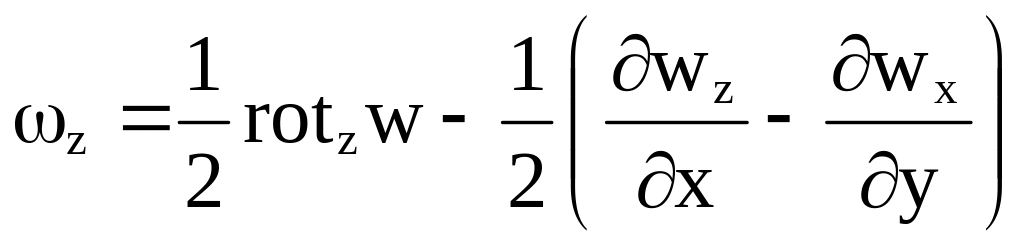• (3.24)

Рисунок 3.7. К выводу вихря вектора скорости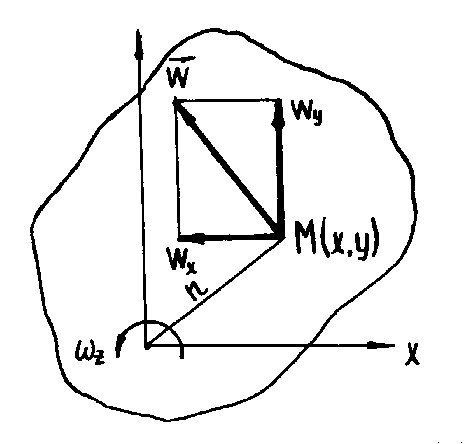

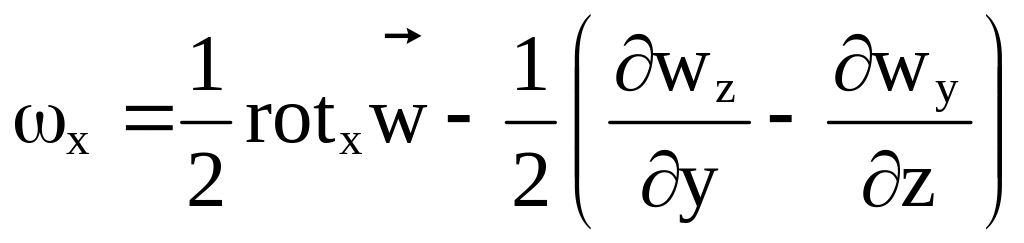Рассмотрев аналогично вращение тела вокруг осей x и у получим

• (3.25)

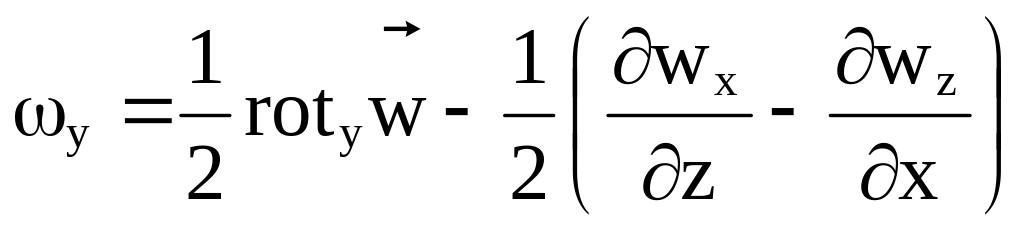• (3.26)

Следовательно, общий вихрь вектора скорости частицы равен:

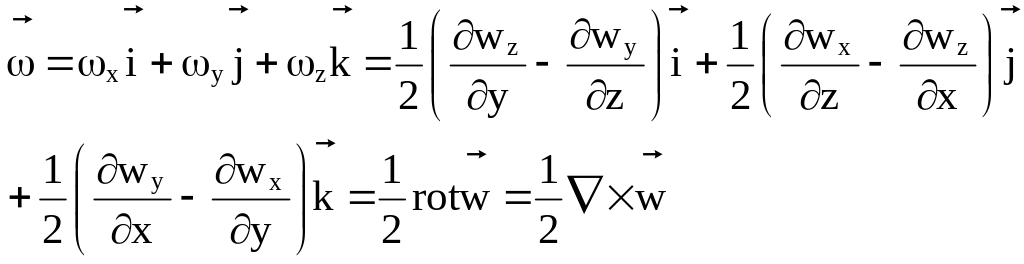(3.27)

Если в какой-либо точке потока, то это означает, что в этой точке имеет место вращение элементарного объема. Если , то течение является безвихревым, или потенциальным.

Теоретическое исследование вихревого движения идеальной жидкости показывает, что вихревые трубки не могут заканчиваться внутри жидкости, они либо замыкаются на себя (кольца табачного дыма), либо опираются на свободную поверхность жидкости или твердого тела (водовороты, смерчи), либо уходят в бесконечность. На практике водовороты не всегда доходят до дна, а вихревые шнуры от крыла самолета сохраняются на конечном расстоянии, что объясняется действием вязкости.

Вихри не образуются внутри области движения: они либо вносятся в нее потоком, либо возникают на границах течения, непроницаемых для жидкости. Источниками завихренности в объектах промышленной теплонергетики являются места, где наблюдаются разрывы скорости, например, при обтекании тел с острыми кромками, кормовая часть шаров или цилиндров (омывание продуктами сгорания трубчатых поверхностей нагрева котлов или рекуператоров; резкие повороты или изменения сечения трубопроводов, и др.). Вихревые области могут быть как вредными, так и полезными. Частицы жидкости, попавшие в вихревую область, долгое время находятся в ней, и в этой области наблюдаются свойства, отличные от остальной массы, например, такие, как температура или концентрация; в этом случае вихревые области нежелательны. В других случаях, например, при истечении газа на срезе сопла горелки возникают вихри, способствующие перемешиванию струй топлива с воздухом, что является полезным.