2. Вопросы и задачи

1. Выбор в условиях неопределенности Верны ли следующие утверждения?

686. Да. Отношение к риску определяется правилами ло­тереи, в которой предстоит участвовать индивиду, и услови­ями, в которых он находится. Функция полезности, как пра­вило, имеет сложный вид и на различных участках характе­ризует индивида как нейтрального к риску, любящего риск и избегающего риск.

687. Да. Так как предельная полезность дополнительной единицы дохода в случае потери будет равняться предельной полезности дополнительной единицы дохода в отсутствие по­тери¹.

688. Нет. Субъективная вероятность формируется на ос­нове информации, которой обладает индивид, а объективная вероятность — на основе статистических расчетов. В некото­рых случаях данные вероятности не совпадают.

689. Да. Так как функция полезности не любящего риск индивида выпукла вверх.

Выберите единственно правильный вариант ответа

686. г. Даны варианты определения данного типа вероят­ности.

687. г. Дисперсия и стандартное отклонение (квадратный корень из дисперсии) являются мерой риска. Чем выше данные показатели, тем рискованней проект.

686. а. Метод снижения риска путем его распределения между рискованными товарами.

687. а. Объединение риска — это метод, направленный на снижение риска путем превращения случайных убытков (сти­хийные бедствия) в относительно небольшие постоянные из­держки (взносы в фонд страхования).

688. г. Представлены различные вариации данного метода.

689. г. Происходит распределение рисков между различ­ными товарами.

Решите задачи и ответьте на вопросы

п

686. Математическое ожидание: Е(х) = => Е(х) =

i=i

= 12 0,2 4- 35 0,25 4- 27 0,35 4- 72 0,15 4- 11 0,05 = 31,95.

п

Дисперсия: а² = ^яДх.-Е(х)]² =>а²= 0,2*[12 - 31,95]²4-

i=i

4- 0,25 [35 - 31,95]² 4- 0,35 [27 - 31,95]² 4- 0,15 [72 - 31,95]² 4­4- 0,05 [11 - 31,95]² = 353,0475.

Стандартное отклонение: D = = 18,79.

686. Из двух проектов более рискованный тот, у которо­го стандартное отклонение больше. Следовательно, необходи­мо найти и сравнить стандартные отклонения обоих проектов.

Для 1-го проекта:

математическое ожидание: Е(х) = 34 0,9 4- 68 0,46 4­4-37 0,08 4- 25 0,03 + 89 0,34 = 68,31;

дисперсия: с² = 0,2 [12 - 31,95]² 4- 0,25 [35 - 31,95]² 4­+ 0,35 [27 - 31,95]² 4- 0,15 • [72 - 31,95]² 4- 0,05 [11 - 31,95]² = = 386,2339.

Стандартное отклонение: D_г = 19,65.

Для 2-го проекта:

математическое ожидание: Е(х) = 18 0,22 4- 13-0,25 4­4- 22 0,2 4- 17 0,18 4- 11 0,15 = 16,32.

дисперсия: а² = 0,2[12 - 31,95]² 4- 0,25 (35 - 31,95]² 4­4- 0,35 [27 - 31,95]² 4- 0,15 [72 - 31,95]² 4- 0,05 [11 - 31,95]² = 14,1576.

Стандартное отклонение: D₂ = 3,76.

Dj > D₂ => Первый проект более рискованный, чем вто­рой.

686. Е(х) = =>Я(х) = 0-0,495 + 10-0,495 + 100-0,009 +

1=1

+ 1000 0,001= 6,85.

686. См. рис. 12.1.

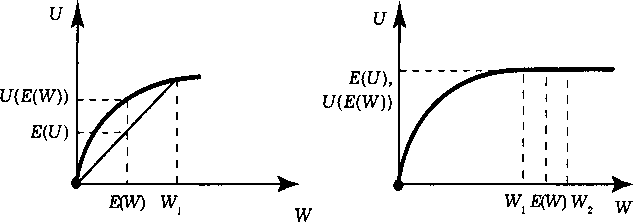
1) 2)

Рис. 12.1. Функции полезности, математического ожидания выигрыша и полезности математического ожидания в задании 699

1. Найдем математическое ожидание выигрыша (см. рис 12.1,1): E(W) = 0,5-100 + 0,5 =» 0 = 50, полезность математического ожи­дания согласно функции полезности: U(E(W)) = y]E(W) —

= 750= 7,1.

Полезность от обладания 100 руб. следующая: UiWJ =

= л/loo = 10, а в противном случае нулевая. Таким образом, ма­тематическое ожидание полезности: E(U) = 0,5-10 + 0,5-0 = 5.

2. Проделаем все операции согласно первому пункту (см. рис. 12.1, 2):

E(W)= 0,5-1 000 000 + 0,5-1 020 100 = 1 010 050;

U(E(W)) = yfE(W) = 71ОЮ 050 = 1005;

E(U) = 0,5-1000 + 0,5 1010 = 1005.

Вывод: индивид не расположен к риску.

686. Найдем математическое ожидание выигрыша: E(W) = = 0,2-5 + 0,8-10 = 9.

Полезность математического ожидания выигрыша соста­вит: U(E(W)) = (E(W))² =81. Ожидаемая полезность: E(U) = = 0,2-25 + 0,8-100 = 85. Если индивид будет гарантированно обладать суммой, которая принесет ему полезность, равную ожидаемой полезности от участия в данной игре, то ему бу-

дет безразлично участие в данной игре, ==> Е(х) = х² = 85, => => х = 9,2.

686. В случае благоприятного исхода фермер будет обладать суммой, обеспечивающей ему полезность, U = ^100 - 0,09д; в

противном случае: U = j80 + 0,91д,

E(U) = 0,ly/80 + 0,91q + 0,9 JlOO - 0,09д —> max.

0,1 0,5 0,91 0,9 0,5 0,09 _Л

—======== ===== = о, ==> о = 43.

л/80 -f 0,91д ->/100 - 0,09д *

686. В случае благоприятного исхода потребитель будет обладать суммой, обеспечивающей ему полезность, I/ = (10 - рд)², в противном случае: [7 = (д — рд)²,

£([/) = 0,5 (д - рд)² + 0,5(10-рд)²—j—>max.

0. 5 (д² - 2рд² 4- (рд)² 4- 100 - 20рд + (рд)²) = 0,5(100 + д² +

+ 2(рд)² ~ 20рд - 2рд²) = 50 + д² + (рд)² - Юрд ~ рд², (E(U)Y_q= 2д + 2др² ~ Юр ~ 2рд = 0; если д = 5, то р = 0,3.

686. Имея шанс заплатить “справедливую” премию, ней­тральный к риску потребитель предпочтет застраховаться пол­ностью. При цене страховки 5% это сумма 500 долл.

Ежегодно кооператив теряет 20 000 долл., что составляет 200 долл. на каждого члена кооператива. Организуя фонд под­держки от несчастных случаев с ежегодным взносом 200 долл., можно распределить риски между членами кооператива. В данной ситуации выгоднее содержать данный страховой фонд, чем пользоваться услугами страховой компании.