Решите задачи и ответьте на вопросы

556. Для любой точки на контрактной кривой должно вы­полнятся: MRS„ = MRS„.

с м

MRS_C = МЩ/МЩ = Y_c/X_c; MRS_M = MU™/MUy = YJX_M =

= (20 - Y_c)/(10 - X_c); так как У_г + Y_M = 20 и X_r + X = 10.

CM CM

Уравнение контрактной кривой: У_с/Х_с = (20 - Y_c)/(10 - Х_с)

и, следовательно, Y_c = 2Х_С.

556. Так как MRS_A = MRS_Bi то для любой точки на кон­трактной кривой

MRS_a = МЩ/МЩ = 2У_а/Х_а;

MRS_B = МЩ/МЩ = YJ 2Х_В, тогда TfJX_A = Y_B/2X_B = (60 - YJ/2(40 - Х_А).

Таким образом, 60Х_Л + 3X_AY_A - 160Y_A = 0.

556. На контрактной кривой должно выполняться: MRS_p = = MRS_n. Следовательно:

C_p/F_p = С_п/1 = (10 - С_р). Таким образом, уравнение кон­трактной кривой: С_р + C_pF_p - 10Fp = 0.

556. Утилитаристская функция общественного благососто­яния является суммой индивидуальных функций полезности:

п

W(u_v u_v ..., и_п) = где и. — функция полезности г'-го ин­

дивида; ^г=1

W — 2х + 5 + х² + у/х + х² + х + 1/2х = 2х² + 3,5х + л/х.

Следовательно, W = 2х² + 3,5а: + у[х.

556. 1. Функция общественного благосостояния, основыва­ясь на предположениях Д. Роулза, имеет следующий вид:

W(u_v и₂, ..., uj = min{u₁, и₂, ..., и_п}, где и. — функция полезно­сти г-го индивида.

На рисунке 11.11 представлены графики функции полез­ности, из которых видно, что в зависимости от обладания тем или иным количеством блага (х) функция общественного бла­госостояния имеет различный вид и соответственно значение. При обладании двумя и менее единицами блага (х) функция общественного благосостояния будет описываться функцией полезности Петрова П. П., а в остальных случаях функцией по­лезности Михайлова М. М.

Рис. 11.11. Определение функции общественного благосостояния в задании 658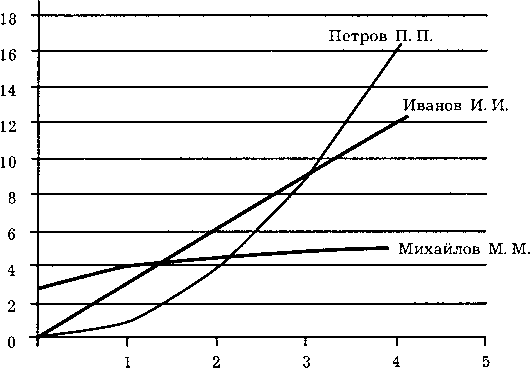

Yj^ai^Ui > ^min i^Um> ^Un> ^UJ•

i=1

Из задачи 658 известно, что в зависимости от количества благ функция общественного благосостояния описывается раз­ными зависимостями. Утилитаристская функция полезности известна из задачи 658 и постоянна. Необходимо решить два неравенства:

0,1х² + 1,5х + 0,4Vx + 1,2 > х² (для случая двух единиц блага (х) и меньше);

0,1а?² Н- 1,5л: + 0,4 л/х + 1,2 > у/х + 3 (от двух единиц блага (х) и больше).

Нетрудно рассчитать, что данные неравенства будут выполняться всегда. Следовательно, функция общественного благосостояния, рассчитанная по утилитаристскому принципу, больше по номинальному значению роулзианской функции полезности.

3. Эффективность производства

Верны ли следующие утверждения?

660. Да. Не выполняется условие Парето-эффективности.

661. Нет. В оптимальной точке выполняется равенство MRS = MRT.

662. Да. Так как оптимальные точки производства и потребления совпадают, то X* = Y* исходя из min{X,Y} (см. рис. 11.12).

663. Да. Оптимальные точки производства и потребления совпадают и лежат на кривой производственных возможностей (КПВ) в точке касания кривых безразличия Робинзона Крузо и КПВ.

664. Да. В оптимальной точке производства должно вы­полняться MRT^A = Р_Х/Р_Т В оптимальной точке потребления должно выполняться MRS^B = Р_х/Р_у. Если Робинзон производит обмен благами, то его уровень полезности при торговле выше, чем при отсутствии торговли. Это может выполняться только в случае, если точка потребления находится за пределами КПВ (см. рис. 11.13).

Выберите единственно правильный вариант ответа

660. г. Пусть С, F соответствующие количества собранных

орехов и пойманной рыбы, тогда уравнение КПВ: C/2 + F/l = 10.

A F

КПВ будет прямой линией. MRT = ⁼ 1/2.

660. а.

661. 

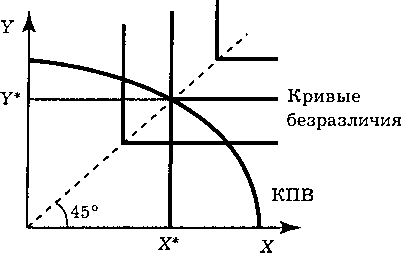
     Рис. 11.12. Определение оптимальной точки производства и потребления в задании 661

     

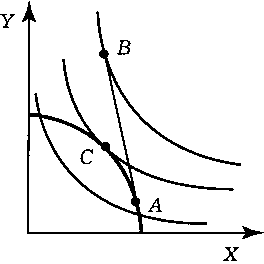
     Рис. 11.13. Определение оптимальных точек производства и потребления в случае торговли в задании 664

     г. В зависимости от вида изоквант Q^B контрактной кривой может быть любая из сторон диаграммы Эджуорта.

Решите задачи и ответьте па вопросы

660. 1. Все точки на контрактной кривой являются Парето- оптимальными. Таким образом, должно выполнятся: MRTS_y= = MRTS_X. Следовательно, K_x/L_x = K_y/L_y = (20 - К_х)/(10 - L_y), или К_х = 2L_x.

2. На кривой производственных возможностей распределе­ние ресурсов является Парето-оптимальным. Таким образом,

К_х = 2 L_x;

K_Y = 2 L_y. (1)

2L*;

к_х =

X

•К =

У

Y = L

(2)

Подставим (1) в производственные функции: X = L_v

•2L = 2L², или

У У ’

(Х/2)⁰'⁵ = L

(Y/2)⁰'⁵ = L .

Всего имеется 10 ед. труда, следовательно, L_x + L_y = 10. Подставим (2) и получим кривую производственных возможно­стей: (Х/2)⁰-⁵ + (Y/2)^0,5 = 10, или Х°’⁵+ У°-⁵= 10-2⁰’⁵.

660. Если Робинзон спит 12 ч в сутки, то на труд у него остается также 12 ч. Пусть L_c, L_F — соответствующее время, потраченное на сбор кокосов и ловлю рыбы, тогда L_c + L_F = 12.

Общее количество пойманной рыбы задается уравнени­ем: F = 2L_r Аналогично для кокосов: С = 3L_c В результате: С/3 + F/2 = 12, или 2С + 3F = 72.

660. задачи F = 4-L_F, С = 10L_r, где L_r,

     В данной задаче первоначально необходимо опреде­лить границу производственных возможностей. По условию

с’

время, потраченное

соответственно на ловлю рыбы и сбор орехов.

(1)

Уравнение кривой производственных возможностей: F/4 + С/10 = 6; 10F + 4-С = 240.

В оптимальной точке MRT = MRS.

^d(^10F + ^4С - 240)/dF _{л г}

MRT = — = 10/4 = 2,5.

d(10F + 4C-240)/dC ⁷

MR5 = MU_F/MU_C = C/F;

C/F = 2,5, или С = 2,5F.

Подставим в (1) и получим: 10F + 4-2,5F = 240. Следовательно, F = 12, С = 30.

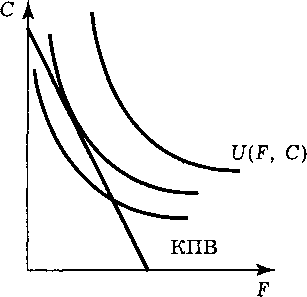
660. 1. Предельная норма трансформации:

d(F²+C²-l00)/dF 2 F F

IVllXl = — = — .

d(F² + С² - 100)/dC 2С С Если Робинзон ловит б рыб, то количество собранных орехов составит:

С = (100 - F²)^0,5 = 8, в результате MRT = 6/8 = 0,75.

2. Если Робинзон ловит 8 рыб, то количество кокосов со­ставит:

С = (100 - F²)^0,5 = б, в результате MRT = 8/6.

В оптимальной точке MRT = MRS.

Так как MRS = MU_F/MU_C = С/F, то

C/F = F/С или F = С. (1)

Подставим (1) в кривую производственных возможностей F² + С² = 100 и получим

С = F = V50 = 5л/2.

660. По условию задачи Х= 2Y. (1) Подставим (1) в кривую производственных возможностей: 2Y² + Y² = 80. В результате Y = 4, X = 8.

661. 1. Альтернативными затратами увеличения производ­ства сахара с 1 до 2 ед. будет снижение выпуска пшеницы на:

ДХ = (100 - I)⁰-⁵ - (100 - 4)^0,5 = 0,15.

2. АХ = (100 - 4²)^0,5 - (100 - 5²)^0,5 = 0,5.

3. АХ = (100 - 7²)^0,5 - (100 - 8²)^0,5 = 1,14.

Данная задача количественно демонстрирует закон возраста­ющих альтернативных затрат.

660. По условию задачи выпуск каждого товара увеличи­вался на 3%, таким образом:

Х₉₁ = 1,ОЗХ₉₀; Х₉₂ = 1,03Х₉₁;

Y₉i = 1,03Y₉₀; Y₉₂ = 1,03Y₉₁.

После небольших преобразований получим:

|Х₉₂ = 1,032Х₉₀;

[Y₉₂ = 1,032Y₉₀. W

Подставим (1) в ‘выражение для кривой производственных возможностей:

Х₉₂/1,03² + Y₉₂/l,03² = 10, или Х₉₂ + Y₉₂ = 10,609.

11. 2.4. Общее равновесие и экономика благосостояния Верны ли следующие утверждения?

660. Да. Основная проблема оценки благосостояния — это невозможность сравнения полезности некоторого блага для

различных индивидов, так как предельная ценность одного и того же товара неодинакова для различных категорий людей, а система ценностей не разработана.

660. Да. Существование монополии искажает цены. В мо­нополизированном производстве недопроизводство товара, а в другой (конкурентной отрасли) перепроизводство, что приве­дет к снижению цен на выпускаемую продукцию.

661. Нет. Налоги искажают общее равновесие, так как способствуют отклонению цен от равновесных.

662. Нет. Речь идет об одном и том же критерии, пред­ложенном для оценки благосостояния разными людьми в раз­личное время¹.

Выберите единственно правильный вариант ответа

660. б. Т. Ситовски оценивает посредством критерия Кал­дора—Хикса переход из одного состояния в другое дважды. На первом шаге необходимо проверить улучшение благосо­стояния при переходе из одного состояния в другое, а на втором — проверить, что обратный переход благосостояние не улучшает. Если соблюдаются эти условия, то благососто­яние повышается.

661. г. Предложены различные варианты описания эконо­мического понятия эффективности по Парето.

662. а. Освобождающиеся в монополии ресурсы перетека­ют в конкурентные отрасли промышленности. Это приводит к перепроизводству товаров в данных областях и снижению на них цен.

Решите задачи и ответьте на вопросы

660. Нетрудно проверить (подставив в уравнение кривой потребительских возможностей), что в первоначальном состо­янии точка А лежит на кривой потребительских возможностей (1) и внутри области потребительских возможностей (2). Ана­логично проверяем конечное состояние.

Согласно критерию Калдора—Хикса, во втором состоянии переход из точки А в точку В повышает общественное благо­состояние за счет увеличения полезности индивида А.

Если мы воспользуемся критерием Т. Ситовски, то полу­чим положительный ответ.

660. Максимально полезный эффективный выпуск харак­теризуется точкой касания кривой производственных возмож-

Рис. 11.15. Определение изменения благосостояния потребителя

в задании 682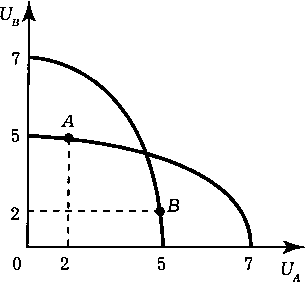

ностей и функции полезности. Для ее нахождения необходимо решить задачу максимизации функции полезности при задан­ном ограничении:

[7(М; П) -> шах, П² + М² = 50.

L = М П + (50 - П² - М²).

П - 2ХМ = 0 ГМ = П ГМ = 5

М - 2XU = 0 => 1 => <

П² + М² = 50 [ П² + М² = 50 [ П = 5

При данном виде кривых (см. рис. 11.16) и оптимальном товар­ном наборе соотношение цен будет 1:1.

660. Найдем эффективный выпуск в новых условиях.

П² + М² = 50 ГП = 6,32 П = 2М 1М = 3,16

Найдем оптимальный потребительский набор¹: 17(М; П) = М П.

S = p_uП + Р_мМ = 2Р_М-6,32 4- Р_м-3,16.

4Р_Л/Г

= 15,8/4 = 3,95.

Рис. 11.17. Определение эффективного выпуска в задании 684

П =

Эффективный выпуск и оптимальный набор товаров не со­впадают (см. рис. 11.17). Общество несет потери эффективности. Для достижения общего равновесия можно прибегнуть к нало­говой политике или субсидированию выпуска определенных то­варов, чтобы выровнять соотношение цен на пушки и масло 1 : 1.

3. Дискуссии, исследования и другие формы активной работы

685. Основные тезисы. Существует несколько критериев справедливости. Формулировка первого вопроса не соответ­ствует ни одному из них.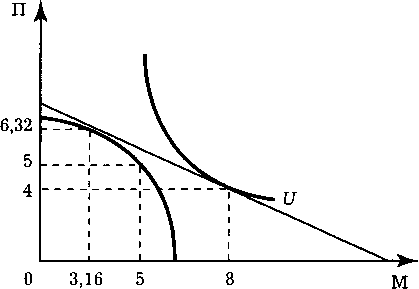

М=^|~= 15,8/2 = 7,9,

Но известны другие критерии. Так, в соответствии с кри­терием утилитаризма общество должно максимизировать сум­му индивидуальных полезностей. Для оптимального способа распределения благ Бергсон предложил максимизировать фун­кцию общественного благосостояния. Более полную информа­цию по этому вопросу можно найти в учебнике Р. М. Нурее­ва “Курс микроэкономики” на с. 362—369.