2. Уравнение линии бюджетного ограничения имеет вид:

^{м p}i ш ^pi

х, = -X,; => х, = 10 ^Lx,;

Р₂ Р₂ ^{1 2} Ю ¹

соотношение товаров в наборе 1:1=» решаем систему урав­нений:

100

Х_л =

10 + Р₂

=10 -х_л

² 10 ¹

Х₀ = Х_л

Последовательно изменяя значение цены на первое бла­го, построим кривую “цена—потребление”.

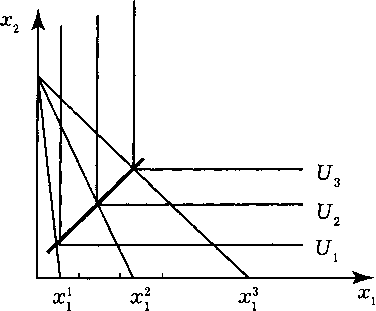
301. Согласно правилу долей найдем первоначальный на­бор Семенова С. С.:

1М 1 100 ₀ . 3 М 3100

х_с = = 2,5 л.; х = = 15 кг, так как потре-

0. 4Р_с 4 10 4Р_х 4 5

битель остается на прежней кривой безразличия, следователь­но: = (х*)^1/4 (х*)^3/4. Используя правило долей, запишем и решим систему уравнений:

. 1 М

^-44

. 3 м

х. =

^х 4 р;

х; = 1,25 х; = 18,89

<=11^ = 1,25

^с 4 20 • - ^{3 100} _ ^ ^Х* ~ 4 Р* ~ Р*

/ \^I 75

xfxf = (х;)^1/4 (х;)^3/4 => д/2,5 • 15³ = 4 1,25 •

Р

V^х х у

Р_х* = 3,97 => ДР_Х - Р_х* = 1,03 руб. На данную сумму необхо­димо снизить первоначальную цену хлеба, чтобы потребитель остался на прежнем уровне полезности.

301. Для функции полезности вида U(х,; х₂) = х*х\ опти­мальный набор в исходном состоянии согласно правилу долей следующий:

а М а М

х, = —, х₀ —.

¹ а + рР/ а + Р Р₂

Необходимо определить товарный набор, обеспечивающий прежний уровень полезности при новом соотношении цен:

а

М

Хп —

а + Р Р1* Р М

/ \а /

а М^л '

а + р Р,

р М а + р Р₂

2 /

\^а / а M'^w

а + Р Р*

. ^Г 1

р М а + р Р₂

2 /

В результате упрощения выражения получим следующее соотно-

0. 1

шение:

J “ о^-, если: 2Р, = Р'

P“Pf 2 (Pj)“ Р₂’^р ’

p“pf р;“р;^{р 1 1}

=>р-*-£

=> п ₂„ •

301. Опираясь на правило долей, найдем первоначальный набор Иванова И. И.:

1М 1 200 _1Л 1М 1 200 _с

x_v = = = 10 кг; = = = 5 кг, так как

^к 2Р_К 2 10 ^м 2Р_М 2 20

потребитель остается на прежней кривой безразличия, следо­вательно: ofxf = (а?к)^1/2 (^хм)^1/2, Используя правило долей, за­пишем и решим систему уравнений:

X*	_ 1 М*
к	“ 2 20
х'	_ 1 М*
м	” 2 20
50	М*2
	1600

, 1 М•

х_к =

к _{2 р}.

. 1 ЛГ

х_м =

2 Р.

х; = 1,25 х* = 15,003 М = 282,84

=> ДМ = М - М = 82,84 руб.

На такую сумму необходимо увеличить располагаемый доход потребителя, чтобы потребитель остался на прежнем уровне полезности.

3. Взаимодополняемость и взаимозаменяемость товаров и услуг

Верны ли следующие утверждения?

301. Да.

302. Нет. Выбор потребителя в этом случае является вы­нужденным и не зависит от цен на блага. В этом случае пре­дельная норма замещения равна нулю.

303. Да. Если угол наклона бюджетного ограничения совпа­дает с углом наклона кривой безразличия.

304. Нет. Например, лыжа и лыжный ботинок, а третий товар — валенок.

Выберите единственно правильный вариант ответа

301. б. Совместное использование взаимодополняемых благ значительно повышает их потребительские характеристики.

302. в. Чем меньше эластичность, тем больше взаимодо­полняемость. Свойство комплементарных благ.

303. в. Не существует жесткой зависимости при использо­вании данных товаров.

304. б. Чем меньше эластичность, тем больше взаимодо­полняемость.

305. г. Предельная норма замещения и у взаимозаменяе­мых товаров постоянна и равна положительному числу.

Решите задачи и ответьте на вопросы

301. 1. Рассчитаем первоначальную величину спроса на хлеб:

. М ^ 500

D = 50 Н = 50н = 54; спрос после изменения

Сборник —задач— 1

по микро­экономике 1

Сборник задач по микроэкономике 2

«.£.ae _{= A}.₈.^,_L,-,_; 301

эффект от изменения цены равен: AD_x = 70 - 54 = 16 кг в месяц.

Рассчитаем эффект замещения: найдем доход, который по­зволяет при цене молока в 1 рубль за литр потреблять его в пре­жних количествах: М² = М + AM = М + D*_x (Р_х - Р²) = 500 -

• 54(5 - 1) = 284; спрос на хлеб при данном уровне дохода и но-

М² 284

вой цене равен: D³_X = 50 + - = 50 + ■■■■ =61,36 кг. Эффект

25Р_Х 25 • 1

замещения: AD^S_X = D³_x - D^l_x = 61,36 - 54 = 7,36 кг; => эффект дохо­да: AD^d_x = ADI - AD^S_X = 16 - 7,36 = 8,64 кг.

Сборник —задач— 1

по микро­экономике 1

Сборник задач по микроэкономике 2

«.£.ae _{= A}.₈.^,_L,-,_; 301

эффект от изменения цены равен: A54 - 52 = 2 кг в месяц (на 2 кг сократится спрос на хлеб).

Рассчитаем эффект замещения: найдем доход, который позво­ляет при цене молока в 10 рублей за литр потреблять его в пре­жних количествах: М² = М + AM = М + D¹_x{P¹x - Р²х) = 500 -

• 54(5 - 10) = 770. Спрос на хлеб при данном уровне дохода и но-

М² 770

вой цене равен: DI = 50 + г = 50 + = 53,08 кг. Эффект

^х 25Р_Х 25-10

замещения: AD_x = D_x - D^l_x = 54 - 53,08 = 0,92 кг; =ф эффект до­хода: AD_X = AD_x^p - AD_X = 2 - 0,92 = 1,08 кг.

301. 1. Решим задачу на нахождение максимального значе­ния функции полезности при заданном бюджетном ограничении:

L = xf + х_с + ЦМ - Р_сх_с - Р_тх_т) -> max

хх_с

— = М - Р_сх_с - Р_тх_т = 0

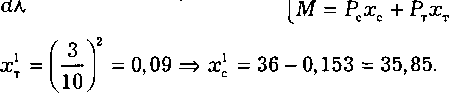
Рис. 4.12. Определение общего эффекта от изменения цены

в задании 314, 2

х²={—1 = 0,36 => х² = 36-0,36 = 35,64 =>ДхР=х²-х¹ =

I 1 ^с С С С

= 0,36 - 0,09 = 0,27.

2. Найдем первоначальный набор:

U(x_T, x_c) = min{3x_T; х_с}

'Зх_т = х_с , м Р

х_т = — - х_с => xj = 38,58; х²_с = 23,47 => Ах£ = х² - х* =

. ^Рт ^Рт

= 38,58 -23,47 = 15,11.

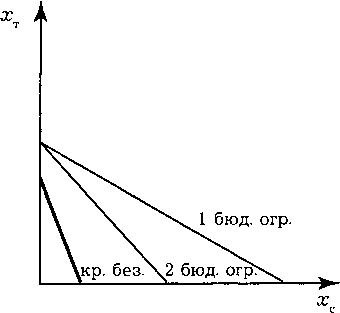
2. Решаем задачу линейного программирования. Уравнение бюджетного ограничения для первоначально­го состояния: х = 36 - 0,6х .

Сборник —задач— 1

по микро­экономике 1

Сборник задач по микроэкономике 2

«.£.ae _{= A}.₈.^,_L,-,_; 301

В первоначальном состоянии весь совокупный доход тра­тится на приобретение сметаны (см. наклон кривой безразли­чия и бюджетного ограничения на рис. 4.13).

х\ = 60; х²_с = 30 => Ах_с^р = х²_с - х\ = 60 - 30 = 30.

301. Исходный потребительский набор и набор после из­менения цен:

0. 1 М 1 1000

   М 3 1000

х: = = = 6,25; х* =

^fc 4P_fc 4 40 ⁿ 4P_n 4 10

1. M

= 75;

-^fc=T—= ⁵; = x²_k~x¹_k = 6,25-5 = 1,25.

⁴ Me

Найдем уровень дохода, который позволяет при новом соотношение цен достичь прежнего уровня полезности. Ис­пользуя соотношение из задачи 302, получим:

N°

\^а

р М а + р Р₂

а М а + Р Р;

а М а + р Р,‘

2 /

Р М а + р Р₂

2 У

\Р

1060

200

М = 1060 ==> х? =

= 5,3; =» эффект замены —

Ах^ь_к - х‘1 - х¹_к = 6,25 -5,3 = 0,95; эффект дохода — Ах^г_к = х²_к - х³_к = 0,3.

301. Применим правило долей и найдем исходный потре­бительский набор и набор после изменения цен:

3. М 3 500

4. Р “ 4 20

1 М 1 500

= 12,5; -х‘ =

' ^J п

= 18,75;

4Р_Ь 4 10

, 1 М 1 500 _{пс 2} 3 М 3 500

-х\ = = = 25; -х² = = = 18,75; =>

^к 4Р_к 4 5 ^п 4Р_П 4 20

=> Дх£ = xl -х¹_к = 25-12,5 = 12,5.

Найдем уровень дохода, который позволяет при новом соотношении цен достичь прежнего уровня полезности. Решаем систему уравнений:

=> эффект замены — Ax^s_k = х* - х\ = 21 -12,5 = 8,5; эффект дохода — Ах[ -х\-х\ = 25 - 21 = 4.

301. При соотношении цен на блага х_х и х₂ как 1 : 1 функ­ция полезности и линия бюджетного ограничения будут иметь одинаковый наклон. При дальнейшем снижении цены на пер­вое благо индивид перейдет на кривую безразличия более вы­сокого порядка. Следовательно, при снижении цены первого блага от текущего состояния до уровня цены второго блага уровень полезности индивида останется неизменным (рис. 4.14).

Рис. 4.14. Эффект изменения цены на первое благо в задаче 317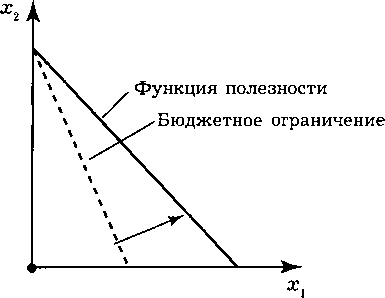

301. Первоначальный потребительский набор:

! 2М 2180 ! 1М 180

х_К = _г = = 40; х_х = = = 10.

^к зр; 3 3 ЗР_Х 18

„ , 2М J 1М 1180 _1С

После изменения цен: х_к = = 40; x_v = = = 15;

ЗР_К ^х ЗР_Х 3 4

Ах! =15-10 = 5.

Найдем уровень дохода, который позволяет при новом соотношении цен достичь прежнего уровня полезности. Далее получим:

'М'⁴' р V¹ X у

М* Р* ,

V X у

М

=> М* = 157 => х³_х = =— = 13

^х з р; 12

=> эффект замены — Дх* =х*-х* =13-10 = 3; эффект дохода — Дх^ = х\-х\ =15-13 = 2.

2. Дискуссии, исследования и другие формы активной работы

301. Основной тезис. Модель экономического человека (по­требителя) — условность, набор идеальных свойств, которые не встречаются в реальной жизни, так же как нельзя встре­тить в реальном мире идеальную прямую линию. Но такая модель необходима для построения теории потребительского выбора и прогнозирования рыночного поведения людей. Про­гнозы, получаемые с помощью данной модели, оказываются достоверными, это и служит критерием ее правдоподобности.