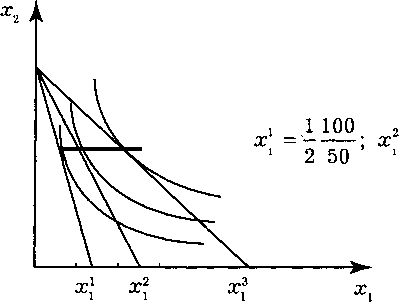- •Сборник задач по микроэкономике к “Курсу микроэкономики”
- •Содержание
- •Глава 9. Рынок труда
- •Глава 4. Поведение потребителя в рыночной экономике
- •Глава 9, Рынок труда
- •Некоторые методические рекомендации
- •Основные понятия
- •Вопросы и задачи
- •Метод экономической теории
- •Основные понятия
- •Вопросы и задачи
- •Сепусертпова этика
- •Хижина дяди Крома
- •Проклятие золотого креста
- •Хосе и Кармен
- •Четыре четверти жизни
- •Основные понятия
- •3.2. Вопросы и задачи
- •Рынок и трансакционные затраты
- •Увеличение предложения и спроса приведет к:
- •3.2.4. Эластичность спроса и предложения
- •Дискуссии, исследования и другие формы активной работы
- •Глава 4. Поведение потребителя в рыночной экономике
- •Основные понятия
- •Вопросы и задачи
- •Полезность и потребительский выбор
- •Наборы благ, имеющие одинаковую полезность:
- •Решите задачи и ответьте па вопросы
- •Вопросы и задачи
- •Общие вопросы.
- •Выбор производственной технологии.
- •Дискуссии, исследования и другие формы активной работы
- •Глава 6. Фирма как совершенный конкурент
- •Основные понятия
- •Вопросы и задачи
- •Верпы ли следующие утверждения?
- •Фирма: условия равновесия
- •Глава 7. Типы рыночных структур: конкуренция и монополия
- •Основные понятия
- •Вопросы и задачи
- •Совершенная конкуренция
- •7.2.2. Монополия и монополистическая конкуренция Верны ли следующие утверждения?
- •Дискуссии, исследования и другие формы активной работы
- •Глава 8. Типы рыночных структур: олигополия и монополистическая конкуренция
- •Основные понятия
- •Вопросы и задачи
- •Олигополия
- •Основные понятия
- •Вопросы и задачи
- •Спрос и предложение труда
- •Начертите функцию спроса фирмы на труд;
- •Определите, сколько работников будет нанято по ставке 4 долл./день.
- •Фирма-монопсония, продающая товары на совершенно конкурентном рынке готовой продукции, будет нанимать дополнительных рабочих на рынке труда до тех пор, пока не будет соблюдаться равенство:
- •Фирма-монополист на рынке готовой продукции будет нанимать дополнительных рабочих на конкурентном рынке труда до тех пор, пока не будет соблюдаться равенство:
- •Фирма, обладающая монопольной властью на рынке продукции, но являющаяся конкурентной на рынке факторов производства, будет:
- •Если на рынке труда определенной квалификации существует монопсония, то:
- •Фирма не обладает монопольной властью на рынке готовой продукции, но является монопсонией на рынке труда. По сравнению с аналогичными фирмами, но конкурентными на рынке труда она будет:
- •На сколько значения ставки зарплаты и объема занятости отличаются от значений при совершенной конкуренции на рынке труда.
- •Распределение доходов. Инвестиции в человеческий капитал
- •Вопросы по результатам исследования
- •Основные понятия
- •Цена, уплачиваемая собственнику капитала за использование его заемных средств в течение определенного периода; прирост, возвращаемый собственнику капитала.
- •Вопросы и задачи
- •Рынок земли. Экономическая рента
- •А) увеличит сельскохозяйственный спрос на землю;
- •Г) уменьшит сельскохозяйственный спрос на землю.
- •В) ответ на этот вопрос неоднозначен: и да, и нет;
- •Основные понятия
- •Вопросы и задачи
- •Анализ общего равновесия
- •Эффективность обмена
- •На рис. 11.1 показана диаграмма Эджуорта. Контрактной кривой будет:
- •Решите задачи и ответьте на вопросы
- •В табл. 11.1 представлены предпочтения индивидов от обладания некоторым видом благ (х).
- •В табл. 11.2 представлены предпочтения индивидов от обладания некоторыми видами благ.
- •Пользуясь роулзианским подходом;
- •Пользуясь утилитарным подходом.
- •Используя данные табл. 11.2, определите, в каких случаях утилитаристская функция общественного благосостояния больше роулзианской функции общественного благосостояния.
- •В экономике, производящей два блага, распределение ресурсов не является Парето-оптимальным, если можно увеличить производство обоих благ.
- •В задании 666
- •В задании 667
- •Множество точек в коробке Эджуорта, которые являются Парето-оптимальными;
- •Кривую производственных возможностей.
- •Робинзон Крузо живет на необитаемом острове и питается только рыбой и кокосами. Он может поймать 2 рыбы или собрать 3 ореха за 1 ч.
- •Предельную норму трансформации кокосов на рыбу (mrt), если он ловит б рыб; ловит 8 рыб;
- •Эффективное по Парето распределение — это распределение, при котором:
- •Потери эффективности, связанные с монополией, выражаются в том, что:
- •Решите задачи и ответьте па вопросы
- •Дискуссии, исследования и другие формы активной работы
- •Вопросы для дискуссии:
- •Основные понятия
- •Вопросы и задачи
- •Выбор в условиях неопределенности
- •В табл. 12.2 представлены данные двух проектов.
- •С вероятностью 50% он может выиграть 100 руб. Или ничего нё получить;
- •С вероятностью 50% он может выиграть 1 ооо ооо руб. Или 1 020 100 руб.
- •Спекуляция и ее роль в экономике
- •Риск инвестиционных решений
- •Решите задачи и ответьте на вопросы
- •Основные понятия
- •Вопросы и задачи
- •Внешние эффекты
- •Решите задачи и ответьте на вопросы
- •Потлач на весь мир
- •Общественные блага.
- •Дискуссии, исследования и другие формы активной работы
- •Основные понятия
- •Вопросы и задачи
- •Предпосылки анализа
- •Методологический индивидуализм подразумевает:
- •Дискуссии, исследования и другие формы активной работы
- •Вопросы и задачи
- •Развитие предмета экономической теории
- •Ответьте на вопросы
- •Метод экономической теории
- •Вопросы и задачи
- •Хижина дяди Крома
- •Хосе и Кармен
- •Четыре четверти жизни
- •Основной тезис.
- •3.2. Вопросы и задачи
- •Рынок и трансакционные затраты
- •Спрос и предложение
- •Пример исследования.
- •Вопросы и задачи
- •Полезность и потребительский выбор
- •2. Уравнение линии бюджетного ограничения имеет вид:
- •Вопросы и задачи
- •Общие вопросы.
- •Глава 6. Фирма как совершенный конкурент
- •Вопросы и задачи
- •Глава 7. Типы рыночных структур: конкуренция и монополия
- •Вопросы и задачи
- •Совершенная конкуренция
- •Дискуссии, исследования и другие формы активной работы
- •Глава 8. Типы рыночных структур: олигополия и монополистическая конкуренция
- •Вопросы и задачи
- •Олигополия
- •Картеля 7 7 своб конкур 7
- •Исследование рынка (отрасли).
- •Вопросы и задачи
- •CnpoG и предложение труда
- •Верны ли следующие утверждения?
- •Вопросы и задачи
- •Рынок капитала. Ссудный процент
- •Рынок земли. Экономическая рента
- •Дискуссии, исследования и другие формы активной работы
- •Глава 11. Общее равновесие и экономическая эффективность
- •Вопросы и задачи
- •Решите задачи и ответьте на вопросы
- •Эффективность производства
- •Вопросы и задачи
- •Рынки с асимметричной информацией
- •Выберите единственно правильный вариант ответа
- •Решите задачи и ответьте на вопросы
- •Спекуляция и ее роль в экономике
- •Вопросы и задачи
- •Потлач па весь мир
- •Общественные блага.
- •Г. По определению чистых общественных благ.
- •Дискуссии, исследования и другие формы активной работы
- •Вопросы и задачи
- •Предпосылки анализа
- •Дискуссии, исследования и другие формы активной работы
- •Сборник задач по микроэкономике
- •127214, Москва, Дмитровское ш., 107
- •170024, Г. Тверь, пр-т Ленина, 5. Телефон: (0822) 44-42-15 Интернет/Ноте page - www.Tverpk.Ru Электронная почта (e-mail) -sales@tverpkru
Вопросы и задачи
Полезность и потребительский выбор
Верны ли следующие утверждения?
Да. Как правило, предельная полезность каждой дополнительной единицы блага неуклонно уменьшается. Однако бывают исключения. Это зависит от функций полезности (рис. 4.5, 3).
Нет. Максимум удовлетворения общей полезности, когда предельная полезность становится равной нулю.
Нет. Цена блага определяется его предельной полезностью. Если дальнейшее потребление приносит вред (предельная полезность блага отрицательна), то общая полезность снижается.
Нет. В равновесии предельные полезности денежных единиц при разных вариантах использования равны.
Да. Согласно теории рационального выбора.
Да. Так как зависит от свойства товара.
Нет. Эффект присоединения к большинству — эффект увеличения потребительского спроса, связанный с тем, что потребитель, следуя общепринятым нормам, покупает тот же товар, который покупают другие. Данный фактор непосредственно не связан с присущими экономическому благу факторами.
Выберите единственно правильный вариант ответа
а. Предельная полезность с каждой дополнительной единицей блага неуклонно уменьшается. Максимум достигается, когда предельная полезность равна нулю.
б. Неравенство взвешенных по ценам благ свидетельствует о нерациональном распределении благ в наборе, что делает одни блага предпочтительнее других, в результате происходит выравнивание данных отношений.
а. Исходя из первого закона Госсена.
в. Престижное или демонстративное потребление, когда товар используется не по прямому предназначению, а для того, чтобы произвести неизгладимое впечатление.
в. Ординалистская теория полезности строится на некоторых гипотезах о способах ранжирования наборов благ, но в ней отсутствует предположение о возможности количественного измерения степени удовлетворенности от потребления определенного количества благ.
б. Потому, что полезность является не объективной ценностью блага, но субъективным отношением индивида к данному благу.
г. Верно как а, так и б.
2. См. известный парадокс воды и алмазов.
а. В основе принятия решения лежит сравнение предельной полезности и стоимости.
Решите задачи и ответьте на вопросы
Максимум удовлетворения полезности будет находиться в точке, где предельная полезность равна нулю, т. е. выпол-
/Л/Тг Т\
няется
условие MU
=
^
= 0. Следовательно:
U'(Q) = -4Q = 0, => Q = 0;
U'(Q) = 1 - 2Q = 0, => Q = 1/2;
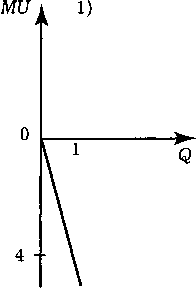 U'(Q)
=
2Q
-
3Q2
=
0, => Q
=
0; Q
=
2/3.
U'(Q)
=
2Q
-
3Q2
=
0, => Q
=
0; Q
=
2/3.
Рис.
4.5.
Виды кривых предельных полезностей в
задаче 264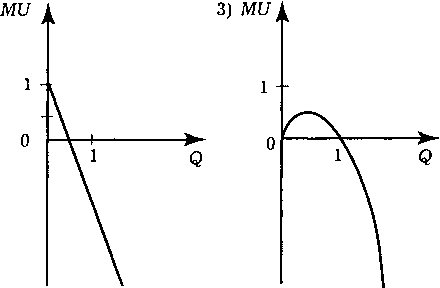
Предельная полезность данного блага равна частной производной общей полезности: MU = -^-.Следовательно:
MUX=^ = 2; MUy=^- = l;
дх у ду
MUx=^ = 4x; MUv=j- = 1;
MU = — = р^-‘у1’15 = pf—^
Эх \х
У.
В положении равновесия взвешенные предельные полезности будут равны. Выполняется условие:
MUA MUB миБ
^ = - = ^ => а = 20.
РА Рв Рв
В положении равновесия взвешенные предельные полезности будут равны. Выполняется условие:
миА мив мив с q о
^ = = ^-,=> а = 56, В = 2.
Р Р Р
А Б
Как и в предыдущих задачах,
MU±=MUJL = MlL а=15 ^ар = 75. РА Рв РБ ’ 5 Р’ Н
При выполнении данного соотношения потребитель будет находиться в положении равновесия.
Предельная полезность равна частной производной полезности данного блага:
ми = — => миа = 6; MUb = 8; MU = 4.
dQ “ 6 с
„ MUa MUC _ „
Согласно соотношению а. = £- => Р = 2.

Э
U
_тт
Э U![]()
![]()
М7в = 1,М7ь=1;Рв=0,2.
Мир потребительских предпочтений: закономерности развития
Верны ли следующие утверждения?
Нет. Множественность видов потребления. Каждый потребитель желает потреблять множество разнообразных индивидуальных благ.
Да. В положении равновесия предельная полезность блага равна предельным затратам потребителя.
Нет. Кривая безразличия показывает различные комбинации двух экономических благ, имеющих одинаковую полезность для потребителя.
Да. В классической теории поведения потребителя рассматривается только отрицательный наклон кривых безразличия. На самом деле в случае если один из товаров — антиблаго, то кривая безразличия имеет положительный наклон.
Да. В случае положения равновесия потребителя (в окрестностях точки равновесия).
Да. Увеличение денежного дохода означает смещение бюджетной прямой вправо вверх. Аналогичный результат может быть получен при снижении цен обоих продуктов.
Нет. Изменяется цена только одного блага. Доход и цена второго блага фиксированы.
Нет. Кривая Энгеля показывает соотношение между денежным доходом и количеством покупаемого товара.
Выберите единственно правильный вариант ответа
г. Перечислены свойства кривой безразличия.
а. Рассматривается с геометрической точки зрения как наклон касательной к кривой безразличия.
г. Разные подходы, описывающие одну зависимость параметров.
а. Изменяется цена одного блага. Цена второго и располагаемый доход постоянны.
а. Одно из свойств функции полезности.
г. Потому, что в равновесии происходит касание кривой безразличия с бюджетным ограничением.
г. Геометрйческая интерпретация предельной нормы замещения.
в. По определению: бюджетная линия — это линия, показывающая, какое количество товара потребитель может приобрести на весь свой доход.
а. Потому, что относительные цены товаров остаются неизменными.
а. Потому, что предельная норма замещения является постоянной для товаров совершенных субститутов.
а. Все перечисленное верно для точки потребительского оптимума, но равновесия потребитель достигает потому, что у него нет возможности более оптимально распределить получаемый доход.
Решите задачи и ответьте на вопросы
Проиллюстрируем решение рис. 4.6.
Если набор А' предпочтительней набора В' значит полезность обладания набором А' выше, чем полезность от обладания набором В' Следовательно, набор А' должен принадлежать области “Северо-восточного угла”, выходящего из точки В'.
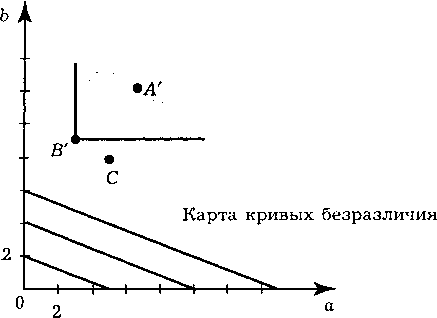
Проиллюстрируем решение рис. 4.7.
Набор А! принадлежит области “Северо-восточного угла” выходящего из точки В'. Параметр а не влияет на выбор набора А!. Кривые безразличия не пересекаются, существует аксиома ненасыщаемости.
Рис.
4.7.
Определение выбора потребителя в
задании 291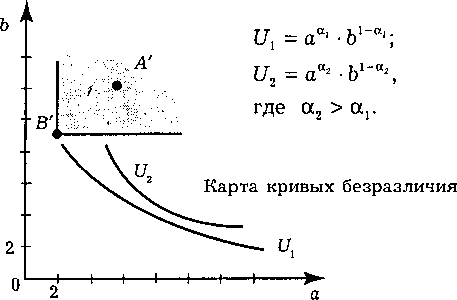
Решаем задачу на условный максимум функции: U(£l9 х2) = х“ х\ (при условии Рххх + Р2х2 = М).
L = х“х2ь + А, (М - Рххх - Р2х2) —> max
ах“
'х2
= ЯР,
bx“
х2
1
= ХР2
=>
PjXj
+
Р2х2
= ш
=
ах^х^-ХР,
=0 dxx
= ъх“х!-яр,
=о =>
7 VI L
dxx
dL
=
М - Рх, - Р2х2
- 0 dk
112
2
ах“
_ bx“
х£
1
а
М 1
" а + b
Р,
b
М
а
+ Ь Р9
Р2х2
=-Р,ж1
X,
=
Рг
Правило долей будет использоваться ниже для решения задач оптимизации, если функция полезности имеет вид функции Кобба—Дугласа.
ОАО т/г „ а М Ъ М
Используя правило долей: хл = ; х9 = ,
а + Ъ Рх а+ Ъ Р2
получаем:
1 240 _ 1 240
!) *каР = “■— = 60 кг; хдр = = 20 ед.;
2)
Жкар
=
Хдр = 7, ,
,,
-7“
=80
кг;~~:
• г/:
'V
= 13>3
еД-
. м
1, 2. В точке оптимума спрос на товары равен: хх = —-
. М , 1
м х2 = (см. правило долей) =>
2 Р2
в п. 1 и 2 ответы одинаковы:
М_= 240 М_ = 240
1 2хГ 2-6 2 2х* 2-8
„ , 1М . 3 м
В точке оптимума хх - ; х2 = ;
М_= 240 ^3м = 3^40 =
1 4х[ 4 ■ 6 2 4х; 4-8
т, - « м ь м
Используя правило долей: хл = ; х2 = - ,
получаем: а + Ь рг а + ЪР\
х1н = — — - 2М1 = Мг=> 2х1 = Х2Ы.
м 1/4 + 1/ 2 Рм 12 м м
Объемы потребления возрастут в два раза.
т/г „ а М Ъ М
Используя правило долей: хх = ; х2 = ,
а+ Ъ Р1 а+ Ъ Р2
получаем:
для начального состояния:
_ 1/2 М _ 1 М _ 1/2 М = 1 М
*кеф~1/2 + 1/2Ркеф ~2Ркеф’ Хкар “ 1 /2 + 1 /2 Ркар “ 2Ркар’
для конечного состояния:
1/3 М ' 1 м
^кеф
1 / 3 + 1 / 3 Ркеф 2 Ркеф
^кар
/ 3 +1 / 3 Ркар ~ 2 Ркеф ’ оптимальный набор не изменится;
для начального состояния:
_ 1/2 М _ 1 М _ 1/2 М _ 1 М
хкеф - 1/2 + 1/ 2 Ркеф ~~ 2 Ркеф ’ Хкар - 1/2 + 1/ 2 Ркар _ 2 Р^р
для конечного состояния:
1/2 М _ 2 М _ 1/4 М _ 1 М
1 / 2 + 1 / 4 Ркеф 3 Ркеф ^ 1 / 2 + 1 / 4 Ркар 3 Ркар
потребление кефира увеличится на 16,7%, потребление картофеля снизится на 16,7%.
Сборник —задач— 1
по микроэкономике 1
Сборник задач по микроэкономике 2
«.£.ae = A.8.^,L,-,; 301
функции полезности выполняется следующее соотношение:
хх _ 1 х2 2*
При соотношении цен 2 : 1 соотношение благ в оптималь-
х 1 ном наборе будет — =
х2 1
Решаем задачу на нахождение максимального значения функции полезности при заданном бюджетном ограничении:
L = х\ + х2 + X (М - Р^ - Р2х2) —> шах
М = 2Ргх\
Г
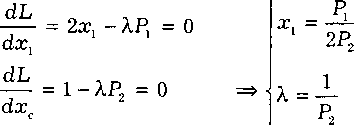
![]()
![]() М
= 2Р2х\
- Р2хг
м = Р2
(2х? - х2
М
= 2Р2х\
- Р2хг
м = Р2
(2х? - х2
Зная первоначальный набор, найдем стоимость единицы первого и второго блага:
Рх = 4,8; Р2= 0,12.
Затем найдем уровень располагаемого дохода:
М = р2(2х12 -х2) = 0,12(200 + 15) = 25,8.
1. Некомпенсированный спрос на первое и второе блага имеет следующий вид (согласно правилу долей):
Ъ М _ 1 М _ М _ЗМ_М а + Ь Р2 ^ Xl ~ 4 15 “ 60 ’ _ 4 30 “ 40 ’
![]()
бюджетное ограничение: М = Рххх + Р2х2 => М = 1Ъхх + 30х2, тангенс угла наклона бюджетного ограничения: — = i. Изменяя значение параметра М, строим кривую “доход—потребление” на основании полученных значений из следующих соотношений:
х, = —; х9 = —; М = 15х, + 30х9.
1 60 40
2. Как и в предыдущем случае, бюджетное ограничение имеет вид: М = 15хх + 30х2. Соотношение товаров в наборе 2 : 5. Необходимо решить систему уравнений:
ГМ = 1Ъхх + 30х2 [2хх = Ъх2.
Изменяя величину параметра М, находим из соотношений в системе уравнений оптимальные наборы и на этом основании строим кривую “доход—потребление”.
строим
кривую “цена—потребле-
2
Р j
2
Pj
ния”
по точкам, последовательно изменяя
цену на первое благо, например, Pj
=
50, Р2
= 20, Р^ = 10, (порядок выбора цены на первое
благо не имеет значения).
286 Ответы
и решения
Х2
|
\
Рис.
4.8. Кривая “доход—потребление” в
задании 299, 1
Рис.
4.9.
Кривая “доход—потребление” в задании
299, 2
300.
1. Согласно правилу долей функция
некомпенсированного спроса на товар
описывается следующей функцией:
1
М 1 100 1 М 1 100
2
10
постоянно.
На
2
Р1
2 ?!
1
М 1 100 основании: Xj
=
— — = —
х0
X,
—
х,
=
2
2 Р,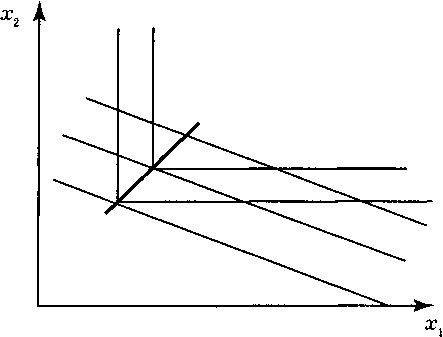
1
100 2
20
’
Рис.
4.10.
Кривая “цена—потребление” в задании
300, 1
з 1
100
Х'
~
2 10 '