1.6 Множення решіткою

Як було раніше згадано здавна люди прагнули навчитись швидко рахувати. Ось на приклад у середній Азії у давнину множили за допомогою решітки. Цей спосіб є дуже легкий але дієвий. Записуємо числа над і збоку решітки, перемножуємо цифри записуємо отримані значення у трикутники у верхній десятки у нижній одиниці. Перемноживши додаємо цифри по діагоналі. Відокремлюємо дві цифри комою і отримуємо відповідь.

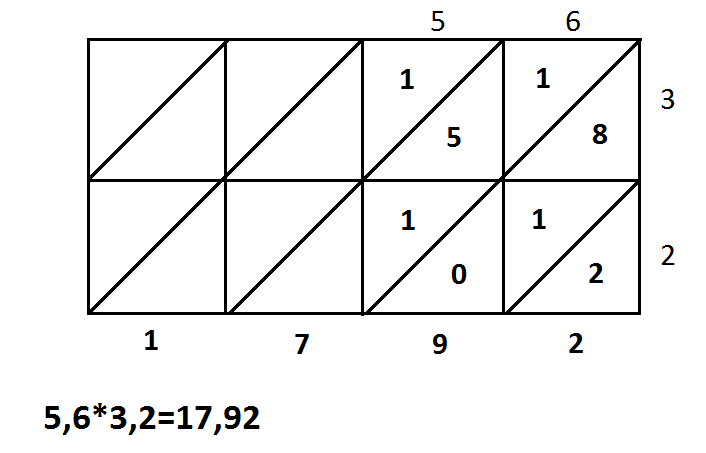
12

Розділ 2 Вивчивши степінь і арифметичний корінь квадратний я задав собі запитання.

Чи можна швидко і зручно піднести до квадрату число або ж добути з нього корінь ?

2.1 Піднесення до квадрату чисел, що закінчуються на 5

Дуже легкий і зручний спосіб піднесення до квадрату, коли число закінчується цифрою 5

Щоб піднести до квадрату число яке закінчується цифрою 5. (наприклад 85) множимо число десятків (8) на нього ж плюс одиниця (8∙9=72) і приписуємо 25 (7225).

25²; 2∙3=6; 625;

45²; 4∙5=20; 2025;

145²; 14∙15=210; 21025.

Цей спосіб випливає із формули (10х+5)²=100х²+100х+25=100(х+1)+25.

Таким же способом можна підносити до квадрату десяткові дроби, які закінчуються на цифру 5.

8,5²=72,25;

14,5²=210,25.

27. Так як 0,5= ,а 0,25=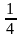 , то таким же способом можна підносити до квадрату ті числа , які закінчуються на дріб .

(8 )²=72 ;

(14 )²=210

При усному піднесенні до квадрату зручно користуватися формулою 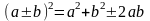. Наприклад:

41²=40²+1+2∙40=1601+80=1681;

69²=70²+1-2∙70=4901-140=4761;

36²=35²+1+2∙35=1296.

Цей спосіб більш зручний для чисел які закінчуються на 1, 4, 6,9.

13

2.2 Піднесення до квадрату цілого числа А, якщо відомий квадрат попередного(A-1) або наступного (A+1) числа.

З виразу (А + 1)² = А² + 2А + 1 отримуємо ряд зручних формул: (А + 1)² = А² + А + (А + 1) А²=(А + 1)² - 2  (А + 1) + 1, або А²=(А+1)²-(А + 1)- А

Вивівши зручні формули можна леко обчислювати квадрат якщо ми знаємо квадрат попереднього або наступного чила.

2.3 Обчислення по формулі (а+b)(a-b)=a²-b².

Нехай потрібно виконати усно множення 52∙48 подумки перетворюємо ці множники на (50+2)(50-2) і використовуємо приведену формулу (50+2)(50-2)=50²-2²=2496. Подібним чином виконують і в інших випадках. Коли один множник зручно представити в вигляді суми двох чисел, а другий в виді різниці тих же чисел. 69∙71=(70-1)(70+1)=4899

Вказаним прийомом зручно користуватися і для обчислення слідуючого виду:

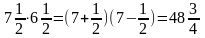
Корисно знати

37∙3=111. Заповнивши це, легко виконувати усно множення числа 37 на 6, 9, 12 і т.д.

37∙6=111∙2=222;

37∙9=111∙3=333.

7∙11∙13=1001. Заповнивши це, легко обчислюються усно множення слідуючого виду.

77∙13=1001; 91∙11=1001; 143∙7=1001;

77∙26=2002; 91∙22=2002; 143∙14=2002;

77∙39=3003; 91∙33=3003; 143∙21=3003 і.т.д.

14

Розділ 3

3.1 Множення на пальцях.

Для того, щоб помножити два числа необхідно як мінімум знати таблицю множення. Однак, в одному випадку можна обійтись і без неї. Це в тому разі, якщо необхідно помножити на 9.

Отже, два способи множити одноцифрові числа на 9 за допомогою пальців рук.

Спосіб І

Покладемо обидві руки перед собою на стіл і подумки пронумеруємо пальці зліва направо. Тепер піднімемо той палець, порядковий номер якого відповідає числу, яке множимо на 9. Залишилось тільки порахувати кількість пальців зліва і справа від піднятого. Зліва - кількість десятків, справа - кількість одиниць.

Наприклад, помножимо 9 на 7. Піднімаємо сьомий по порядку палець і отримуємо відповідь - зліва 6 пальців, справа 3, маємо 63.

Спосіб ІІ

Кладемо перед собою обидві руки і загинаємо таку кількість пальців, що відповідає числу, яке множимо на 9. Тоді кількість десятків у відповіді буде на 1 менше, ніж було загнуто пальців, а кількість одиниць - кількості пальців, що лишилися незагнутими.

Наприклад, щоб помножити 3 на 9, загинаємо 3 пальці і у відповіді маємо 3-1=2 (десятки) і (рахуємо незагнуті пальці) 7 одиниць. Разом 27.

15

Множення чисел від 6 до 10.

Отже, Вам необхідно перемножити два числа від 6 до 10. Операція множення проводиться за наступною схемою.

Подумки пронумеруйте пальці своїх рук наступним чином:

Спробуємо помножити 9 на 7. Для цього Вам треба загнути на першій руці палець з номером 9, а на другий відповідно 7.

Далі починаємо рахувати за наступним правилом: порахуйте скільки пальців у Вас всього до загнутих включно (в нашому випадку їх 6 — на першій руці під номерами 6,7,8,9 і на другій під номерами 6 і 7). Далі кількість цих пальців множимо на 10. У нашому випадку 6х10 = 60, тепер порахуйте кількість пальців, які залишились (пронумеровані червоним кольором) на кожній руці окремо, в нашому випадку на першій руці 1, на другій 3, перемножимо ці два числа: 1х3 = 3. У висновку складемо свої дві відповіді, тобто 60 і 3 : 60 +3 = 63, значить 9х7 = 63.

Тепер помножимо на 7 8:

Кількість пальців, пронумерованих блакитним кольором — 5, множимо 5 на 10, отримуємо 50, кількість пальців, пронумерованих червоним кольором, на першій руці 3, на другій — 2, перемножимо 2 і 3, отримуємо 6. Складаємо отримані відповіді 50 +6 = 56, значить 7х8 = 56.

Ось так виглядає операція множення чисел від 6 до 10.

16