Інтеграл та його застосування. Програма

Первісна. Невизначений інтеграл та його властивості. Основні табличні інтеграли. Основні властивості та обчислення визначеного інтеграла. Інтегрування заміною змінної (методом підстановки). Метод інтегрування за частинами. Визначений інтеграл та його геометричний зміст. Обчислення площ фігур за допомогою визначеного інтегралу. Застосування інтегралу до розв’язання фізичних задач.

Зміст уміння для даної спеціальності: Використовувати математичні методи при розрахунках економічної ефективності технологічних процесів виготовлення типових зварних конструкцій. Визначати тип зварної конструкції, призначення її основних елементів; виконувати розрахунки нескладних елементів зварних конструкцій на міцність та визначати розміри їх перерізів при статичному навантаженні. Розраховувати та вибирати параметри режиму зварювання тиском. Розраховувати та вибирати параметри режиму зварювання плавленням.

Методичні вказівки

1. Вивчити навчальний матеріал за підручником В. Т. Лисичкин, И. Л. Соловейчик "Математика" розділ V, чи за будь-яким іншим підручником з поданих у списку літератури.

2. Ознайомитися з методичними вказівками до даної теми та розібрати розв’язання прикладів з даного посібника.

3. Дати відповіді на питання та виконати вправи для самоперевірки. Поняття невизначеного інтеграла. Табличні інтеграли.

Якщо - первісна для на деякому проміжку, то функція , де , також є первісною для функції на цьому проміжку.

Причому, .

Сукупність всіх первісних функцій на інтервалі < < називають невизначеним інтегралом від функції на цьому інтервалі та пишуть .

Таблиця інтегрування:

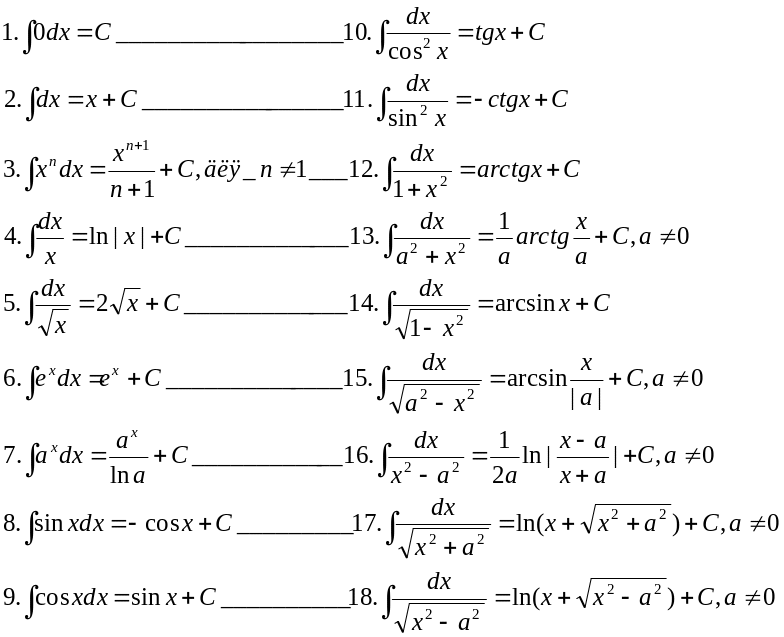
Приклад №1. Знайти інтеграл

Розв’язання:

Приклад №2. Знайти інтеграл

Розв’язання:

Приклад №3. Знайти інтеграл

Розв’язання:

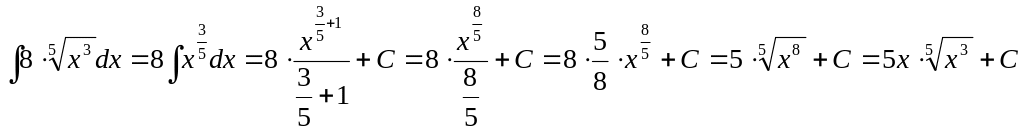Приклад №4. Знайти інтеграл

Розв’язання:

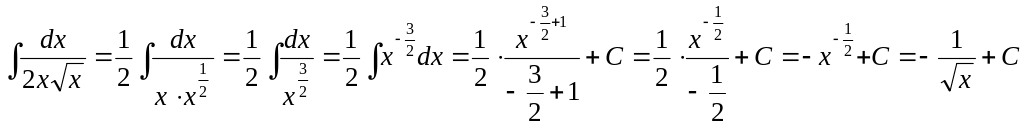
Основні властивості та обчислення визначеного інтеграла.

Якщо - первісна для функції , тоді приріст первісних функцій, при зміні аргументу від х = а до х = в, називається визначеним інтегралом та позначають , де а та в – відповідно нижня та верхня границі інтегрування, тобто = .

Для обчислення визначеного інтеграла використовують формулу Ньютона-Лейбніца:

З цієї формули легко побачити порядок обчислення визначеного інтеграла:

1) знайти невизначений інтеграл від даної функції;

2) в отриману первісну підставити замість аргументу спочатку верхню межу,

потім нижню межу інтегрування;

3) результат відняти.

Приклад №5. Обчислити інтеграли: а) ; б)

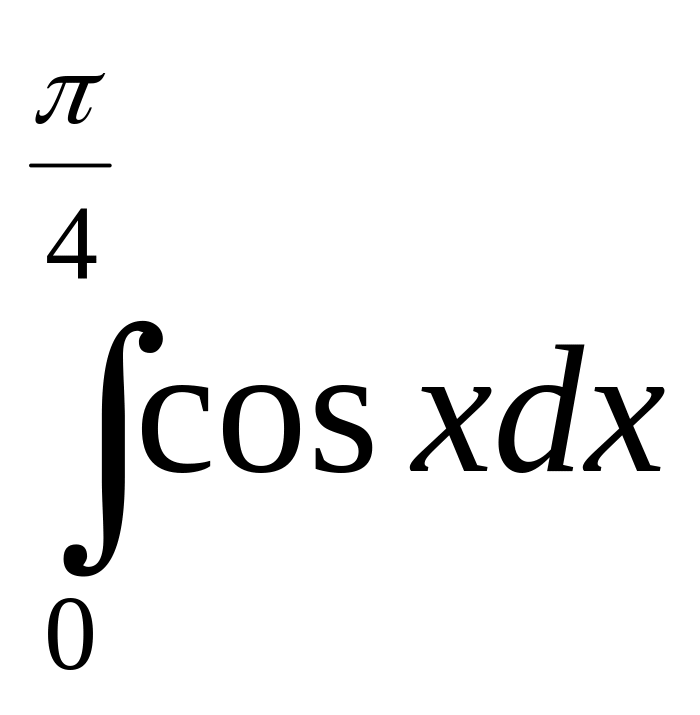
Розв’язання:

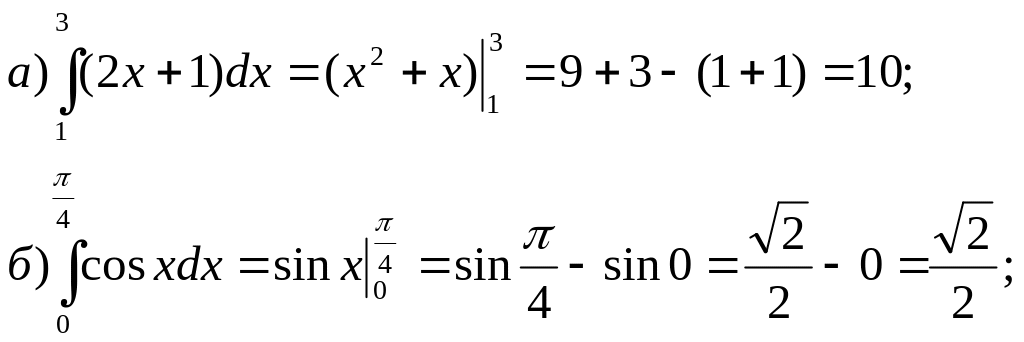
Властивості визначеного інтегралу

1. Визначений інтеграл з однаковими границями інтегрування дорівнює нулю:

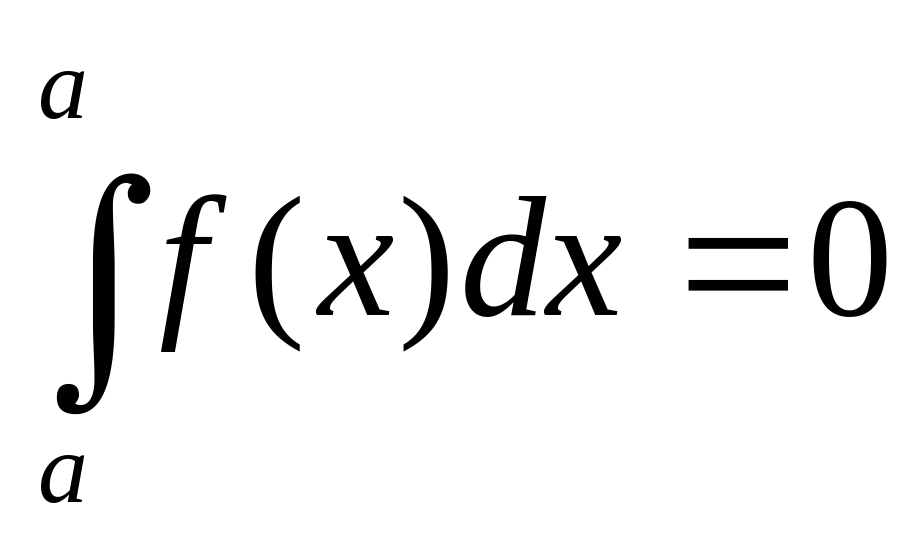
2. При перестановці границь інтегрування знак інтегралу змінюється на протилежний: .

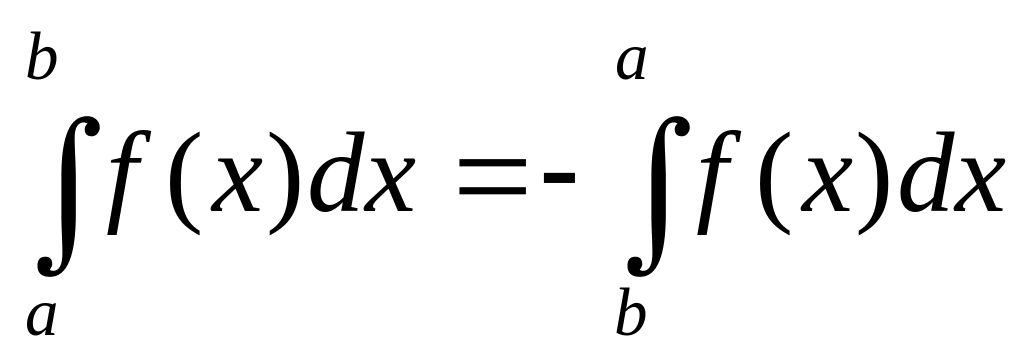3. Постійний множник можна виносити за знак інтегралу: .

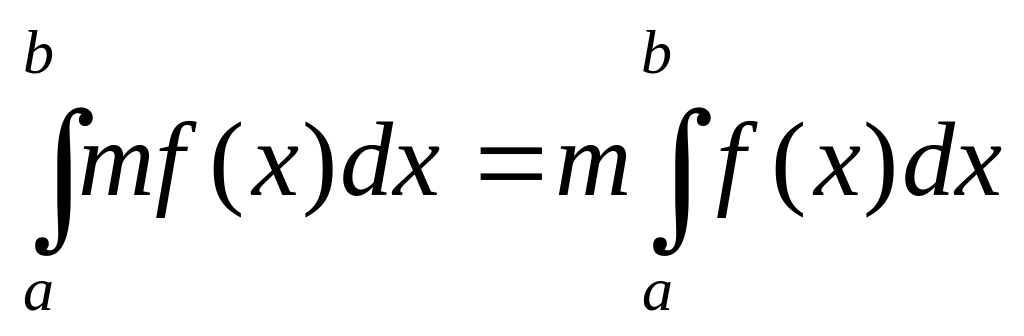4. Для довільного числа с визначений інтеграл в межах від а до в можна обчислити як суму двох інтегралів в межах від а до с та від с до в: .

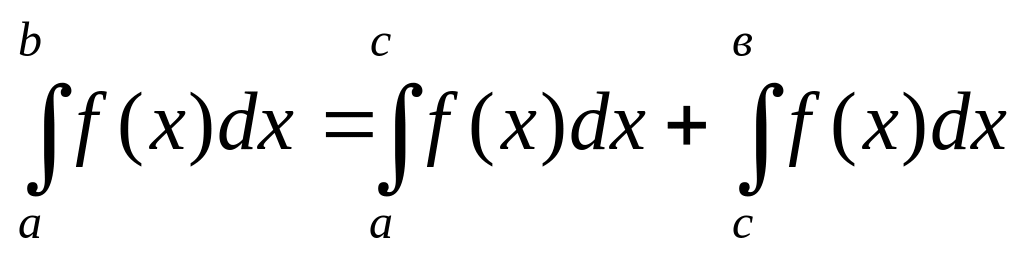5. Визначений інтеграл від алгебраїчної суми функцій дорівнює алгебраїчній сумі інтегралів цих функцій: .

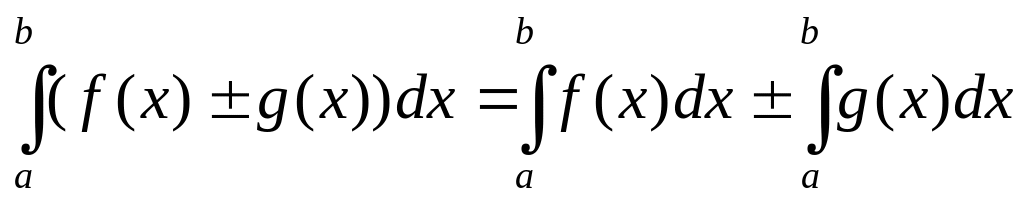Інтегрування методом підстановки (заміна змінної).

Зміст методу – введення нової змінної, після чого даний інтеграл перетворюється на один з табличних.

Схема методу для невизначеного інтегралу:

1) частину підінтегральної функції замінити новою змінною;

2) знайти диференціал від обох частин заміни;

3) весь підінтегральний вираз виразити через нову змінну;

4) знайти отриманий табличний інтеграл;

5) зробити обернену заміну.

Приклад №6. Знайти інтеграл

Розв’язання:

Приклад №7. Знайти інтеграл

Розв’язання:

Схема методу для визначеного інтегралу:

1. частину підінтегральної функції замінити новою змінною;

2. за допомогою заміни обчислити нові границі інтегрування;

3. знайти диференціал від обох частин заміни;

4. виконати заміну підінтегрального виразу та границь інтегрування;

5. знайти отриманий табличний інтеграл;

6. за формулою Ньютона-Лейбніца обчислити його.

Приклад №8. Обчислити

Розв’язання:

Приклад №9. Обчислити

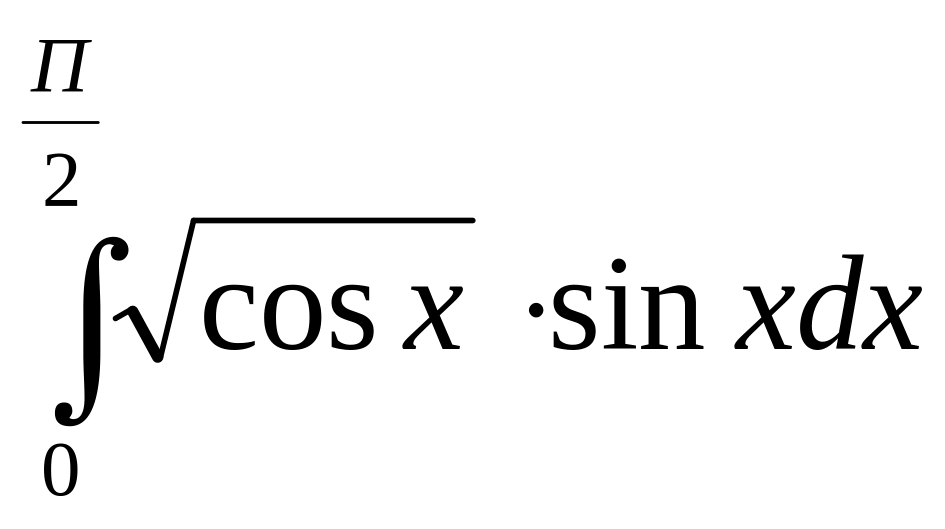
Розв’язання:
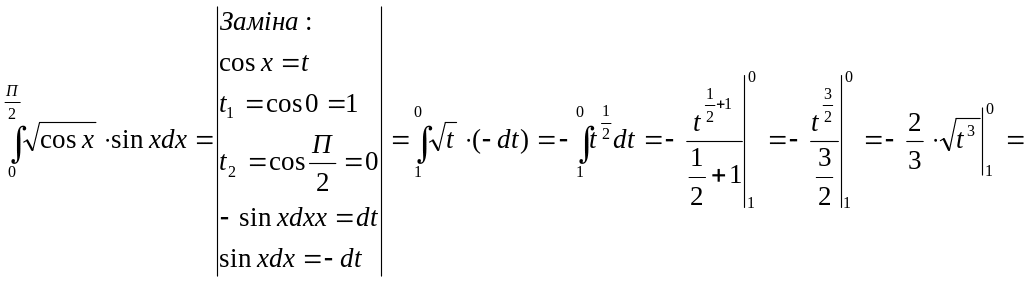