
- •Тема 1. Метрические и топологические пространства
- •Тема 3: Гильбертовы пространства
- •Тема 4 : Компактность
- •Тема 5: Линейные операторы и функционалы
- •Тема 7 : Сопряженное и второе сопряженное пространства
- •Тема 8: Элементы спектральной теории
- •Тема 8: Элементы спектральной теории
- •Тема 9 : Элементы теории обобщенных функций
Тема 4 : Компактность
Вопрос № 130
V3 |
Егер X - компакт метрикалық кеңістік болса, онда |
1 |
Ол толық және әрбір ε > 0 үшін X –те ақырлы ε-то бар |
1 |
X –тегі нүктелерінің кез келген тізбегінен жинақталатын тізбекшесі бар |
1 |
X –тегі кез келген ақырсыз жиынның кемінде бір шектік нүктесі бар |
0 |
Ол толық емес |
0 |
X –тегі кез келген ақырсыз жиынның шектік нүктесі жоқ |
0 |
Қанда да бір ε > 0 үшін Х –тің сәйкес ε-торы табылмай қалуы мүмкін |
0 |
Ол Гильберт кеңістігі |
0 |
Ол Евклид кеңістігі |
Вопрос № 131
V3 |
L(X, Y)= {A : X → Y | A – линейный непрерывный оператор , D(A)=X } совокупность всех линейных непрерывных операторов из Х в Y ( Х , Y – линейные нормированные пространства) - |
1 |
Линейное |
1 |
Нормированное пространство |
1 |
банахово пространство, если Y – банахово |
0 |
Не полное |
0 |
рефлексивное |
0 |
сепарабельное |
0 |
Не линейное |
0 |
гильбертово |
Вопрос № 132
V3 |
A : X → Y тұйық сызықты оператор болса, онда |
1 |
xn D(A ) , xn → x және Axn → y болатындығынан , x D(A ) және y = Ax болатындығы шығады |
1 |
оның {(x, Ax) | xD(A)} –графигі X× Y-те тұйық болады. |
1 |
егер A-1 бар болса, ол да тұйық болады |
0 |
Ол түйіндес оператор |
0 |
Ол шенелмеген оператор |
0 |
егер A-1 бар болса, ол тұйық емес болады |
0 |
Жете шенелген |
0 |
оның {(x, Ax) | xD(A)} –графигі X× Y-те ашық болады. |
Тема 5: Линейные операторы и функционалы
Вопрос № 133
V3 |
A : C[0;1] C[0; 1] болатын сызықты операторлар: |
1 |
Ax(t) = 3x(t) |
1 |
Ax(t) = dx/dt |
1 |
Ax(t) =
|
0 |
Ax(t) = x2(t) |
0 |
Ax(t) = x3(t)
|
0 |
Ax(t) = exp(x (t)) |
0 |
Ax(t) = ln x(t) |
0 |
Ax(t) = sin x(t) |
Вопрос № 134
V3 |
A : L1[-1;1] L1[-1; 1] болатын сызықты операторлар |
1 |
Ax(t) = 5x(t) |
1 |
Ax(t) = dx/dt (жалпыланған туынды) |
1 |
Ax(t) = |
0 |
Ax(t) = x2(t) |
0 |
Ax(t) = x3(t)
|
0 |
Ax(t) = exp(x (t)) |
0 |
Ax(t) = ln x(t) |
0 |
Ax(t) = sin x(t) |
Вопрос №135
V3 |
A : C[-2; 1] C[0;1] , Ax(t) = (t +1)x(1) операторының нормасы жататын аралықтар: |
1 |
[0; 2] |
1 |
[1; 3] |
1 |
[0; 4] |
0 |
[-2; 0] |
0 |
[-1; 1] |
0 |
[3; 5] |
0 |
[6; 8] |
0 |
[-5; -3] |
Вопрос № 136
V3 |
A : L2[0;3] L2[0; 3], Ax(t)=(t+2)x(t) операторының нормасы жататын аралықтар: |
1 |
[0; 5] |
1 |
[0; 7] |
1 |
[2; 6] |
0 |
[10; 15] |
0 |
[7; 9] |
0 |
[12; 13] |
0 |
[-1; 1] |
0 |
[-9; -3] |
Вопрос №137
V3 |
А : L2[0;4] L2[0;4] , Ax(t)=x(t) операторының нормасы жататын аралықтар:
|
1 |
[0;1] |
1 |
[0; 2] |
1 |
[1; 2] |
0 |
[-1;0] |
0 |
[-5; -2] |
0 |
[10; 15] |
0 |
[5; 10] |
0 |
[3; 10] |
Вопрос №138
V1 |
А: C[0;1]
операторы Ax(t)=0,3x(t) теңдігімен берілген болса, онда
|
1 |
оның кері операторы бар
|
1 |
оның ядросы нөлдік элементтен ғана тұрады
|
1 |
оның нормасы 0,3-ке тең
|
0 |
оның нормасы 3-ке тең
|
0 |
оның нормасы 7-ге тең |
0 |
ол шенелмеген |
0 |
ол үзілісті оператор |
0 |
ол сызықты оператор емес |
Вопрос №139
V1 |
C[0;2] кеңістігінде функционал f (x) =2x(0) теңдігімен берілген болса, онда
|
1 |
оның нормасы 2-ге тең.
|
1 |
ол шенелген функционал
|
1 |
ол x(t) =cos(t) элементіне 2 мәнін сәйкес қояды |
0 |
оның нормасы 1-ге тең
|
0 |
оның нормасы 3-ке тең |
0 |
ол үзілісті болады |
0 |
ол теріс мән қабылдай алмайды |
0 |
ол сызықты функционал емес |
Вопрос №140
V1 |
C[0;1] кеңістігінде функционал f (x) =x(0) - x(1) теңдігімен берілген болса, онда
|
1 |
оның нормасы 2-ге тең.
|
1 |
ол шенелген функционал
|
1 |
ол x(t) =cos(t) элементіне 1 - cos(1) мәнін сәйкес қояды |
0 |
оның нормасы 5-ке тең
|
0 |
оның нормасы 3-ке тең |
0 |
ол үзілісті болады |
0 |
ол теріс мән қабылдай алмайды |
0 |
ол сызықты функционал емес |
Вопрос №141
V1 |
C[0;2] кеңістігінде функционал
|
1 |
оның нормасы 2-ге тең.
|
1 |
ол шенелген функционал
|
1 |
ол x(t) =cos(t) элементіне sin (2) мәнін сәйкес қояды |
0 |
оның нормасы 3-ке тең
|
0 |
оның нормасы 3-ке тең |
0 |
ол үзілісті болады |
0 |
ол теріс мән қабылдай алмайды |
0 |
Ол сызықты функционал емес |
Вопрос №142
V1 |
C[0;1] кеңістігінде функционал
|
1 |
оның нормасы 2-ге тең.
|
1 |
ол шенелген функционал
|
1 |
ол x(t) =t элементіне 1,25 мәнін сәйкес қояды |
0 |
оның нормасы 4-ке тең
|
0 |
оның нормасы 3-ке тең |
0 |
ол үзілісті болады |
0 |
ол теріс мән қабылдай алмайды |
0 |
ол сызықты функционал емес |
Вопрос № 143
V3 |
C[0;2]
кеңістікте
анықталған
f(x)=
|
1 |
[0; 2] |
1 |
[1; 3] |
1 |
[0; 4] |
0 |
[-2; 0] |
0 |
[-1; 1] |
0 |
[3; 5] |
0 |
[6; 8] |
0 |
[-5; -3] |
Вопрос № 144
V3 |
C[0;2] кеңістікте анықталған f(x)= x(0) функционалының нормасы жататын аралықтар: |
1 |
[0;1] |
1 |
[0; 2] |
1 |
[1; 2] |
0 |
[-1;0] |
0 |
[-5; -2] |
0 |
[10; 15] |
0 |
[5; 10] |
0 |
[3; 10] |
Вопрос № 145
V3 |
C[0;2] кеңістікте анықталған f(x)= 5x(1) функционалының нормасы жататын аралықтар: |
1 |
[0;5] |
1 |
[3; 10] |
1 |
[5; 9] |
0 |
[-1;0] |
0 |
[-5; -2] |
0 |
[10; 15] |
0 |
[25; 27] |
0 |
[-3; 1] |
Вопрос № 146
V3 |
C[0;3]
кеңістікте анықталған f(x)=
|
1 |
[0; 8] |
1 |
[7; 9] |
1 |
[6; 10] |
0 |
[10; 15] |
0 |
[27; 30] |
0 |
[12; 13] |
0 |
[-1; 1] |
0 |
[-9; -3] |
Вопрос № 147
V3 |
L2[0;4]
кеңістікте анықталған f(x)=
|
1 |
[0; 7] |
1 |
[3; 9] |
1 |
[5; 10] |
0 |
[10; 15] |
0 |
[8; 9] |
0 |
[12; 13] |
0 |
[-1; 1] |
0 |
[-9; -3] |


 L2
[0;1]
L2
[0;1]
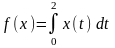 теңдігімен берілген болса,
онда
теңдігімен берілген болса,
онда теңдігімен берілген болса,
онда
теңдігімен берілген болса,
онда функционалының
нормасы
жататын
аралықтар:
функционалының
нормасы
жататын
аралықтар: функционалының нормасы жататын
аралықтар:
функционалының нормасы жататын
аралықтар: функционалының нормасы жататын
аралықтар:
функционалының нормасы жататын
аралықтар: