
- •Тема 1. Метрические и топологические пространства
- •Тема 3: Гильбертовы пространства
- •Тема 4 : Компактность
- •Тема 5: Линейные операторы и функционалы
- •Тема 7 : Сопряженное и второе сопряженное пространства
- •Тема 8: Элементы спектральной теории
- •Тема 8: Элементы спектральной теории
- •Тема 9 : Элементы теории обобщенных функций
2 уровень
Тема 1. Метрические и топологические пространства
Вопрос № 76
V3 |
Метрикалық кеңістік туралы ақиқат сөйлемдер: |
1 |
Толық метрикалық кеңістік еш жерде тығыз емес жиындардың саналымды бірігуі түрінде бейлене алмайды |
1 |
Метрикалық кеңістікте ашық жиындардың саналымды базасы бар болу үшін ( яғни екінші саналымдылық аксимасы орындалуы үшін ) ол сепарабель кеңістік болуы қажет |
1 |
Метрикалық кеңістікте ашық жиындардың саналымды базасы бар болу үшін ( яғни екінші саналымдылық аксимасы орындалуы үшін ) ол сепарабель кеңістік болуы жеткілікті |
0 |
Әрбір Метрикалық кеңістік сепарабель болады |
0 |
Кез келген топологиялық кеңістіктің топологиясы қандай да бір метрика арқылы беріледі |
0 |
Әрбір Метрикалық кеңістік толық болады |
0 |
Әрбір Метрикалық кеңістіктің жиын ретіндегі қуаты контиуум |
0 |
Әрбір Метрикалық кеңістік саналымды жиын болады |
Вопрос № 77
V3 |
Метрикалық кеңістік туралы ақиқат сөйлемдер: |
1 |
метрикалық кеңістік толық болуы үшін онда енгізілген шарлар принципі орындалуы қажет және жеткілікті |
1 |
(X, d) метрикалық кеңістікте xnx, yny (n) болса, онда d(xn, yn)d(x,y) |
1 |
Шенелген сандық тізбектер кеңістігі m сепарабель емес |
0 |
Әрбір Метрикалық кеңістік сепарабель болады |
0 |
Кез келген топологиялық кеңістіктің топологиясы қандай да бір метрика арқылы беріледі |
0 |
Әрбір Метрикалық кеңістік толық болады |
0 |
Әрбір Метрикалық кеңістіктің жиын ретіндегі қуаты контиуум |
0 |
Әрбір Метрикалық кеңістік саналымды жиын болады |
Вопрос № 78
V3 |
Метрикалық кеңістік туралы ақиқат сөйлемдер: |
1 |
метрикалық кеңістік толық болуы үшін онда енгізілген шарлар принципі орындалуы қажет және жеткілікті |
1 |
(X, d) метрикалық кеңістікте xnx, yny (n) болса, онда d(xn, yn)d(x,y) |
1 |
Шенелген сандық тізбектер кеңістігі m сепарабель емес |
0 |
Әрбір Метрикалық кеңістік сепарабель болады |
0 |
Кез келген топологиялық кеңістіктің топологиясы қандай да бір метрика арқылы беріледі |
0 |
Әрбір Метрикалық кеңістік толық болады |
0 |
Әрбір Метрикалық кеңістіктің жиын ретіндегі қуаты контиуум |
0 |
Әрбір Метрикалық кеңістік саналымды жиын болады |
Вопрос № 79
V3 |
Метрикалық кеңістік туралы ақиқат сөйлемдер: |
1 |
метрикалық кеңістікте әрбір фундаменталь тізбек шенелген болады |
1 |
(X, d) метрикалық кеңістікте {xn} және {yn } фундаменталь тізбектер болса, онда d(xn, yn) сандық тізбегі жинақталады |
1 |
(X, d) метрикалық кеңістікте xnx (n) болса, онда әрбір yX үшін d(xn, y)d(x,y) (n). |
0 |
Әрбір Метрикалық кеңістік сепарабель болады |
0 |
Кез келген топологиялық кеңістіктің топологиясы қандай да бір метрика арқылы беріледі |
0 |
Әрбір Метрикалық кеңістік толық болады |
0 |
Әрбір Метрикалық кеңістіктің жиын ретіндегі қуаты контиуум |
0 |
Әрбір Метрикалық кеңістік саналымды жиын болады |
Вопрос № 80
V3 |
Бос емес X жиынында d метрикасы әртүрлі x, y элементтері үшін d(x,y)=1, ал әрбір х үшін d(x,x)=0 деп анықталсын. Ақиқат сөйлемдер: |
1 |
Бұл кеңістіктегі әрбір тізбек шенелген болады |
1 |
Бұл кеңістікте тек қана белгілі бір нөмірден бастап тұрақты болатын тізбектер ғана жинақталады |
1 |
Бұл кеңістікте кез келген жиын ашық болады |
0 |
Бұл сепарабель кеңістік болады |
0 |
Бұл кеңістікте ашық емес жиындар бар |
0 |
Бұл кеңістікте тұйық емес жиындар бар |
0 |
Бұл кеңістіктегі нүктелер саны ақырлы |
0 |
Беріліп тұрған d метрика болмайды. |
Вопрос № 81
V3 |
Бос емес X жиынында d метрикасы әртүрлі x, y элементтері үшін d(x,y)=1, ал әрбір х үшін d(x,x)=0 деп анықталсын. Ақиқат сөйлемдер: |
1 |
Бұл кеңістікте шенелмеген тізбек жоқ |
1 |
Бұл кеңістік толық |
1 |
Бұл кеңістікте кез келген жиын тұйық болады |
0 |
Бұл сепарабель кеңістік болады |
0 |
Бұл кеңістікте ашық емес жиындар бар |
0 |
Бұл кеңістікте тұйық емес жиындар бар |
0 |
Бұл кеңістіктегі нүктелер саны ақырлы |
0 |
Беріліп тұрған d метрика болмайды. |
Вопрос № 81
V3 |
Метрикалық кеңістік туралы ақиқат сөйлемдер: |
1 |
метрикалық кеңістіктегі әрбір фундаменталь тізбек жинақталатын болса, онда ол толық кеңістік |
1 |
(X, d) толық емес метрикалық кеңістік болса, онда ол кеңістікте қиылысуы бос болатын радиустары нөлге ұмтылатын енгізілген тұйық шарлар тізбегі бар |
1 |
(X, d) толық емес метрикалық кеңістік болса, онда қысып бейнелеу принципі орындалмай қалуы мүмкін |
0 |
Әрбір Метрикалық кеңістік сепарабель болады |
0 |
Кез келген топологиялық кеңістіктің топологиясы қандай да бір метрика арқылы беріледі |
0 |
Әрбір Метрикалық кеңістік толық болады |
0 |
Әрбір Метрикалық кеңістіктің жиын ретіндегі қуаты контиуум |
0 |
Әрбір Метрикалық кеңістік саналымды жиын болады |
Вопрос № 82
V3 |
Метрикалық кеңістік туралы ақиқат сөйлемдер: |
1 |
(X, d) метрикалық кеңістік толық болса, онда әрбір A: XX қысып бейнелейтін операторының қозмғалайтын нүктесі бар және жалғыз. |
1 |
(X, d) метрикалық кеңістікте X ақырлы жиын болса, онда бұл толық кеңістік болады. |
1 |
(X, d) толық емес метрикалық кеңістік болса да, қозғалмайтын нүктесі бар A: XX операторы табылады. |
0 |
Әрбір Метрикалық кеңістік сепарабель кеңістік болады |
0 |
Кез келген топологиялық кеңістіктің топологиясы қандай да бір метрика арқылы беріледі |
0 |
Әрбір Метрикалық кеңістік толық болады |
0 |
Әрбір Метрикалық кеңістіктің жиын ретіндегі қуаты контиуум |
0 |
Әрбір Метрикалық кеңістік саналымды жиын болады |
Вопрос № 83
V3 |
Метрикалық кеңістік туралы ақиқат сөйлемдер: |
1 |
(X, d) метрикалық кеңістік хаусдорф кеңістігі де болады |
1 |
(X, d) метрикалық кеңістікте бірінші бөліктеу аксиомасы орындалады |
1 |
(X, d) метрикалық кеңістік нормал кеңістік те болады |
0 |
Әрбір Метрикалық кеңістік сепарабель кеңістік болады |
0 |
Кез келген топологиялық кеңістіктің топологиясы қандай да бір метрика арқылы беріледі |
0 |
Әрбір Метрикалық кеңістік толық болады |
0 |
Әрбір Метрикалық кеңістіктің жиын ретіндегі қуаты контиуум |
0 |
Әрбір Метрикалық кеңістік саналымды жиын болады |
Вопрос № 84
V3 |
(X, ) топологиялық кеңістік болсын. Онда |
1 |
ашық жиындар жүйесіне бос жиын да кіреді |
1 |
ашық жиындар жүйесіне Х те кіреді |
1 |
ашық жиындар жүйесі бірігу амалына қатысты тұйық |
0 |
ашық жиындар жүйесі ақырсыз қиылысу амалына қатысты тұйық |
0 |
Х тұйық жиын болмайды |
0 |
Бос жиын тұйық емес |
0 |
(X, ) топологиялық кеңістікте тізбектің жинақтылығы деген ұғым анықталмаған |
0 |
(X, ) топологиялық кеңістікте тұйық жиын деген ұғым болмайды |
Вопрос № 85
V3 |
(X, ) топологиялық кеңістік болсын. Ақиқат сөйлемдер: |
1 |
G болса, онда Х\G тұйық деп аталады |
1 |
G1 және G2 болса, онда G1G2 |
1 |
G1 және G2 болса, онда G1G2 |
0 |
ашық жиындар жүйесі ақырсыз қиылысу амалына қатысты тұйық |
0 |
Х тұйық жиын болмайды |
0 |
Бос жиын тұйық емес |
0 |
(X, ) топологиялық кеңістікте тізбектің жинақтылығы деген ұғым анықталмаған |
0 |
(X, ) топологиялық кеңістікте тұйық жиын деген ұғым болмайды |
Вопрос № 86
V3 |
(X, ) топологиялық кеңістік болсын. Ақиқат сөйлемдер: |
1 |
Егер әртүрлі x және у элементтері үшін хG1 , уG1 және хG2 , уG2 шарттарын қанағаттандыратын G1 және G2 бар болса, ондабірінші бөліктену аксимасы орындалады дейді |
1 |
Егер әртүрлі x және у элементтері үшін хG1, уG2 және G1G2= шарттарын қанағаттандыратын G1 және G2 бар болса, онда екінші бөліктену аксимасы орындалады дейді |
1 |
Егер кез келген екі қиылыспайтын екі тұйық жиын үшін олардың өзара қиылыспайтын екі маңайлары бар болса, онда (X, ) нормал кеңістік дейді |
0 |
ашық жиындар жүйесі ақырсыз қиылысу амалына қатысты тұйық |
0 |
Х тұйық жиын болмайды |
0 |
Бос жиын тұйық емес |
0 |
(X, ) топологиялық кеңістікте тізбектің жинақтылығы деген ұғым анықталмаған |
0 |
(X, ) топологиялық кеңістікте тұйық жиын деген ұғым болмайды |
Вопрос № 87
V3 |
(X, ) топологиялық кеңістіктер болсын (І). Ақиқат сөйлемдер: |
1 |
жүйесі де Х-те топология болады |
1 |
жүйесі топологияларының бәрінен әлсіз болады |
1 |
Егер Х-тің қандайда бір жиыншаларынан тұратын В жүйесі берілсе, онда оны қамтитын ең әлсіз топология бар болады |
0 |
ашық жиындар жүйесі ақырсыз қиылысу амалына қатысты тұйық |
0 |
жүйесі де Х-те топология болады |
0 |
Бос жиын тұйық емес |
0 |
(X, ) топологиялық кеңістікте тізбектің жинақтылығы деген ұғым анықталмаған |
0 |
(X, ) топологиялық кеңістікте тұйық жиын деген ұғым болмайды |
Вопрос № 88
V3 |
Кеңістіктегі топология және оның базасы туралы ақиқат сөйлемдер: |
1 |
Ашық жиындардың қандай да бір жүйесі J={G| І } берілген топологиясының базасы болу үшін әрбір х элемент пен оның кез келген G маңайы үшін х Gх G болатын GхJ табылатын болуы қажет және жеткілікті |
1 |
Метрикалық кеңістікте барлық ашық шарлар жүйесі база болады |
1 |
Саналымды базасы бар топологиялық кеңістіктер бар |
0 |
ашық жиындар жүйесі ақырсыз қиылысу амалына қатысты тұйық |
0 |
Базасы жоқ топология болады |
0 |
Барлық топологияның саналымды базасы болады |
0 |
(X, ) топологиялық кеңістікте тізбектің жинақтылығы деген ұғым анықталмаған |
0 |
(X, ) топологиялық кеңістікте тұйық жиын деген ұғым болмайды |
Вопрос № 89
V3 |
C[0;1] кеңістігінде ара қашықтығы 1 –ге тең элементтер: |
1 |
x(t)=2t; y(t) = t |
1 |
x(t)=t2 ; y(t) = 2t -1 |
1 |
x(t)=t +1; y(t) = 1 |
0 |
x(t)=3t; y(t) = t |
0 |
x(t)=t-1; y(t) = t +1 |
0 |
x(t)=t; y(t) = 5; |
0 |
x(t)=2t +3; y(t) = t-1 |
0 |
x(t)=4t; y(t) = 2t-5 |
Вопрос № 90
V3 |
C[-1;1] кеңістігінде ара қашықтығы 2–ге тең элементтер: |
1 |
x(t)=2t + 1; y(t) = t |
1 |
x(t)=t ; y(t) = 2t -1 |
1 |
x(t)=t -1; y(t) = t +1 |
0 |
x(t)=2t; y(t) = t |
0 |
x(t)=2t-1; y(t) = t +3 |
0 |
x(t)=t; y(t) = 5; |
0 |
x(t)=2t + 3; y(t) = t-1 |
0 |
x(t)=4t; y(t) = 2t-5 |
Вопрос № 91
V3 |
C[0;1] кеңістігінде ара қашықтығы 3 –ке тең элементтер: |
1 |
x(t)=4t; y(t) = t |
1 |
x(t)=t +1 ; y(t) = t -2 |
1 |
x(t)=t +3; y(t) = 1 |
0 |
x(t)=3t; y(t) = t |
0 |
x(t)=t-1; y(t) = t +1 |
0 |
x(t)=t; y(t) = 5; |
0 |
x(t)=2t+3; y(t) = t-1 |
0 |
x(t)=4t; y(t) = 2t-5 |
Вопрос № 92
V3 |
C[-1;1] кеңістігінде ара қашықтығы 4 –ке тең элементтер: |
1 |
x(t)=5t; y(t) = t |
1 |
x(t)=2t + 2 ; y(t) = 2t -2 |
1 |
x(t)=6t +1; y(t) = 2t + 1 |
0 |
x(t)=3t; y(t) = t |
0 |
x(t)=t-1; y(t) = t +1 |
0 |
x(t)=t; y(t) = 8; |
0 |
x(t)=2t+3; y(t) = t-1 |
0 |
x(t)=4t; y(t) = 2t + 5 |
Вопрос № 93
V3 |
L1[0;1] кеңістігінде ара қашықтығы 1 –ге тең элементтер: |
1 |
x(t)=3t; y(t) = t |
1 |
x(t)=2t + 2 ; y(t) = 2 |
1 |
x(t)=t +2; y(t) = t + 1 |
0 |
x(t)=t; y(t) =1 |
0 |
x(t)=t-1; y(t) = t +1 |
0 |
x(t)=t; y(t) = 8; |
0 |
x(t)=2t+3; y(t) = t-1 |
0 |
x(t)=4t; y(t) = 2t + 5 |
Вопрос № 94
V3 |
L1[0;1]кеңістігінде ара қашықтығы 2 –ге тең элементтер: |
1 |
x(t)=2t +1; y(t) = 1-2t |
1 |
x(t)=6t + 2 ; y(t) = 2t + 2 |
1 |
x(t)=t + 1; y(t) = t – 1 |
0 |
x(t)=t; y(t) =1 |
0 |
x(t)=3t-1; y(t) = t +1 |
0 |
x(t)=t; y(t) = 8; |
0 |
x(t)=2t+3; y(t) = t-1 |
0 |
x(t)=4t; y(t) = 2t + 5 |
Вопрос № 95
V3 |
L2[0;1]кеңістігінде ара қашықтығы 1 –ден кіші элементтер: |
|
x(t) =t ; y(t) = 1 |
1 |
x(t) =2t ; y(t) = t |
1 |
x(t) =2t ; y(t) = t + 1 |
0 |
x(t)=t +1; y(t) =t-1 |
0 |
x(t)=5t; y(t) = t |
0 |
x(t)=3t+1; y(t) =1; |
0 |
x(t)=2t+3; y(t) = t-1 |
0 |
x(t)=4t; y(t) = 4t + 6 |
Вопрос № 96
V3 |
L2[0;1] кеңістігінде ара қашықтығы 1 –ден үлкен элементтер: |
1 |
x(t)=t +1; y(t) =t-1 |
1 |
x(t)=5t; y(t) = t |
1 |
x(t)=3t+1; y(t) =1; |
0 |
x(t) =t ; y(t) = 1 |
0 |
x(t) =2t ; y(t) = t |
0 |
x(t) =2t ; y(t) = t + 1 |
0 |
x(t)=4t; y(t) = 4t -1 |
0 |
x(t)=2t + 3; y(t) = 2t +2 |
Вопрос № 97
V3 |
m кеңістігінде ара қашықтығы 3 –ке тең элементтер: |
1 |
(4,2,4,2,4,2,…); (1,2,1,2,1,2,…) |
1 |
(1,2,1,2,1,2,…); (-2; 2; -2; 2;-2,2,-2,…) |
1 |
(5,0,5,0,5,0,..); (2,1,2,1,2,1,…) |
0 |
(1,-1,1,-1,1,-1,..);(7,-7,7,-7,7,-7,…) |
0 |
(1,1/2,1/3,1/4,..);(1/2,1/3,1/4,…) |
0 |
(1,-1,1,-1,1,-1,..);(2,2,2,2…) |
0 |
(3,-1,3,-1,3,..);(7,-7,7,-7,7,-7,…) |
0 |
(0,-1,0,-1,0,-1,..);(1,0,1,0,1,…) |
Вопрос № 98
V3 |
C[0;1]
кеңістігінде центрі нөлде және радиусы
1-ге тең
|
1 |
-0,7+ t |
1 |
0,5t |
1 |
0,5-t |
0 |
5t |
0 |
9-t |
0 |
10t-5 |
0 |
-t-1 |
0 |
-3t |
Вопрос № 99
V3 |
m кеңістігінде центрі нөлде және радиусы 1-ге тең ашық шарда жататын элементтер: |
1 |
(1/2,1/4,1/8,…) |
1 |
( ½, 1/3, ¼,…) |
1 |
(1/5,1/25,1/125,…) |
0 |
(2,2,2,2,…) |
0 |
(1,3,1,3,1,…) |
0 |
(7,7,7,7,7,…) |
0 |
(4,-4,4,-4,4,…) |
0 |
(8,2,8,2,8,..) |
Вопрос № 100
V3 |
C[0;1]
кеңістігінде
|
1 |
-t |
1 |
1-t |
1 |
Sin πt |
0 |
5t |
0 |
7t-1 |
0 |
10t -3 |
0 |
5+t |
0 |
14t-2 |
Вопрос № 101
V3 |
m кеңістігінде тұйық шарда жататын элементтер: |
1 |
(1,1/2,1/3,1/4,..) |
1 |
(1,-1,1,-1,…) |
1 |
(1/3,1/9,1/27,…) |
0 |
(1,2,1,2,1,2…) |
0 |
(3, 3,3,3,…) |
0 |
(2,1,1/2,1/4,…) |
0 |
(5,-5,5,-5,…) |
0 |
(7, 1, 7,1,7,…) |
Вопрос № 102
V3 |
x(t) = 3t+1 және y(t) = t+1 элементтерінің C[0;2] кеңістігіндегі ара қашықтығы жататын аралықтар : |
1 |
[-4; 4] |
1 |
[ 0; 5] |
1 |
[3; 6] |
0 |
[-1; 0] |
0 |
[2; 3] |
0 |
[0; 1] |
0 |
(-2; -1) |
0 |
(-0,5; 0,5) |
Вопрос № 103
V3 |
x(t) = 2t+1 және y(t) = t+1 элементтерінің C-4;2] кеңістігіндегі ара қашықтығы жататын аралықтар : |
1 |
[-4; 4] |
1 |
[ 0; 5] |
1 |
[3; 6] |
0 |
[-1; 0] |
0 |
[2; 3] |
0 |
[0; 1] |
0 |
(-2; -1) |
0 |
(-0,5; 0,5) |
Вопрос № 104
V3 |
x(t) = 3t+1 және y(t) = 1-2t элементтерінің C[0;1] кеңістігіндегі ара қашықтығы жататын аралықтар : |
1 |
[-5; 5] |
1 |
[ 0; 5] |
1 |
[3; 6] |
0 |
[-1; 0] |
0 |
[2; 3] |
0 |
[0; 1] |
0 |
(-2; -1) |
0 |
(-0,5; 0,5) |
Вопрос № 105
V3 |
x(t) = 2t+1 және y(t) = t+1 элементтерінің L1[-1;1] кеңістігіндегі ара қашықтығы жататын аралықтар : |
1 |
[-1; 1] |
1 |
[ 0; 2] |
1 |
[1; 3] |
0 |
[-1; 0] |
0 |
[2; 3] |
0 |
[10; 15] |
0 |
(-2; -1) |
0 |
(-0,5; 0,5) |
Вопрос № 106
V3 |
x(t) = 3t+2 және y(t) = t+1 элементтерінің L1[0;1] кеңістігіндегі ара қашықтығы жататын аралықтар : |
1 |
[-2;2] |
1 |
[ 0; 3] |
1 |
[1; 3] |
0 |
[-1; 0] |
0 |
[12; 15] |
0 |
[0; 1] |
0 |
(-2; -1) |
0 |
(-0,5; 0,5) |
Вопрос № 107
V3 |
x(t) = 5t-1 және y(t) = t-1 элементтерінің L1[0;2] кеңістігіндегі ара қашықтығы жататын аралықтар : |
1 |
[-2;2] |
1 |
[ 0; 3] |
1 |
[1; 3] |
0 |
[-1; 0] |
0 |
[12; 15] |
0 |
[0; 1] |
0 |
(-2; -1) |
0 |
(-0,5; 0,5) |
Вопрос № 108
V3 |
x(t) = 3t+1 және y(t) = t+1 элементтерінің L2[-1;1] кеңістігіндегі ара қашықтығы жататын аралықтар : |
1 |
[-2; 2] |
1 |
[ 0; 2] |
1 |
[1; 3] |
0 |
[-1; 0] |
0 |
[2; 3] |
0 |
[0; 1] |
0 |
(-2; -1) |
0 |
(-0,5; 0,5) |
Вопрос № 109
V3 |
x(t) = 6t+1 және y(t) = 2t+1 элементтерінің L2[0;1] кеңістігіндегі ара қашықтығы жататын аралықтар : |
1 |
[-3;3] |
1 |
[ 0; 3] |
1 |
[2; 4] |
0 |
[-1; 0] |
0 |
[0; 1] |
0 |
[15; 20] |
0 |
(-2; -1) |
0 |
(-0,5; 0,5) |
Вопрос № 110
V3 |
x
=(1,1/2, ¼,1/8, …) және
y =(1/2,1/4,
1/8,…) элементтерінің
|
1 |
[-1;1] |
1 |
[ 0; 2] |
1 |
[1; 3] |
0 |
[-1; 0] |
0 |
[2; 3] |
0 |
[5; 10] |
0 |
(-2; -1) |
0 |
(-0,5; 0,5) |
Вопрос № 111
V3 |
x =( 2/3, 2/9, 2/27 ,…) және y =(1/3,1/9,1/27 ,…) элементтерінің кеңістігіндегі ара қашықтығы жататын аралықтар : |
1 |
[-1; 1] |
1 |
[ 0; 2] |
1 |
[0,5; 1] |
0 |
[-1; 0] |
0 |
[2; 3] |
0 |
[10; 15] |
0 |
(-2; -1) |
0 |
(4; 6) |
Вопрос № 112
V3 |
x =(2/5, 2/25, 2/125, …) және y =(1/5, 1/25, 1/125, …) элементтерінің кеңістігіндегі ара қашықтығы жататын аралықтар : |
1 |
[-1; 1] |
1 |
[ 0; 1] |
1 |
[-0,5; 0,5 ] |
0 |
[-1; 0] |
0 |
[2; 3] |
0 |
[10; 15] |
0 |
(-2; -1) |
0 |
(4; 6) |
Вопрос № 113
V3 |
x
=(1,1/2, ¼,1/8, …) және
y =(1/2,1/4,
1/8,…) элементтерінің
|
1 |
[-1;1] |
1 |
[ 0; 2] |
1 |
[1; 3] |
0 |
[-1; 0] |
0 |
[2; 3] |
0 |
[5; 10] |
0 |
(-2; -1) |
0 |
(-0,5; 0,5) |
Вопрос № 114
V3 |
x =( 2/3, 2/9, 2/27 ,…) және y =(1/3,1/9,1/27 ,…) элементтерінің кеңістігіндегі ара қашықтығы жататын аралықтар : |
1 |
[-1; 1] |
1 |
[ 0; 1] |
1 |
[0,1; 0,6] |
0 |
[-1; 0] |
0 |
[2; 3] |
0 |
[10; 15] |
0 |
(-2; -1) |
0 |
(4; 6) |
Вопрос № 115
V3 |
x =(2/5, 2/25, 2/125, …) және y =(1/5, 1/25, 1/125, …) элементтерінің кеңістігіндегі ара қашықтығы жататын аралықтар : |
1 |
[-1; 1] |
1 |
[ 0; 1] |
1 |
[-0,5; 0,5 ] |
0 |
[-1; 0] |
0 |
[2; 3] |
0 |
[10; 15] |
0 |
(-2; -1) |
0 |
(4; 6) |
Вопрос № 116
V3 |
x =(1/5, 1/25, 1/125,…) және y =(1, 1/5, 1/25, 1/125, ,…) элементтерінің m барлық шенелген тізбектер кеңістігіндегі ара қашықтығы жататын аралықтар : |
1 |
[-1; 1] |
1 |
[ 0; 1] |
1 |
[-0,5; 0,5 ] |
0 |
[-1; 0] |
0 |
[2; 3] |
0 |
[10; 15] |
0 |
(-2; -1) |
0 |
(4; 6) |
Вопрос № 117
V3 |
x =(1, ½, 1/3, ¼,,…) және y =(1/2, 1/3, ¼, 1/5,…) элементтерінің m барлық шенелген тізбектер кеңістігіндегі ара қашықтығы жататын аралықтар : |
1 |
[-1; 1] |
1 |
[ 0; 1] |
1 |
[-0,5; 0,5 ] |
0 |
[-1; 0] |
0 |
[2; 3] |
0 |
[1; 6] |
0 |
(-2; -1) |
0 |
(4; 6) |
Вопрос № 118
V3 |
C[0;1] кеңістігінде M={x(t)
жиыны және y(t)= t элементі берілсін. Онда |
1 |
у нүктесі М жиынына сыртқы нүкте |
1 |
у нүктесі М жиынына жатпайды |
1 |
М жиыны ашық жиын |
0 |
у нүктесі М жиынының ішкі нүктесі |
0 |
у нүктесі М жиынының шекаралық нүктесі |
0 |
у нүктесі М жиынының шектік нүктесі |
0 |
М жиыны тұйық жиын |
Вопрос №119
V3 |
C[0;1] кеңістікте M={x(t) C[0;1] | min x(t) >2 } жиыны және y=cos t элементі берілсін. Онда |
1 |
у нүктесінің М жиынымен қиылыспайтын қандай да бір маңайы бар |
1 |
у нүктесі М-де жатпайды |
1 |
у нүктесі М-ге шектік нүкте болмайды |
0 |
у нүктесі М-ге ішкі нүкте болады |
0 |
у нүктесі М-ге шектік нүкте болады |
0 |
мүшелері М-де жататын және у-ке ұмтылатын тізбек табылады |
0 |
Оқшауланған |
Вопрос №120
V3 |
C[-1;1] кеңістігінде M={x(t)
C[-1;1]
| max x(t)
|
1 |
y нүктесі М-де жатады
|
1 |
y нүктесі М-ге ішкі нүкте болады |
1 |
y нүктесі М-ге шектік нүкте болады |
0 |
y нүктесі М-де жатпайды
|
0 |
C[-1;1] кеңістігінде мүшелері М-де жататын және у-ке ұмтылатын тізбек табылмайды |
0 |
y нүктесі М-ге оқшауланған нүкте болады |
0 |
C[-1;1] кеңістігінде мүшелері М-де жатпайтын және у-ке ұмтылатын тізбек табылады |
0 |
У нүктесі C[-1;1] кеңістігінің элементі емес |
Вопрос №121
V3 |
С[a; b] кеңістігінде функциялық тібектің норма бойынша жинақтылығынан: |
1 |
ол тізбектің [a,b] сегментінде бірқалыпты жинақтылығы шығады |
1 |
ол тізбектің [a,b] сегментінде нүктелі жинақтылығы шығады |
1 |
ол тізбектің [a,b] сегментінде орташа квадраттық жинақтылығы шығады |
0 |
ол тізбектің [a,b] сегментінде нүктелі жинақтылығы шығады да, бірақ бірқалыпты жинақтылығы шықпайды |
0 |
ол тізбектің мүшелері нөлдік функциялар болатындығы шығады |
0 |
ол тізбектің [a,b] сегментінде нүктелі жинақтылығы шығады да, бірақ орташа квадраттық жинақтылығы шықпайды |
0 |
ол тізбектің шегі полином болатындығы шығады |
0 |
ол тізбектің шегі тригонометриялық полином болатындығы шығады |

 1
1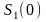 ашық
шарда
жататын элементтер:
ашық
шарда
жататын элементтер: тұйық шарда
жататын элементтер:
тұйық шарда
жататын элементтер: кеңістігіндегі
ара қашықтығы жататын аралықтар :
кеңістігіндегі
ара қашықтығы жататын аралықтар : кеңістігіндегі
ара қашықтығы жататын аралықтар :
кеңістігіндегі
ара қашықтығы жататын аралықтар : C[0;1]
| барлық t үшін x(t)
>2 }
C[0;1]
| барлық t үшін x(t)
>2 }
 1
} жиыны y(t)=0.5t нүктесі берілсін. Онда
1
} жиыны y(t)=0.5t нүктесі берілсін. Онда