Задание №4:
Используя критическое значение из задания 3 и передаточные функции из задания 1 получим:
W(S)
Ф(S)=
.
Подставив в передаточную функцию замкнутой системы вместо s=jώ, и выделив мнимую и действительную часть получим:
Re[Ф(jώ
)]=
,
Im[Ф(jώ
)]=
,
Φ(ώ)=
,
A(ώ)=
.
Таблица
3.4.1 - Значения
,
lg
,
P,
Q,
A,
20lg
A,
φ.
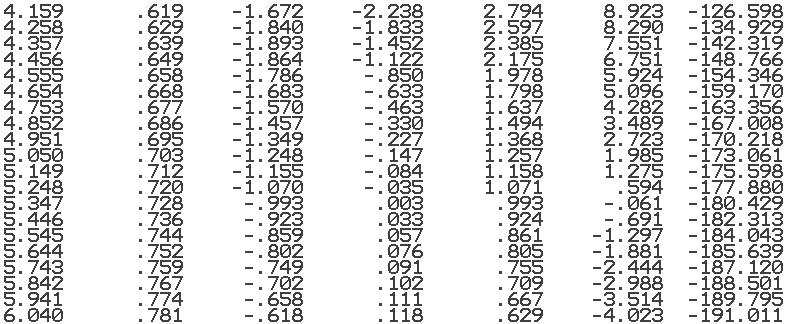
В соответствие с таблицей построим АЧХ и ФЧХ.
Рисунок 3.4.1 - АЧХ замкнутой системы
Рисунок 3.4.2 - ФЧХ замкнутой системы
Также поступим и с передаточной функцией разомкнутой системы:
Re[Ф(jώ
)]=
;
Im[Ф(jώ
)]=
;
Φ(ώ)= ,
A(ώ)= .
L(ώ)=20*lgA(ώ).
Таблица 3.4.2 - Значения P,Q,A,φ, lgώ, lgA
В соответствие с таблицей построим ЛАЧХ и ЛФХ.
Рисунок 3.4.3 - ЛАХ и ЛФХ разомкнутой системы
Из рисунка видно, что ϒ=27.4 градусов =0.4779 радиан, а Н=8,33 градус =0.1454 радиан. Из формулы (1.4.1) получим h=1.016.
Задания №5.
В соответствие с теоретической частью задания выбираем вид структурной схемы типа рисунок 3.5.1.
Рисунок 3.5.1 - Вид выбранной структурной схемы
Wку0
=
,
Wку1
=
,
Wку2
=
,
Wку3
=
.
Запишем предаточную функцию системы:
Ф(S)=
.
(3.5.1)
Подставим соответствующие передаточные функции в формулу (5.10) и получим коэффициенты знаменателя при степенях.
а4=Tiy*Toy+Ky*Tiy*Toy*κ11,
a3
=
,
a2=
a1=
,
a0=
,
Так
как a4=1,
то
.
Из условия астатизма 1-ого порядка
.
Зададимся некоторыми параметрами для
совместности системы. Приняв
,мы упростим нашу систему.
Для
определения коэффициентов желаемой
передаточной функции, найдём на основе
ОМК значения δ1,
δ2,δ3,
z=
.
И из формул 1.5.2 найдем, желаемые
коэффициенты.
Получим на основе четырех графиков ОМК 4 различных значения δ1, δ2,δ3, z и занесём в таблицу.
Таблица 3.5.1 – Значения δ1, δ2,δ3, z.
|
I |
II |
III |
IV |
δ1 |
2 |
2,8 |
2,1 |
2 |
δ2 |
1,4 |
2 |
2 |
2 |
δ3 |
1,6 |
1,4 |
1,2 |
1 |
tнн |
1,5 |
2,15 |
1,55 |
1,55 |
z |
0,24 |
0,1674419 |
0,2322581 |
0,2322581 |
Для каждого из случаев рассчитаем значения желаемых коэффициентов:
Таблица 3.5.2 – Значения а3ж, а2ж, а1ж, а0ж.
|
I |
II |
III |
IV |
a3ж |
18,666667 |
46,822222 |
21,7 |
17,222222 |
a2ж |
217,77778 |
1565,9432 |
392,40833 |
296,60494 |
a1ж |
1814,8148 |
26186,05 |
3548,0253 |
2554,0981 |
a0ж |
7561,7284 |
156388,91 |
15276,22 |
10996,811 |
Взяв значения из задания №1 и №2 , приняв α=5 составим матрицу коэффициентов СЛАУ:
1 |
0 |
0 |
54945,08 |
0 |
81400,11 |
7142,86 |
0 |
5,826211 |
11,39601 |
0 |
0 |
203500,3 |
54945,08 |
203500,3 |
81400,11 |
0 |
268,1149 |
28,49003 |
101750,1 |
0 |
0 |
203500,3 |
0 |
203500,3 |
0 |
2554,098 |
0 |
0 |
101750,1 |
0 |
0 |
0 |
0 |
101750,1 |
10996,81 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
101750,1 |
10996,81 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
5 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
(3.5.2)
Подставив получение значения в систему (3.5.2), получим 4 системы уравнений, решив которые найдём значения коэффициентов корректирующих устройств, занесем решения в таблицу.
Таблица 3.5.2 – Значения коэффициентов корректирующих устройств
|
I |
II |
III |
IV |
α |
5 |
5 |
5 |
5 |
k31 |
0,0119261 |
0,2061691 |
0,0230125 |
0,0161277 |
k30 |
0 |
0 |
0 |
0 |
k21 |
4,133E-05 |
0,0005538 |
9,653E-05 |
1,504E-05 |
k20 |
0,0022549 |
0,0248936 |
0,0052287 |
0,003787 |
k11 |
0 |
0 |
0 |
0 |
k10 |
0 |
0 |
0 |
0 |
k00 |
0,0743166 |
1,5369896 |
0,1501346 |
0,1080766 |
Выбрав из четырех случаев наименьшие значения коэффициентов корректирующих устройств, получим передаточные функции корректирующих устройств:
,
,
,
.
Точный переходный процесс имеет вид:
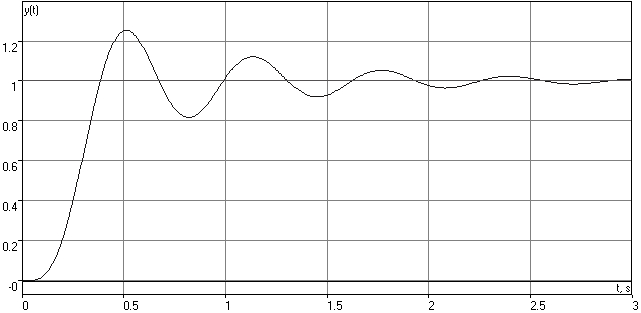
Рисунок 3.5.2 - Переходный процесс скорректированной системы
Из рисунка 3.5.2 видно, что точное время переходного процесса составляет 1.8086 с., а Ϭ=24.83%.