
- •1. Постановка задачи и исходные данные
- •1.1 Постановка задачи
- •1.2 Исходные данные
- •2. Математическая модель пространственного движения ка вокруг центра масс.
- •3. Выбор маховиков для обеспечения разворота ка на заданные углы
- •4.1. Моделирование режима разворота ка в соответствии с математической моделью, полученной в пункте 2
- •4.1.1. Исследование режима поворота ка по углу тангажа при диагональном тензоре инерции.
- •4.1.2 Исследование режима поворота ка по углу тангажа при недиагональном тензоре инерции.
- •4.1.3. Исследование режима поворота ка по углу крена при недиагональном тензоре инерции.
4.1.3. Исследование режима поворота ка по углу крена при недиагональном тензоре инерции.
Максимальная
угловая скорость

Управляющий
момент

Начальные условия:
 (18)
(18)
Получаем графики углов поворота, угловых скоростей и моментов.
Углы ориентации
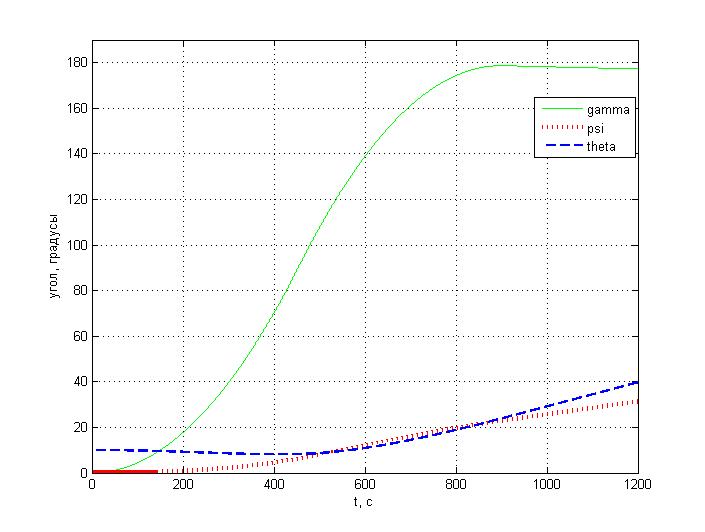
Угловые скорости

Управляющие моменты
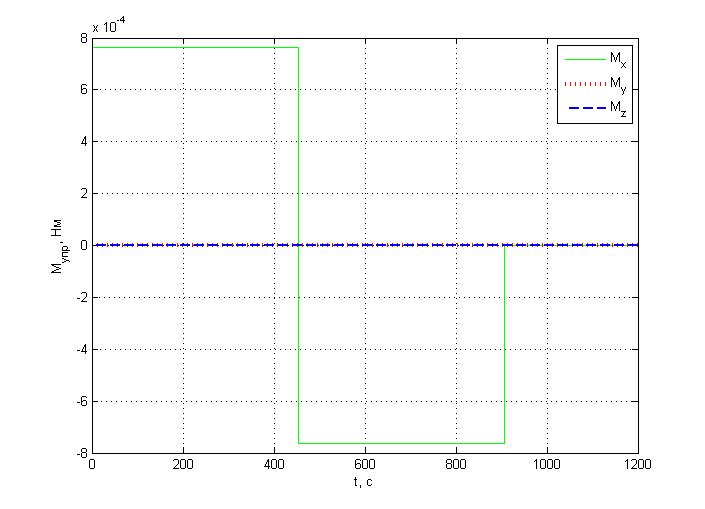
Вывод: при
недиагональном тензоре инерции при
развороте по углу крена на 1800 за
заданное время
 с,
мы получаем:
с,
мы получаем:
 ,
,
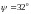 ,
,
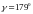 ,
,
 ,
, ,
, .
.
Гироскопический момент влияет на движение КА.
Введем моменты, которые будут стабилизировать движение КА после поворота по крену на угол 180 градусов:

Для управления по этим каналам введем сигнал управления, зависящий от угла и от скорости по каналу, и функцию управления
Сигналы управления:

Введем релейную функцию управления, зависящую от сигнала управления и определяющую знак стабилизирующего момента. Зону нечувствительности примем
Получим следующие результаты для углов, скоростей и моментов:
Углы ориентации:
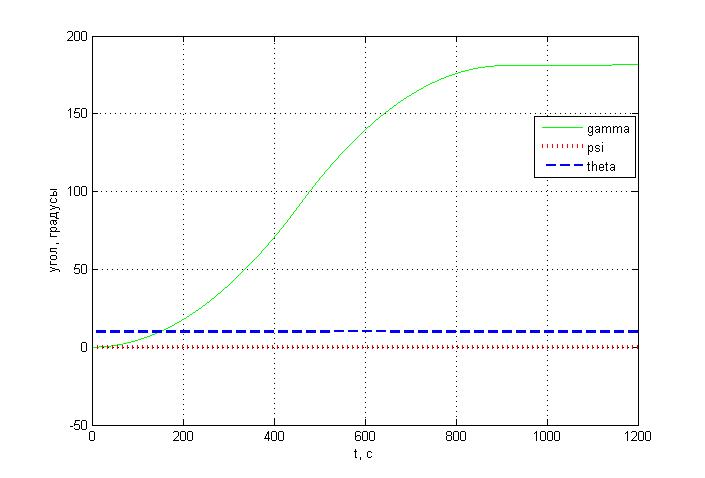
Угловые скорости:
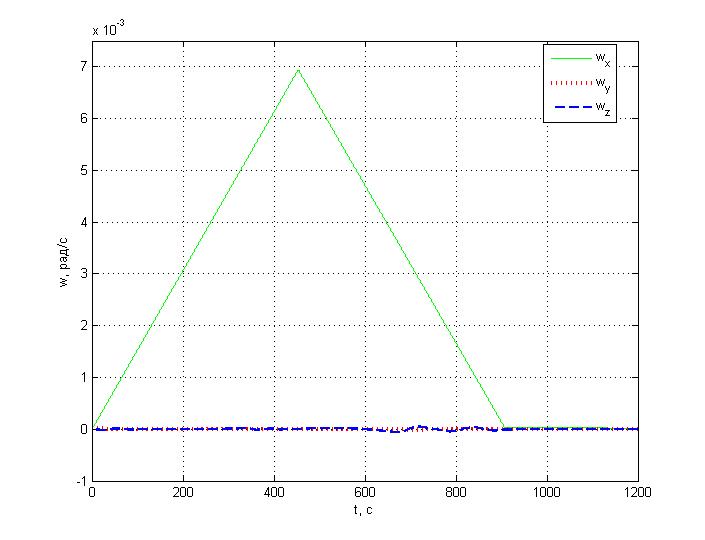
Управляющий момент:

Вывод: провели моделирование движения КА для случая недиагонального тензора инерции и ввели в систему управления моменты, которые стабилизируют движение КА после разворота по углу крена на 1800 за время 903.733 с; получили, следующие значения углов и угловых скоростей:

Рассмотрим движение КА с учетом гравитации.
Получим графики углов поворота, угловых скоростей и моментов.
Углы ориентации
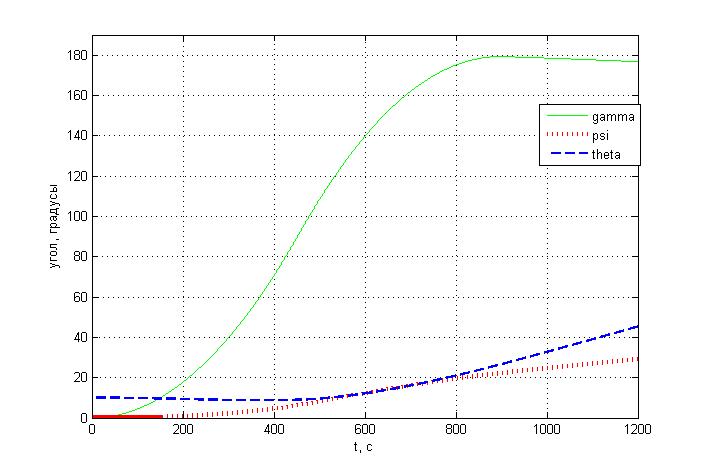
Угловые скорости:
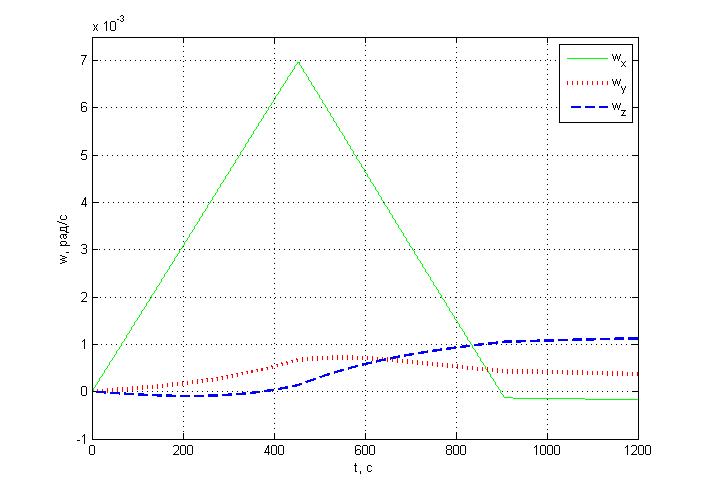
Вывод: для недиагонального тензора инерции при развороте по углу крена за заданное время
с
с учетом гравитационного момента
получаем, что КА имеет ненулевые значения
углов:
 ,
,
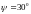 ,
,
 .Гравитационный
момент оказывает значительное влияние
на движение КА
.Гравитационный
момент оказывает значительное влияние
на движение КА
Введем моменты, которые будут стабилизировать движение КА после поворота:

Для управления по этим каналам введем сигнал управления, зависящий от угла и от скорости по каналу, и функцию управления
Сигналы управления:
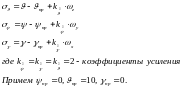
Введем релейную функцию управления, зависящую от сигнала управления и определяющую знак стабилизирующего момента. Зону нечувствительности примем
Получим следующие результаты для углов, скоростей и моментов:
Углы ориентации:
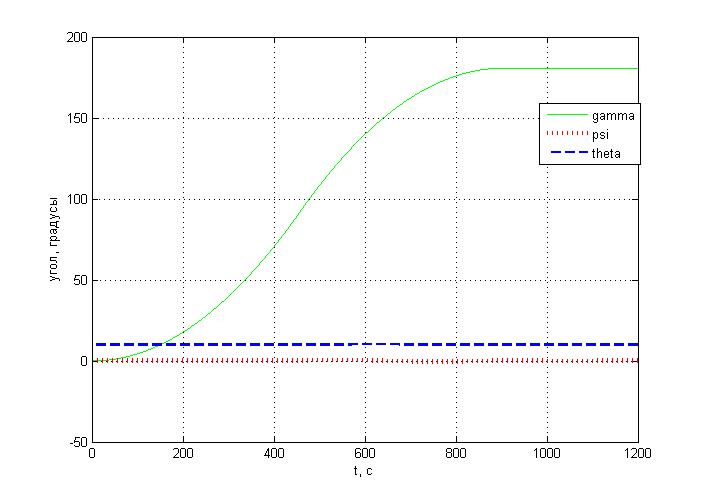
Угловые скорости:
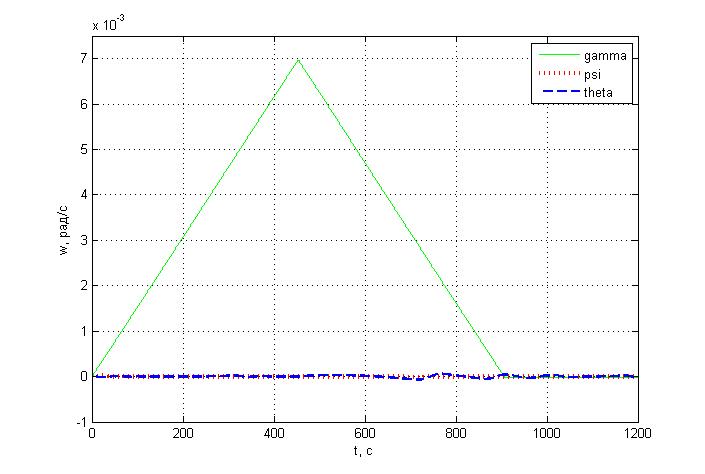
Управляющий момент:
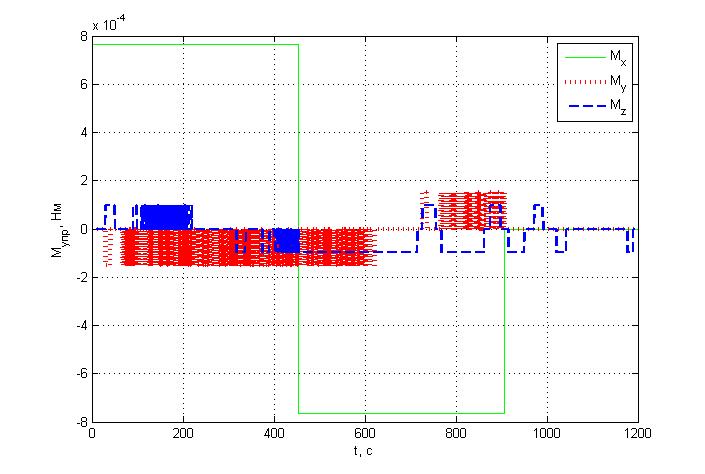
Вывод:
провели моделирование движения КА
для случая недиагонального тензора
инерции с учетом гравитации; ввели
управляющие моменты (после разворота
по углу крена) по трем канала, с
помощью которых получили следующие
значения углов ориентации:
,
,

Вывод: в данной работе составили математическую модель движения КА, подобрали маховики для обеспечения поворота КА на заданные углы и провели моделирование режимов разворота аппарата.
Влияние
центробежных моментов ( ) и гравитации оказывает большое значение
при движении КА: значения углов ориентации
для случая разворота по крену больше,
чем при развороте по тангажу:
) и гравитации оказывает большое значение
при движении КА: значения углов ориентации
для случая разворота по крену больше,
чем при развороте по тангажу:
 .
.
При
недиагональном тензоре инерции при
недиагональном тензоре инерции при
развороте по углу крена за заданное
время
 с,
мы получаем:
с,
мы получаем:
 ,
,
 ,
,
 ,
,

 ,
, ,
, ,
,
Центробежный
момент инерции
 оказывает влияние на отклонение по углу
курса в большей степени, чем на отклонение
по тангажу (
оказывает влияние на отклонение по углу
курса в большей степени, чем на отклонение
по тангажу ( ,
,
 ).
Максимальная угловая скорость
).
Максимальная угловая скорость
 осталась неизменной по сравнению с
расчетом при диагональном тензоре
инерции (
осталась неизменной по сравнению с
расчетом при диагональном тензоре
инерции (
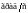 ).
Угловые скорости
).
Угловые скорости
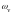 и
и
 отличны
от полученных при расчете с диагональным
тензором инерции (
отличны
от полученных при расчете с диагональным
тензором инерции ( ,
,
 ).
).
При
центробежном моменте инерции
отклонения по углам тангажа, курса и
угловая скорость
больше чем при центробежном моменте
инерции
 (
( ,
, ,
,
,
, ),
а угловая скорость
больше
(
),
а угловая скорость
больше
( )
)
Вывод: при недиагональном тензоре инерции при развороте по углу крена за заданное время с, мы получаем:
 ,
,
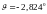 ,
,
 ,
,
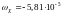 ,
, ,
,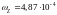 ,
,
Центробежные
моменты инерции
и
оказывают влияние на отклонения по
углам тангажа и курса, причем отклонение
угла тангажа больше ( ,
,
 ).
Из за того что диагональный момент
инерции
).
Из за того что диагональный момент
инерции
 и
и
 больше диагонального момента инерции
больше диагонального момента инерции
 ,
влияние на отклонение по углу тангажа
больше. Отклонение по углу крена
наименьшее (
,
влияние на отклонение по углу тангажа
больше. Отклонение по углу крена
наименьшее ( ,
,
 ,
,
 ),
и начинает увеличиваться только после
3000 секунды, т.к увеличиваются угловые
скорости по другим каналам. Максимальная
угловая скорость
осталась неизменной по сравнению с
расчетом при диагональном тензоре
инерции (
).
Угловые скорости
и
отличны
от полученных при расчете с диагональным
тензором инерции (
),
и начинает увеличиваться только после
3000 секунды, т.к увеличиваются угловые
скорости по другим каналам. Максимальная
угловая скорость
осталась неизменной по сравнению с
расчетом при диагональном тензоре
инерции (
).
Угловые скорости
и
отличны
от полученных при расчете с диагональным
тензором инерции ( ,
, ).
).
При
центробежных моментах инерции
и
отклонения
по углам тангажа, курса меньше чем при
центробежном моменте инерции
( ,
,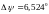 ),
а угловые скорости
),
а угловые скорости
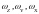 больше (
больше ( ,
,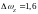 ,
, ).
).
При
центробежных моментах инерции
и
отклонения
по углам тангажа, курса и угловая скорость
меньше чем при центробежном моменте
инерции
( ,
, ,
,
 ),
а угловая скорость
),
а угловая скорость
 и
и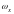 больше
(
больше
( ,
, ).
).
