Прилад виконання завдання

Для балки, схема якої зображена на рис. 5, побудувати епюри Q і М і аналітичним методом визначити необхідний з умови міцності діаметр круглого поперечного перерізу при .

Розв'язання

1. Зображаємо балку з діючими на неї навантаженнями (рис. 5).

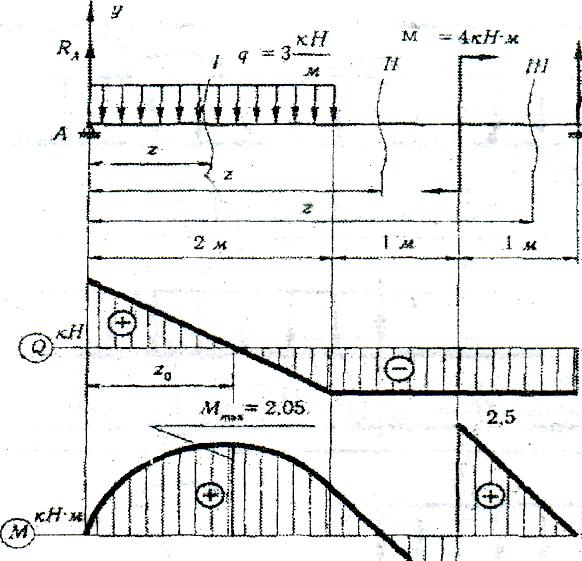
Рис. 5

2. Звільняємо балку від зв'язків і замінюємо їх дію реакціями. Зобра-жуємо розрахункову схему (рис. 5.1).

3. Визначаємо реакції опор з умов рівноваги:

; ,

, ,

Перевірка: ;

Реакції знайдено правильно.

4. Записуємо вирази функцій і для кожної дільниці і знахо-димо значення функцій на границях ділянок.

Балка має три ділянки.

І. ;

- рівняння прямої;

; ;

- рівняння параболи;

; .

ІІ. ;

- рівняння прямої;

- рівняння прямої;

; .

15

ІІІ. ;

- рівняння прямої;

- рівняння прямої;

; .

5. За одержаними даними будуємо епюри, враховуючи характер функцій на кожній ділянці і .

6. В перерізі , де , епюра М має максимум.

Знайдемо абсцису з рівняння ;

.

Знайдемо значення максимального моменту на першій ділянці:

.

7. Підбираємо необхідний з умови міцності діаметр круглого перерізу. Небезпечним є переріз, де виникає найбільший за величиною момент :

,

.

Розмірність: ; .

Приймаємо балку діаметром d=54 мм.

Питання для самоперевірки

1. Що називається балкою?

2. Який згин називається прямим, косим, чистим?

3. Сформулюйте правила знаків для поперечних сил і згинаючих моментів?

4. Чому дорівнює поперечна сила в будь - якому поперечному перерізі балки?

5. Чому дорівнює згинаючий момент в будь - якому поперечному перерізі балки?

6. Що називають епюром і для чого їх будують?

7. Скільки і які методи застосовують для побудови епюр при деформації згину?

8. Записати умову міцності при деформації згину.

9. Як визначити найбільший допустимий згинаючий момент?

10. Що називають осьовим моментом опору?

Практичне заняття № 5 Розрахунок валів на сумісний згин з крученням

Мета: Виробити уміння і навички побудови епюр обертових та згинаючих моментів. Навчитись проводити розрахунки валів на міцність при сумісному згині з крученням.

16

Література: Л. 1 с. 321 – 234; Л. 3 с. 112 – 118; Л. 4 с. 201 – 203.

Теоретичні відомості

Складний деформований стан виникає в тих випадках, коли елемент конструкції або машина піддається декільком найпростішим навантаженням. Прикладом складного деформування є вали, які працюють на згин з кручен-ням. При цьому в поперечному перерізі вала виникають нормальні та дотичні напруження. Нормальні напруження, які виникають від згину, досягають максимального значення в волокнах, найбільш віддалених від нейтральної вісі:

,

де - згинаючий момент; - осьовий момент опору перерізу.

Максимальні дотичні напруження при крученні виникають в точках контуру поперечного перерізу:

,

де - полярний момент опору.

Оскільки

,

то .

У випадку сумісної дії М_об і М_зг у небезпечній точці перерізу діють, як правило, нормальне і дотичне напруження. Тому під час розрахунків валів на сумісний згин з крученням необхідно встановити, яке з цих напру-жень або яка їх комбінація визначає міцність вала. Відповідь на це питання дають так звані теорії (гіпотези) міцності, згідно з якими небезпечний стан виникає:

• при досягненні нормальними напруженнями межі міцності або теку-чості;

• коли найбільше відносне видовження досягає певного значення;

• дотичні напруження досягають певного значення;

• значення енергії, яка накопичується в матеріалі при деформації, досягає певного значення.

В залежності від прийнятої гіпотези міцності визначають еквівалентне напруження , яке можна порівняти з напруженням при осьовому навантаженні. У відповідності до умов міцності еквівалентне напруження не повинно перевищувати допустиме напруження для матеріалу.

Умова міцності при сумісній дії згину з крученням має вигляд:

;

;

17