Прилад виконання завдання

До точки прикладені О сили: , , , які лежать в одній площині і утворюють з віссю х кути: , , . Визна-чити величину і напрям рівнодіючої даної системи сил.

Вказівки до розв'язку. Напрям рівнодіючої можна визначити одним кутом; який відлічують від позитивного напряму осі х проти годинникової стрілки до напряму рівнодіючої. Кут знаходиться в межах від до і визначається як кут між віссю х і рівнодіючою.

Розв'язок

1. Аналітичний спосіб.

1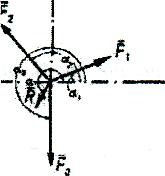 .1. Проводимо координатні осі та відкладаємо в даній системі координат сили під заданими кутами (рис. 1).

1.2. Визначаємо проекції рівнодіючої на координатні осі як суму проекцій заданих сил на ці осі:

.

Рис. 1

6

.

Визначаємо модуль рівнодіючої:

.

1. 3. Визначаємо кут між напрямом і віссю х:

; .

Оскільки косинус і синус кута від'ємні, то кут повинен розміщува-тись у третій чверті. Знаходимо кут . Відлічуємо цей кут від осі х проти руху годинникової стрілки і проводимо рівнодіючу .

Графічний спосіб

2.1. Вибираємо масштаб сил . Визначаємо довжини сторін силового багатокутника, які відповідають в масштабі заданим силам:

, , .

2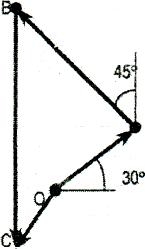 .2. З довільної точки О проводимо відрізок , рівний вектору заданої сили (рис. 2). З кінця А цього відрізка проводимо відрізок . З кінця В цього відрізка проводимо відрізок . Замикаюча сторона отриманого силового багатокутника відповідає рівнодіючій заданої сис-

теми сил у вибраному масштабі: , отже, Рис. 2

модуль рівнодіючої дорівнює:

.

Вимірюємо кут між горизонталлю і замикаючою стороною .

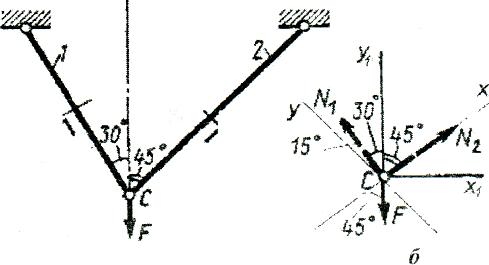
Приклад визначення реакцій стержня

Система двох стержнів навантажена силою (рис.3, а). Визначити реакції стержнів, Масою стержнів знехтувати.

Розв 'язок

1. Розглядаємо рівновагу шарніра С, на якій діє система збіжних сил: активна сила та реакції зв'язків N₁ та N₂ (рис. 3, а).

а) б)

Рис.3

7

2. Вибираємо систему координат , провівши вісь х через невідому реакцію N₂.

3. Складаємо рівняння (рис. 3, б):

,

4. Визначаємо зусилля в стержнях:

,

.

5. Виконуємо перевірку, вибравши нове розміщення координатних осей х₁Су₁ (рис. 3,б)

,

отже, зусилля в стержнях визначено правильно.

Відповідь: , .

Питання для самоперевірки

1. Що називають механічним рухом?

2. Що називають системою?

3. Що називають силою, чим вона характеризується та в яких одиницях вона вимірюється?

4. Що називають матеріальною точкою, абсолютно твердим тілом??

5. Які сили називають збіжними?

6. Сформулюйте аксіоми статики.

7. Що називають в'яззю, силою реакції в'язі?

8. Що називається проекцією сили на вісь?

9. Чому дорівнює проекція сили на вісь?

10. Які рівняння рівноваги можна скласти для плоскої системи збіжних сил?

Практичне заняття № 2 Рівновага плоскої системи довільно розміщених сил

Мета: Закріпити теоретичні знання при вивченні методики розв'язку задач. Набути навичок виконання розрахунково - графічної роботи по визна-ченню реакцій опор заданої двохопорної балки.

Література: Л. 1 с. 34 – 45; Л. 3 с. 27 – 41; Л. 4 с. 29 – 33.