Метод Рунге — Кутта второго порядка

Рассмотрим метод Рунге — Кутта второго порядка (метод Эйлера — Коши).

В этом методе величины у_i+1 вычисляются по следующим формулам (рис. 7):

y_i+1 = y_i+ y_i; y_i = y_i1 + y_i2,

y_i1 = f(x_i, y_i), y_i2 = f(x_i + h, y_i + hf(x_i, y_i).

Тогда

y_i+1 = y_i + h

Обозначим

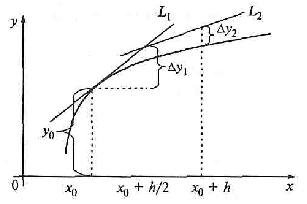
Рис. 7. Метод Эйлера — Коши

тогда

y_i+1 = y₁ + h

Геометрически это означает, что определяется направление интегральной кривой в исходной точке (х_i у_i) и во вспомогатель­ной точке (х_i+1, у*_i+1), а в качестве окончательного выберем сред­нее из этих направлений.

Пример 4. Решить методом Эйлера дифференциальное уравнение y'=cosy+3x методом Рунге — Кутта второго по­рядка (начальное условие у(0)= 1,3 на отрезке [0; 1]).

Программа_____________________________________________________

Program Rumge; {Метод Рунге — Кутта 2-го порядка}

Uses Crt;

var z,x,y,a,b,h:real;

function f(x,y:real):real;

begin

f:= cos(y)+3*x;

end;

begin

ClrScr;

writeln('Введите у, a, b, h'); readln(y,a,b,h); x:=a;

repeat

writeln(x:0:3,' *,y:0:3); z:=y+h*y*(l-x);

y:=y+h*(f(x,y)+f(x+h,z))/2; x:=x+h;

until x>b+0.1;

readkey;

end.

Метод Рунге — Кутта 4-го порядка

В вычислительной практике наиболее часто используется ме­тод Рунге — Кутта четвертого порядка. В этом методе величины у_м вычисляются по следующим формулам:

y_i+1 = y_i+ y_i;

y_i = h(k₁ + 2k₂ +2k₃ + k₄)/6, где i = 0,1,…;

k₁ =f(x_i, y_i);

k₂ = f(x_i + h/2, y_i +hk₁/2);

k₃ = f(x_i + h/2, y_i +hk₂/2);

k₄ = f(x_i + h, y_i +hk₃);

Пример 5. Пусть дано дифференциальное уравнение у' = у - х с начальным условием у(0) =1,5.

Найти с точностью = 0,01 решение этого уравнения мето­дом Рунге — Кутта при х= 1,5.

Решение

Пусть h = 0,25.

Весь отрезок интегрирования [0; 1,5] разобьем на шесть час­тей точками:

х₀ = 0, х₄ = 1;

x₁ = 0,25; х₅ = 1,25;

х₂ = 0,5; х₆=1,5.

х₃ = 0,75;

Из начальных условий имеем х₀ = 0; у₀ = 1,5.

Найдем первое приближение

y₁ = y₀+ y₀, где y₀ = (k₁ +2k₂ +2k₃ + k₄).

Используя формулы метода Рунге — Кутта, получаем

k₁ =(y₀ – x₀)h = 1,5 * 0,25 = 0,375;

k₂ = [(y₀ + ) – (x₀ + )]h = [(1,5 + 0,187) – 0,125] * 0,25 = 0,39;

k₃ = [(y₀ + ) – (x₀ + )]h = 0,392;

k₄ = [(y₀ +k₃) – (x₀ +h)]h = 0,41.

Следовательно

y₀ = (0,375 + 2 * 0,39 + 2 * 0,392 + 0,41) = 0,392.

Отсюда

y₁ = 1,5 + 0,392 =1,892 и т. д.

Пример 6. Проинтегрировать дифференциальное уравне­ние

методом Рунге — Кутта на отрезке [0; 2] и выдать на печать зна­чение функции в каждой двадцатой точке. В качестве шага ин­тегрирования можно взять h= 0,005, в качестве начальных усло­вий — у(0) = 1.

Программа_____________________________________________________

F(X,Y) — подпрограмма-функция (правая часть уравнения)

Program Dif;

Uses Crt;

Const H= 0.005;

Var X,Y:Real;

Fl,F2,F3,F4:real;

I,N:lnteger;

Begin

ClrScr;

X:=0; Y:=l; N:=20;

Forl:=l TON DO

Begin X:=X+H;

F1:=H*F(X,Y);

F2:=H*F(X+H/2.,Y+Fl/2.);

F3:=H*F(X+H/2.,Y+F2/2.);

F4:=H*F(X+H,Y+F3);

Y:=Y+( F1 +2* F2+2* F3+F4)/6;

End;

Writeln('Y=' Y:8:3)

Readkey;

End.

Замечание. Метод Рунге—Кутта для решения дифференциального уравнения вида

сводится к последовательному вычислению следующих равенств

x_i+1 = x_i+h;

k₁ =hF(x_i, y_i);

k₂ = hF(x_i + h/2, y_i +hk₁/2);

k₃ = hF(x_i + h/2, y_i +hk₂/2);

k₄ = hF(x_i + h, y_i +hk₃);

y_i+1 =y_i +1/6(k₁ + 2k₂ +2k₃ + k₄), где i = 1,…n.

Пример 7. Решить дифференциальное уравнение

у(0) = 1,3 на отрезке [0; 1] методом Рунге — Кутта 4-го порядка.

Программа________________________________________________

Program Runge; {Метод Рунге - Кутта 4-го порядка}

var kl ,k2,k3,k4,x,y,a,b,h,d:real;

function f(x,y:real):real;

begin

f:= cos(y)+3*x;

end;

begin

writeln('Введите у, a, b, h'); readln(y,a,b,h);

x:=a;

repeat

writeln(x:0:3,' ',y:0:3);

kl:=f(x,y);

k2:=f(x+h/2,y+h*kl/2);

k3:=f(x+h/2,y+h*k2/2);

k4:=f(x+h,y+h*k3);

d:=(kl+2*k2+2*k3+k4)/6;

y:=y+d; x:—x+h;

until x>b+0.1;

readln;

end.