Сравнение выборочной дисперсии предполагаемым значением.

Для с.в. Х получена выборка, по которой найдена точная оценка для дисперсии S_x².

Гипотезу проверяем по критерию Х².

(16)

Х²

f(x)

(Х²_кр)^лев n-1 (Х²_кр)^пр x

Различные варианты альтернативной гипотезы:

1. 

0

1. по выборке Х²_набл (ф-ла 16)

2. по таблицам Х²_кр(α;k). K=n-1;

3. Х²_набл>Х²_кр M₀ отвергаем

Х²_набл<Х²_кр M₀ принимаем

1. 

0 (Х²_кр)^лев (Х²_кр)^пр

1. по выборке Х²_набл (ф-ла 16);

2. по таблицам 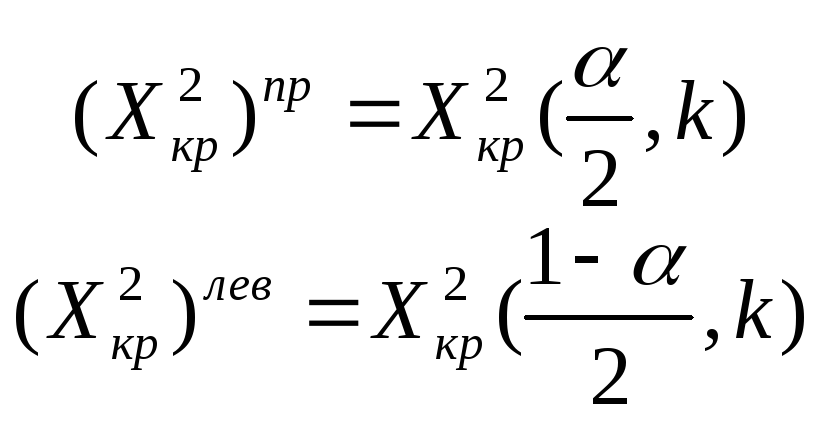k=n-1

3. (Х²_кр)^лев<Х²_набл<(Х²_кр)^пр M₀ принимаем

Х²_набл< (Х²_кр)^лев <(Х²_кр)^пр M₀ отвергаем

Проверка гипотезы о равенстве дисперсий нескольких нормальных распределений.

Критерий Коглена ( выборки одинакового объема): для нескольких с.в. х₁, х₂…х _е получены выборки одинакового объема n. Для каждого найдены S²₁, S²₂…S²_e. Проверяется гипотеза об однородности дисперсии M₀: D₁=D₂=…D_e.

(17)

Порядок проверки:

1. по выборке G_набл (ф-ла 17);

2. по таблицам крит. Точек распред-ия Когрена G_кр (α, k, l)

3. G_набл>G_кр M₀отвергается;

G_набл<G_кр M₀принимается.

Cравнение нескольких дисперсий нормальных распределений для выборок различного объема

Критерий Бартлета: для нес. С.в. х₁, х₂…х_lполучены выборки с разл.V n₁, n₂…n _l . По ним найдены оценки дисперсииS²₁,S²₂…S²_l.

M₀: D₁=D₂=…D_e.

(18)

k_i=n_i–1 – числа степеней свободы

k=

- средневзвешенная всех исправленных дисперсий

Если Vвсех выборокn_i≥4, то с.в. В приблизительно подчиняется распр-ю Х²с числом степеней свободыl-1.

Порядок проверки:

1. по выборкам В_набл(ф-ла 18)

2. по таблицам крит. точек распред-ия Х² Х² кр (α, k, l-1)

3. В_набл> Х²кр гипотеза отвергается;

В_набл< Х²кр гипотеза принимается

Критерии согласия

Критерии согласия наз-ся критерий для проверки гипотезы о виде з/п-на распределения. Критерии Пирсона, Ромнаовского, Колмогорова.

1. Критерий Пирсона

При построении з-на распределения по опытным данным варианты группируются по повторяемости (для дискретных с.в.) или по-интервально (для непрерывных с.в.). При проверке гипотезы о виде з/п-на распред-я по ф-лам предполагаемого з-на подсчитываются вер-ти р_i попаданий в полученные группы. Имея вер-ти подсчитываем теоретические частотыпопаданий в эти группы.

= р_in

Экспериментальные частоты сравниваются с теоретическими по критерию Пирсона.

Критерий Пирсона приблизительно имеет распр-ние Х²(приn>10). По таблицам находимX²_кр(α,к), где α – уровень зависимости, к – число степеней свободы.

, где S– число групп , κ – число параметров распределения, оцениваемых по выборке.

Замечания:если при группировке появляются малочисленные группы, то их надо объединять с соседними группами. В этом случаеS– число объединенных групп.

Например:

xi	0	1	2	3	4	5
ni	75	41	12	4	2	1
	83.5	54.2	8.3	3.1	1.5	0.7

X²_набл<X²_крM₀принимаем

X²_набл>X²_крM₀отвергаем.

1. Критерий Колмагорова.

Сравнивается эмпирическая функция распределения F^*(x), построенная по выборке и теоретическаяF(x), построенная по формулам предполагаемого закона. Если различия между ними значимо, то гипотеза отвергается , незначимо – принимается. Мерой отклонения этих функций служит разница их значения в экспериментальных точкахx_i.

F^*(x)

F(X)

1

x₁ x₂ x₃ x₄

Для каждой x_i записывается значение предела справа и предела слева F^*(x-0),F^*(x+0).

Подсчитываем теоретическую функцию F(x) и выбираем большую из разностей между ними Δi:

xi	F*(x-0)	F*(x+0)	F(x)	Δi
2.3	0	1/n=0.1	0.05	0.05
3.7	1/n=0.1	2/n=0.2	025	015

n=10

Среди всех Δi выбираем максимум и сравниваем с критическим значением ε(α,n), которые находятся по таблице критических точек распределения Колмагорова.

Δi_max< ε(α,n) M₀ принимаем;

Δi_max> ε(α,n) M₀ отвергаем.

Замечание: в критерий Колмагорова параметры распределения предполагаются уже известными, они не оцениваются по выборке.