4.6.3. Задание точек методом «направление – расстояние»

Вместо ввода координат допускается использовать прямую запись paccmояния, что особенно удобно для быстрого ввода длины линии. Такой ввод может быть использован во всех командах, кроме тех, в которых необходимо вводить действительное значение.

При использовании прямой записи расстояния на запрос точки достаточно переместить устройство указания в нужном направлении и ввести числовое значение в командной строке. Например, если таким способом задается отрезок, то он строится заданием числового значения длины и направления под определенным углом. При включенном орто-режиме этим способом очень удобно рисовать перпендикулярные отрезки.

4.6.4. Задание трехмерных координат

Трехмерные координаты задаются аналогично двумерным, но к двум составляющим по осям Х и Y добавляется третья координата по оси Z. В трехмерном пространстве аналогично двумерному моделированию можно использовать абсолютные и относительные координаты, а также цилиндрические и сферические координаты, которые схожи с полярными координатами в двумерном пространстве.

Значения координат независимо от способа ввода всегда связаны с некоторой системой координат. При работе в трехмерном пространстве значения координат x, y и z указываются либо в мировой системе координат, либо в пользовательской системе координат.

4.6.5. Правило правой руки

При работе в трехмерном пространстве все системы координат формируются по правилу правой руки. Это правило определяет положительное направление оси Z трехмерной системы координат при известных направлениях осей X и Y, а также положительное направление вращения вокруг любой из осей трехмерных координат.

Д

Рис. 4.2

ля определения положительных направлений осей необходимо поднести тыльную сторону кисти правой руки к экрану монитора, направить большой палец следует параллельно оси X, а указательный – по оси Y. Если согнуть средний перпендикулярно ладони, как показано на рис. 4.2 справа, то он будет указывать положительное направление оси Z.

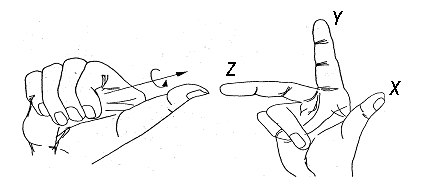
Для определения положительного направления вращения следует ориентировать большой палец правой руки в положительном направлении оси и согнуть остальные пальцы, как показано на рис. 4.2. слева. Положительное направление вращения будет совпадать с направлением, указываемым согнутыми пальцами.

4.6.6. Ввод трехмерных декартовых координат

Трехмерные декартовы координаты (x,y,z) вводятся аналогично двумерным координатам (x,y). Дополнительно к указанию координат по осям X и Y необходимо ввести еще и координату по оси Z. На самом деле в компьютерной графике не существует двумерных координат, и если введены значения только x и y, это означает, что отсутствующая координата z по умолчанию равна нулю. Ввод декартовых трехмерных координат с клавиатуры представляет собой ввод трех чисел через запятую.

Например: 3,5,2.

В трехмерном пространстве, так же как и в двумерном, широко используются абсолютные координаты (отсчитываемые от начала координат), и относительные (отсчитываемые от последней указанной точки). Признаком относительных координат является символ @ перед координатами вводимой точки. В этом случае вводимая точка берется относительно последней введенной точки.