Пример выполнения задания 4 а)

Условие. Найти производную сложной функции .

Решение.

1. Найдем частные производные, входящие в формулу

. (3.1)

;

;

; .

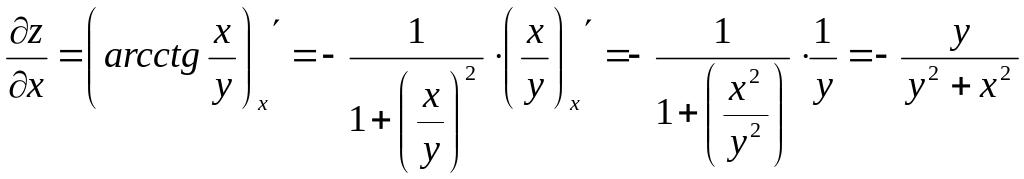2. Используя формулу (3.1), получим:

.

ОТВЕТ .

Пример выполнения задания 4 б)

Условие. Найти частные производные и функции .

Решение.

1. Найдем все частные производные, входящие в формулы (3.3)

и ;

;

;

;

; .

2) В соответствии с формулами (3.3) получим:

;

+

.

ОТВЕТ. ,

.

Пример выполнения задания 5 а)

Условие. Показать, что функция удовлетворяет уравнению .

Решение.

1. Упростим заданную функцию

.

2. Найдем все частные производные, входящие в уравнение.

= ;

= .

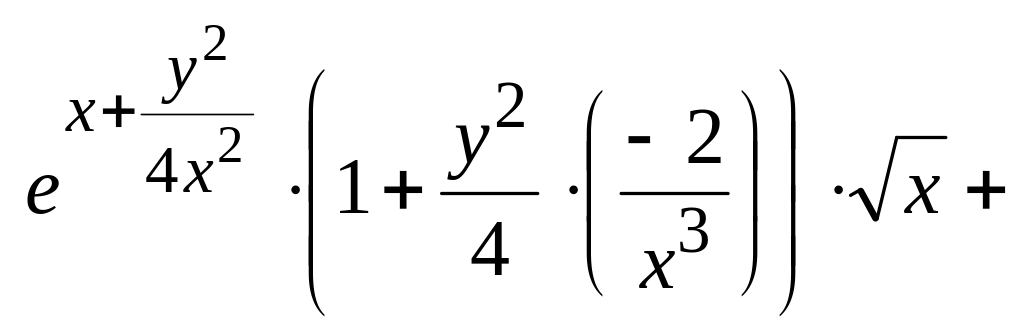
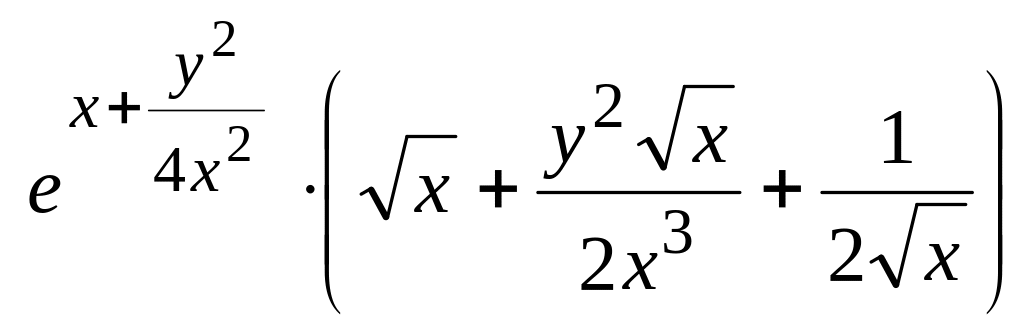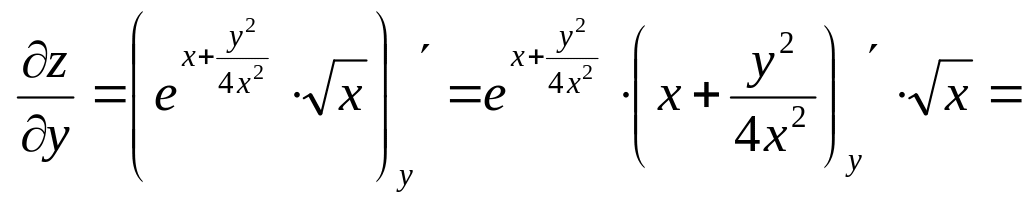
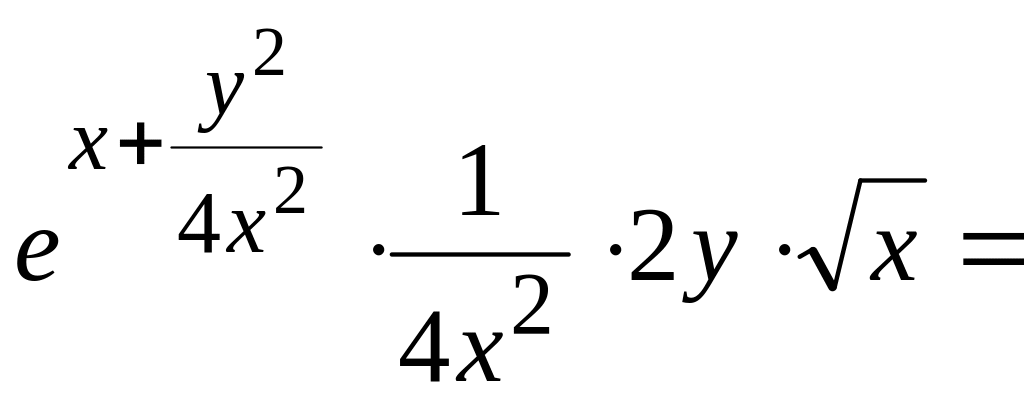
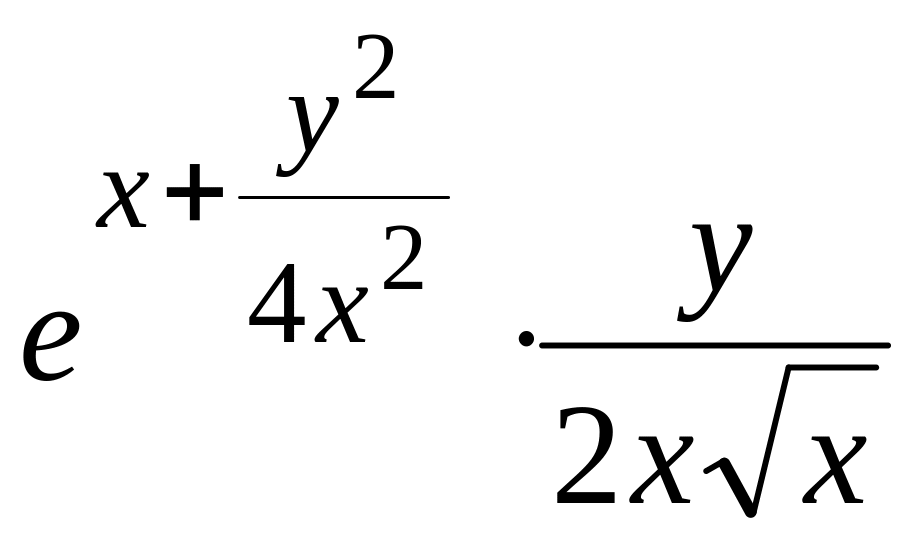3. Подставим найденные производные в исходное уравнение:

=

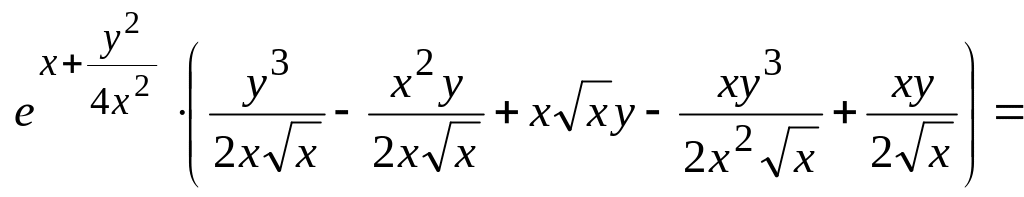
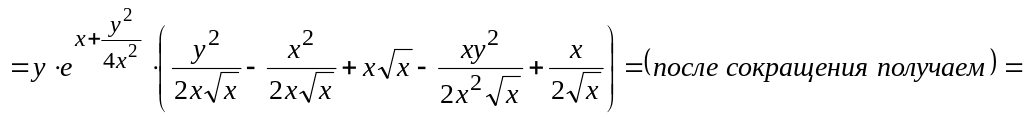
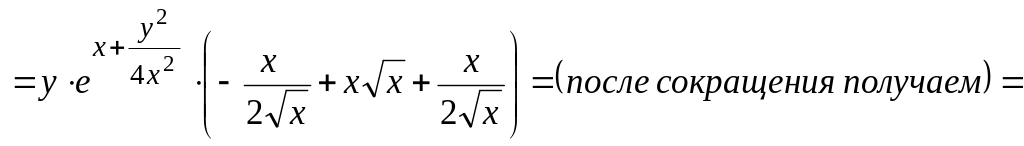
= , что и требовалось показать.

Пример выполнения задания 5 б)

Условие. Показать, что функция удовлетворяет

уравнению .

Решение.

1. Найдем все частные производные, входящие в уравнение.

;

; .

2. Подставим найденные производные в исходное уравнение

.

=

=

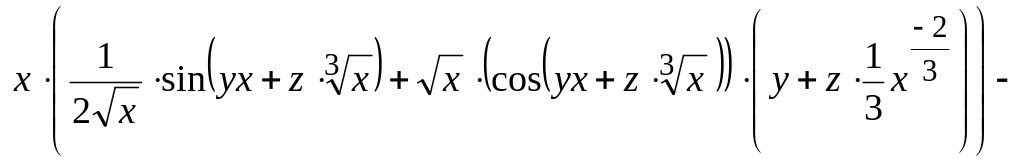
, что и требовалось показать.

Пример выполнения задания 6 а)

Условие. Найти производную неявной функции , заданной уравнением .

Решение.

1. Здесь =0.

2. Производную неявной функции , заданной с помощью уравнения , можно найти по формуле

, при условии (3.4),

где – дифференцируемая функция переменных и .

Найдем частные производные

.

3. По формуле (3.4) получаем .

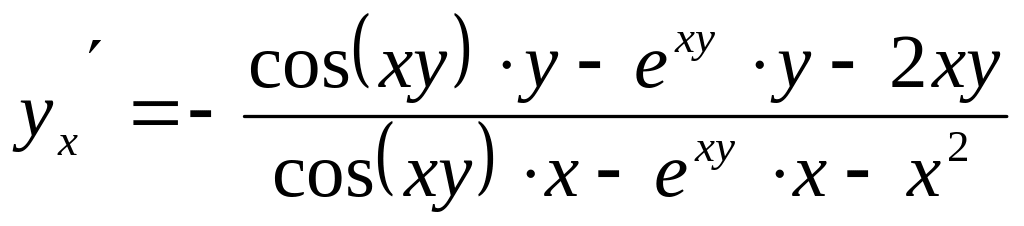ОТВЕТ. .

Пример выполнения задания 6 б)

Условие. Найти частные производные и неявной функции , заданной уравнением .

Решение.

1. Здесь .

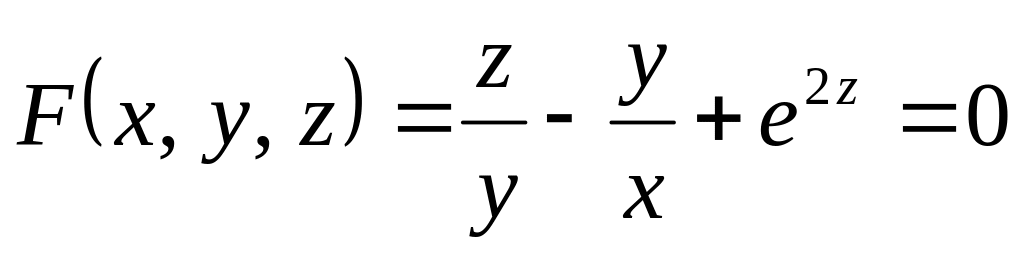2. Частные производные неявной функции двух переменных , заданной уравнением 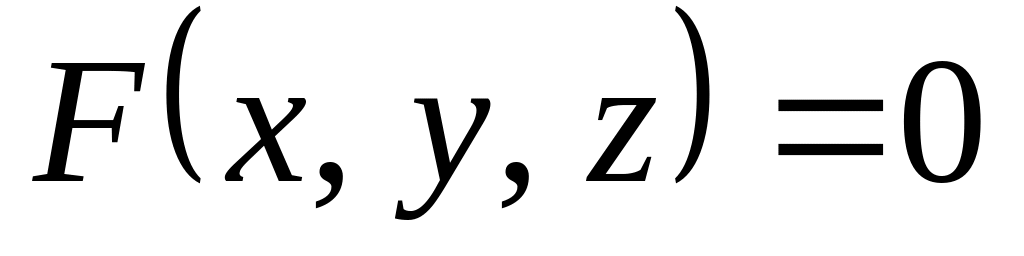, вычисляются по формулам:

, , при условии, что (3.5)

3. Найдем частные производные функции

;

;

.

4. Частные производные неявной функции двух переменных , определяются следующим образом:

;

= .

ОТВЕТ. , .

Пример выполнения задания 7 а)

Условие. Найти производную функции в точке в направлении вектора и градиент функции в этой точке.

Решение.

1. Производная в направлении вектора 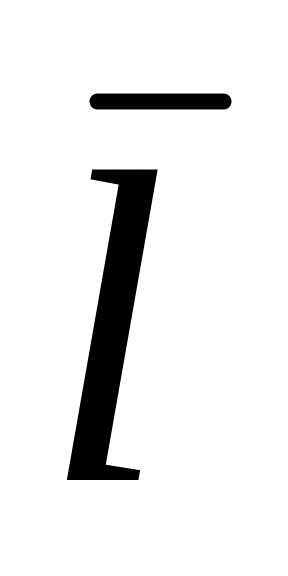определяется по формуле

(5.2)

где , – направляющие косинусы вектора .

2. Найдем частные производные заданной функции и вычислим их значения в точке :

, , при условии .

Получим ;

.

3. Тогда частные производные неявной функции двух переменных , определяются следующим образом:

; .

4. Вычислим значения частных производных в точке :

; .

5. Найдем длину вектора и его направляющие косинусы:

;

; .

6. Используя формулу (5.2), получим производную функции z в направлении вектора :

.

7. По формуле (5.3) имеем: .

ОТВЕТ. , .