
- •Функции нескольких переменных
- •Содержание
- •Введение
- •§ 1. Понятие функции двух переменных
- •§ 2. Частные производные и дифференциалы функции нескольких переменных
- •§ 3. Производная сложной и неявной функции
- •§ 4. Касательная плоскость и нормаль к поверхности
- •§ 5. Производная по направлению. Градиент. Линеаризация
- •§ 6. Частные производные и дифференциалы высших порядков
- •§ 7. Экстремум функции двух переменных
- •§ 8. Наибольшее и наименьшее значение функции нескольких переменных в замкнутой области
- •Задания для самостоятельной работы студентов
- •Пример выполнения заданий самостоятельной работы студентов Пример выполнения задания 1 а)
- •Заданная функция двух переменных определена, если подкоренное выражение в каждом слагаемом неотрицательно, т.Е. Выполняется система двух неравенств: .
- •Пример выполнения задания 1 б)
- •Пример выполнения задания 2 а)
- •Пример выполнения задания 2 б)
- •Найдем частные производные первого порядка заданной функции трех
- •Пример выполнения задания 3
- •Пример выполнения задания 4 а)
- •Пример выполнения задания 4 б)
- •Пример выполнения задания 5 а)
- •Пример выполнения задания 5 б)
- •Пример выполнения задания 6 а)
- •Пример выполнения задания 6 б)
- •Пример выполнения задания 7 а)
- •Пример выполнения задания 7 б)
- •Пример выполнения задания 8
- •Пример выполнения задания 9
- •Пример выполнения задания 10
- •Литература
§ 7. Экстремум функции двух переменных
Точка
![]() называется точкой
максимума
функции
,
если существует такая
называется точкой
максимума
функции
,
если существует такая
![]() -
окрестность точки
-
окрестность точки
![]() ,
что для каждой точки
,
отличной от точки
из этой окрестности, выполняется
неравенство
,
что для каждой точки
,
отличной от точки
из этой окрестности, выполняется
неравенство
![]() .
.
Точка
называется точкой
минимума
функции
,
если существует такая
-
окрестность точки
,
что для каждой точки
,
отличной от точки
из этой окрестности, выполняется
неравенство
![]() .
.
Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимум и минимум функции называются ее экстремумами.
Если дифференцируемая функция имеет экстремум в точке , то ее частные производные в этой точке равны нулю, т.е.
![]() и
и
![]() .
.
Точки, в которых частные производные первого порядка функции равны нулю, называются стационарными.
Пусть в стационарной точке и некоторой ее окрестности функция имеет непрерывные частные производные до второго порядка включительно. Вычислим значения частных производных второго порядка в этой точке
![]() ,
,
![]() ,
,
![]() .
.
Обозначим
через
![]() .
Тогда:
.
Тогда:
если
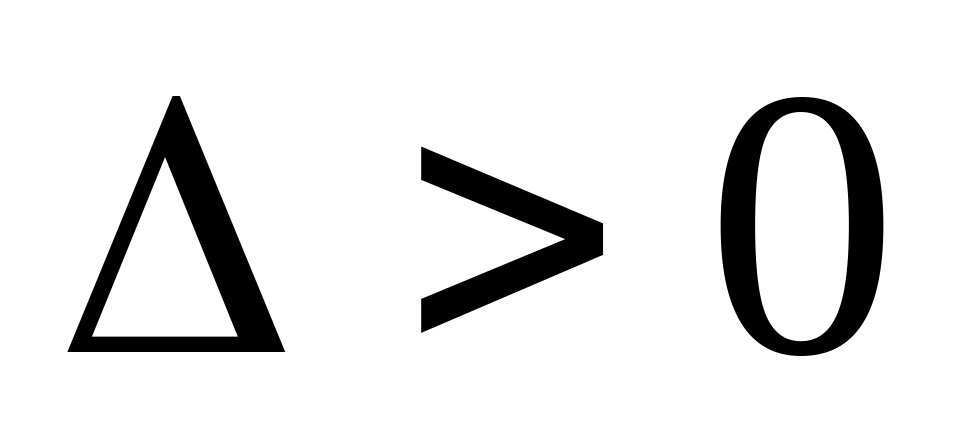 ,
то функция
имеет в точке
экстремум, а именно, максимум при
,
то функция
имеет в точке
экстремум, а именно, максимум при
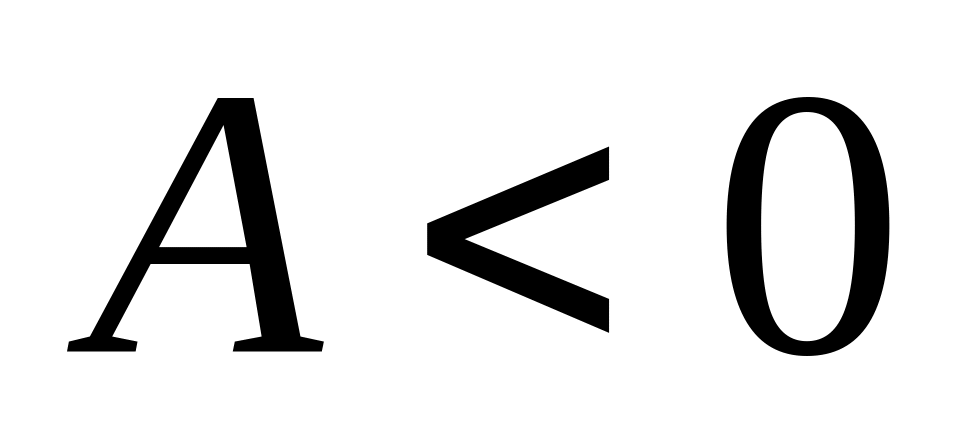 и минимум при
и минимум при
 ;
;если
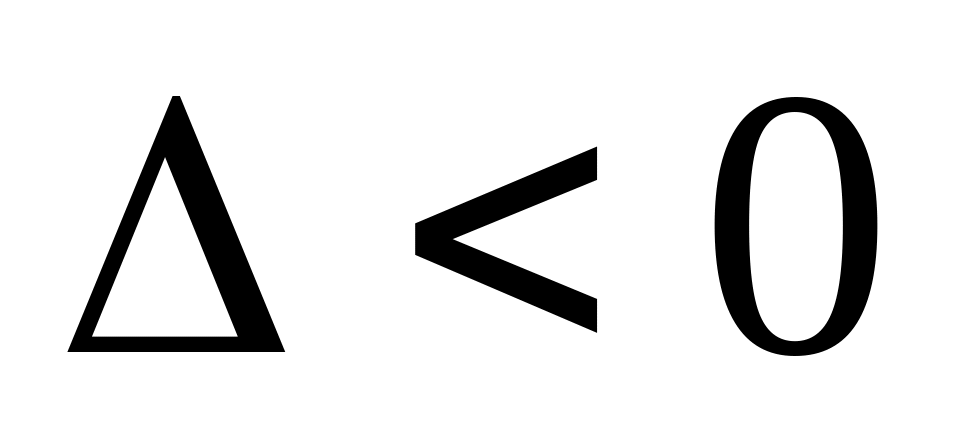 ,
то в этой точке экстремума нет;
,
то в этой точке экстремума нет;если
 ,
то необходимы дополнительные исследования.
,
то необходимы дополнительные исследования.
§ 8. Наибольшее и наименьшее значение функции нескольких переменных в замкнутой области
Пусть функция определена и непрерывна в ограниченной замкнутой области . Тогда она достигает в некоторой точке этой области своего наибольшего и наименьшего значений. Эти значения достигаются функцией в точках, расположенных внутри области , или в точках, лежащих на границе области.
Для того чтобы найти наибольшее и наименьшее значения функции в замкнутой области, надо:
1) найти стационарные точки, расположенные в данной области, и вычислить значения функции в этих точках;
2) найти наибольшее и наименьшее значения функции на линиях, образующих границу области;
3) из всех найденных значений выбрать наибольшее и наименьшее.
Задания для самостоятельной работы студентов
Задание№1.
Н![]() айти
и изобразить область определения функции
нескольких переменных.
айти
и изобразить область определения функции
нескольких переменных.
а)
 б)
б) 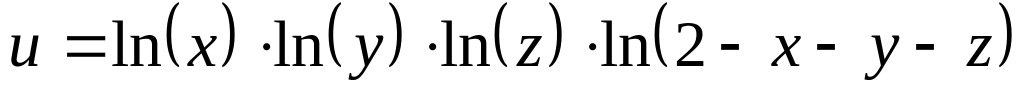
а)
 б)
б) 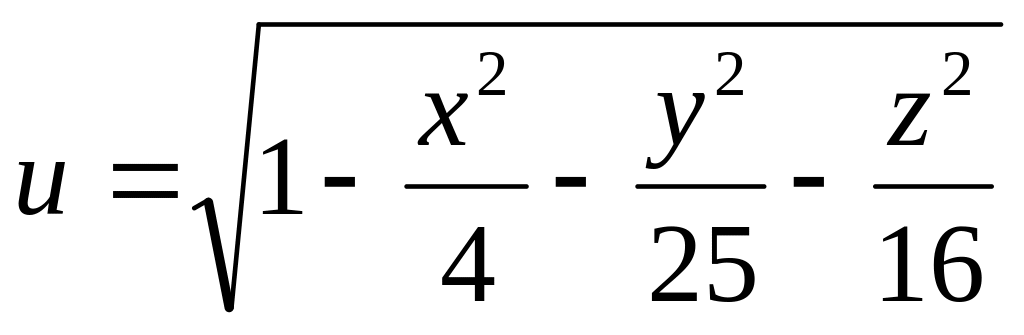
а)
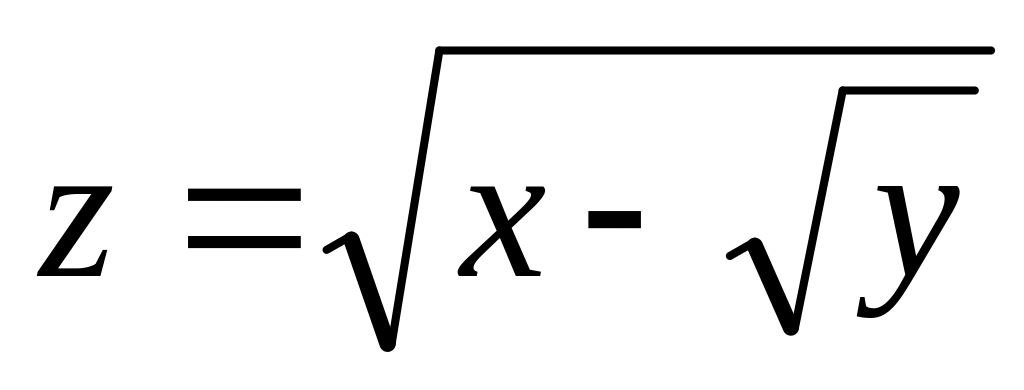 б)
б) 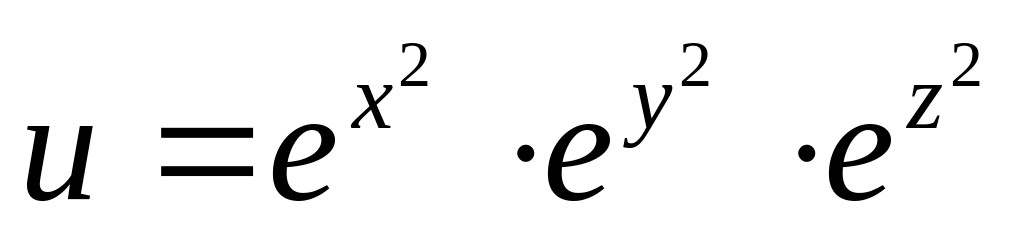
а)
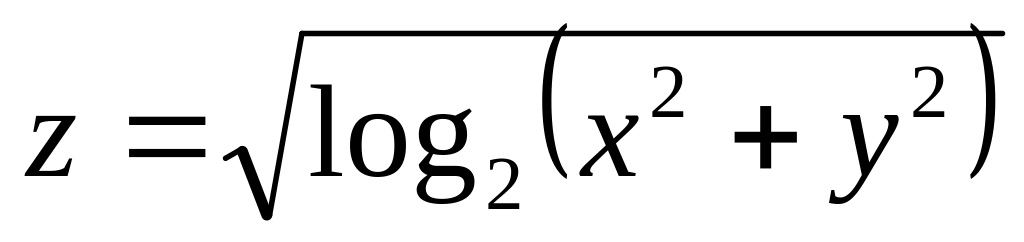 б)
б) 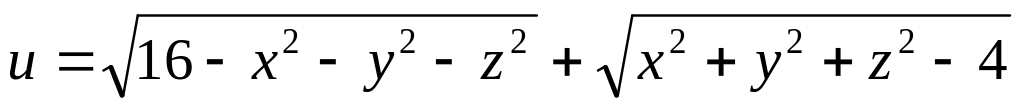
а)
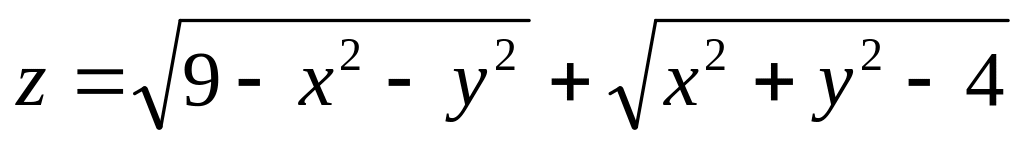 б)
б) 
а)
 б)
б) 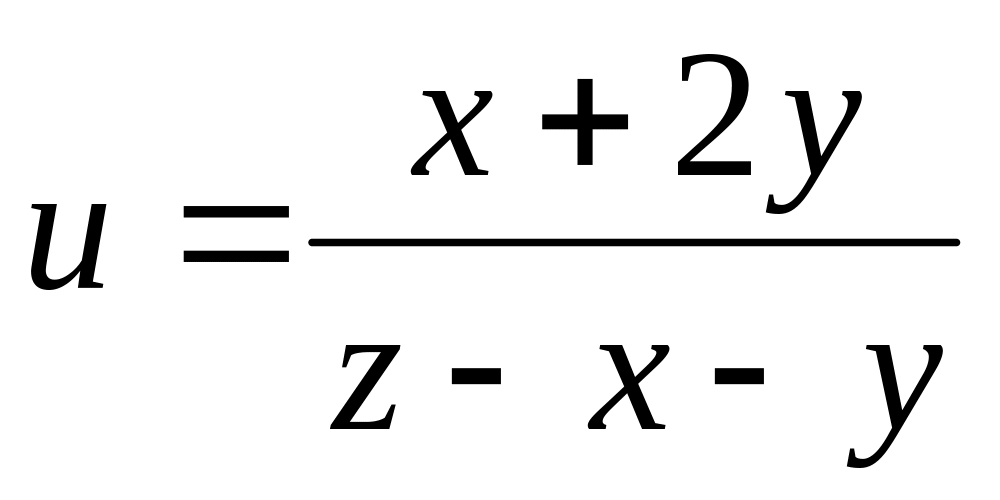
а)
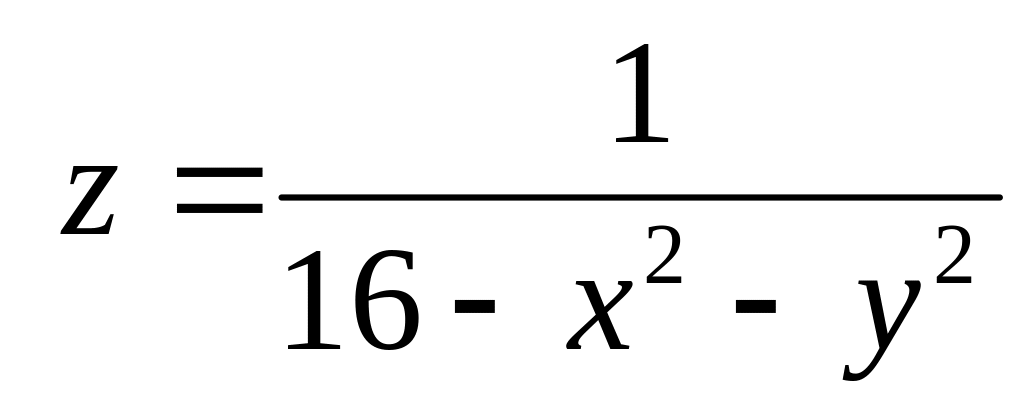 б)
б) 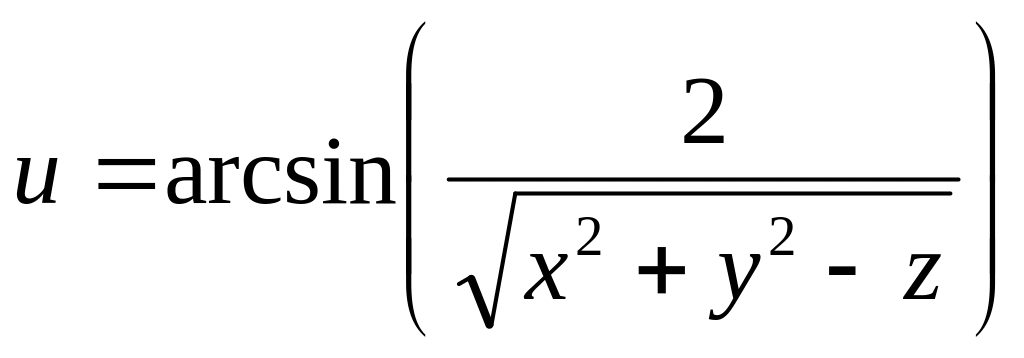
а)
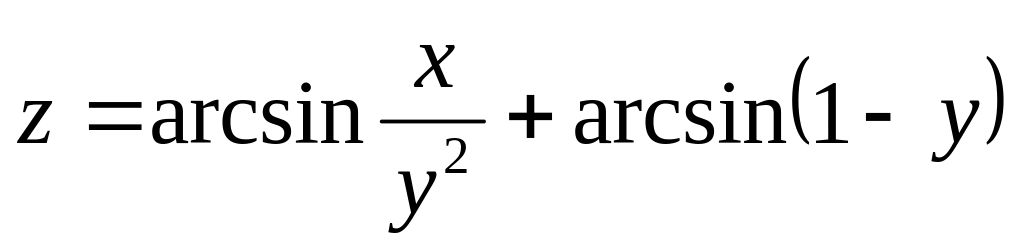 б)
б) 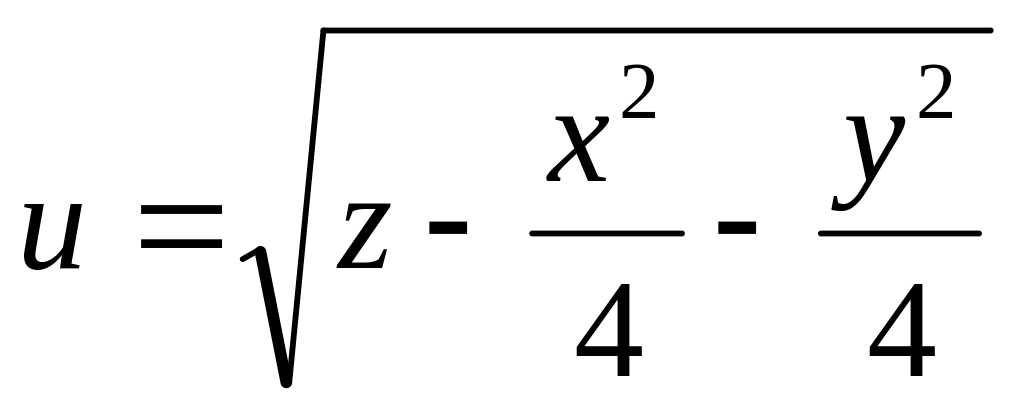
а)
 б)
б) 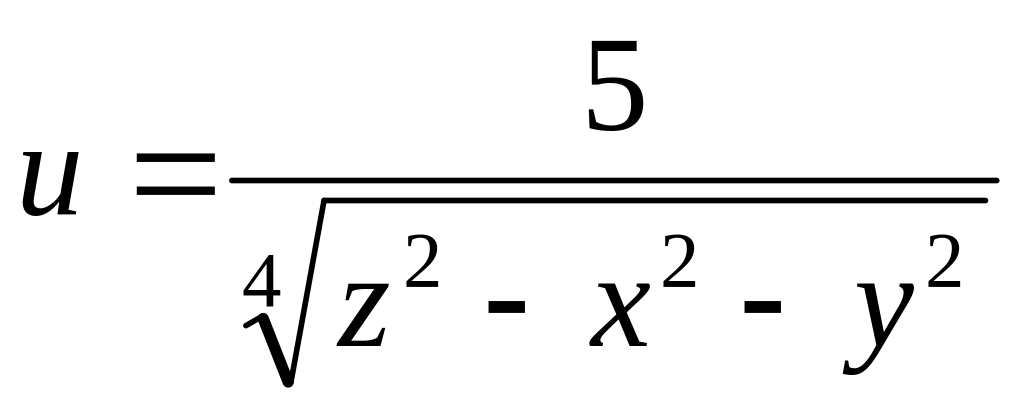
а)
 б)
б) 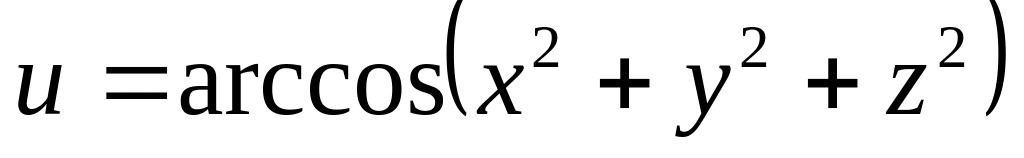
а)
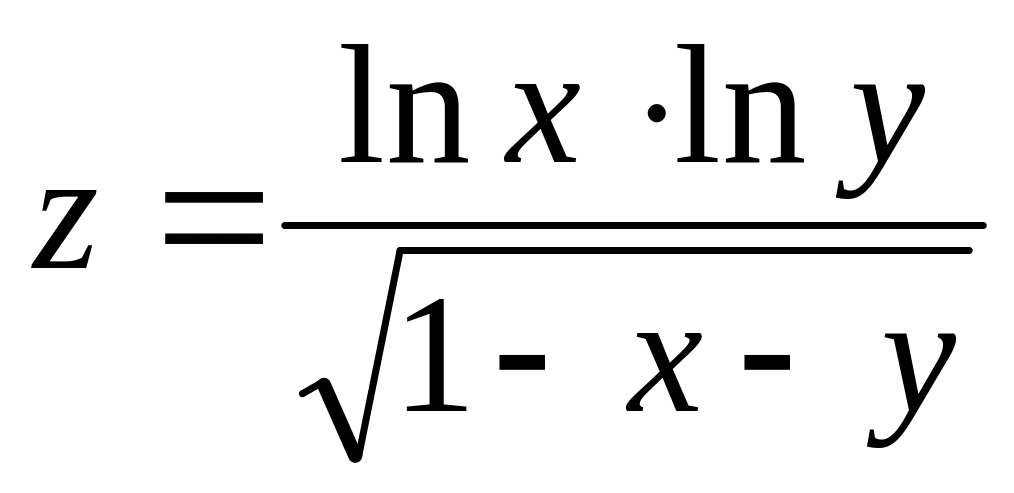 б)
б) 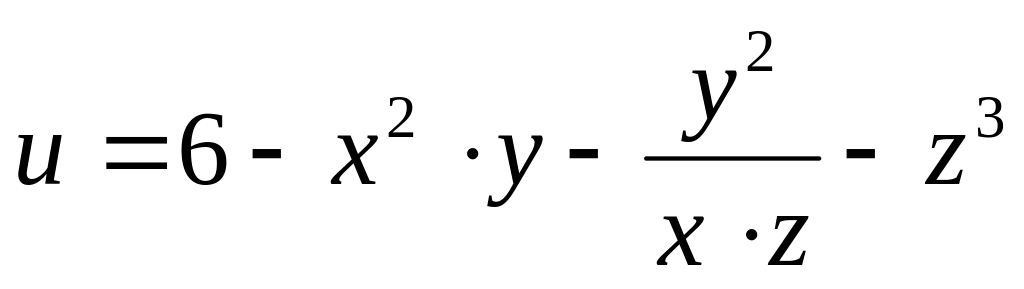
а)
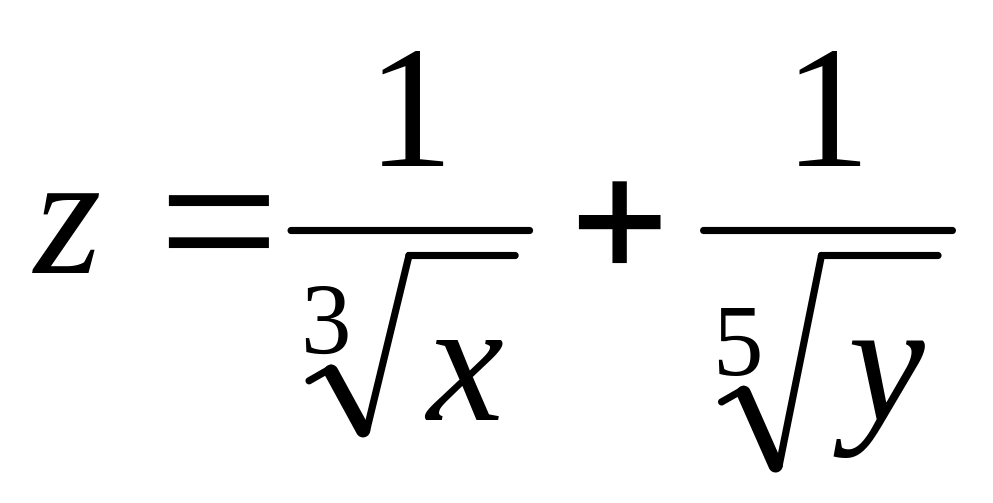 б)
б) 
а)
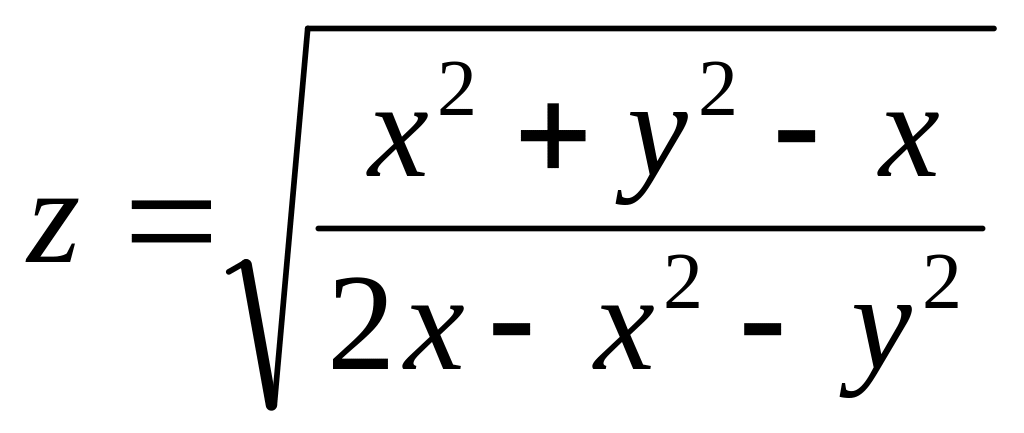 б)
б) 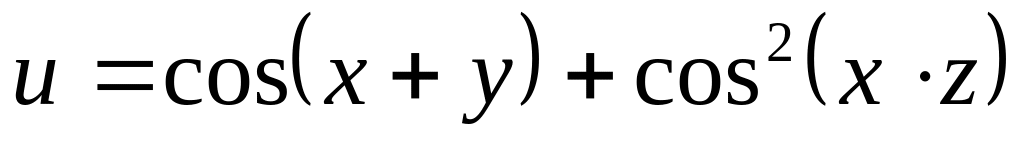
а)
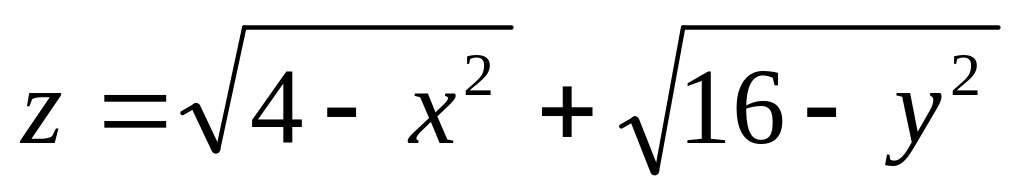 б)
б) 
а)
 б)
б) 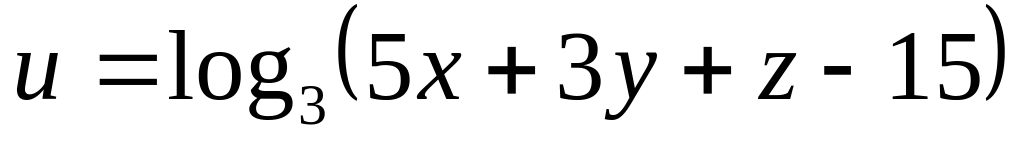
а)
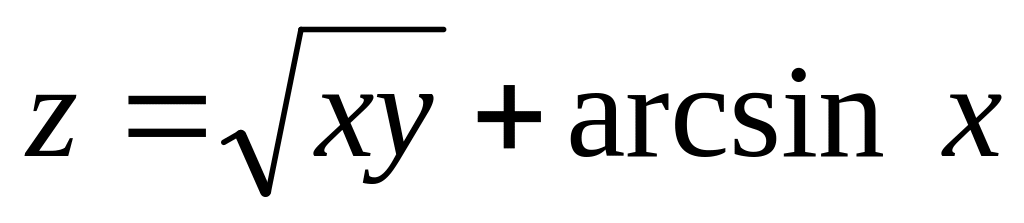 б)
б) 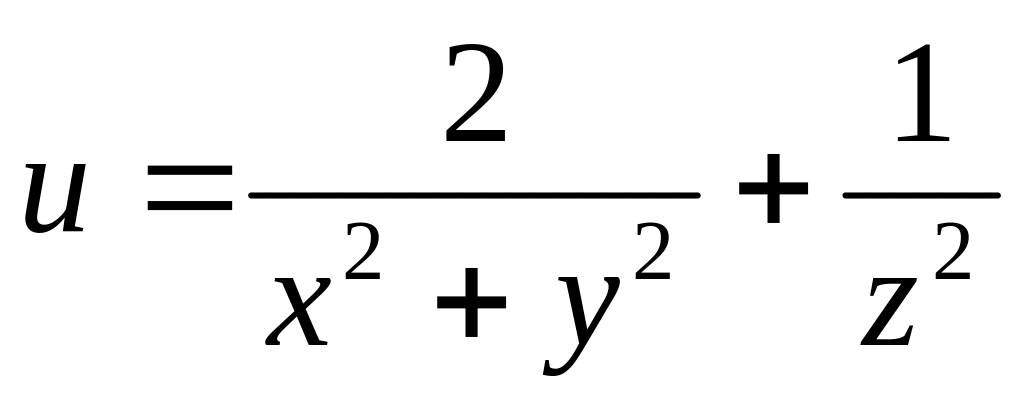
а)
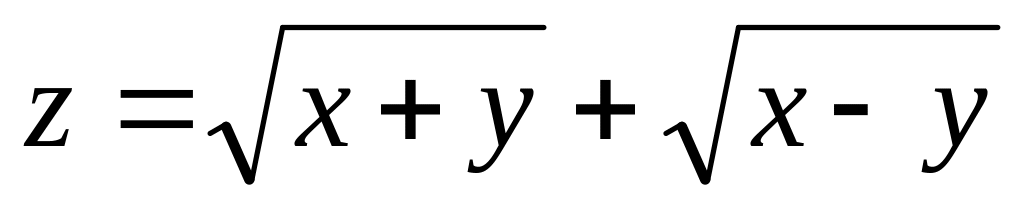 б)
б) 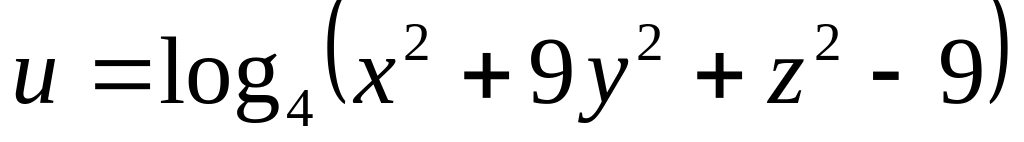
а)
 б)
б) 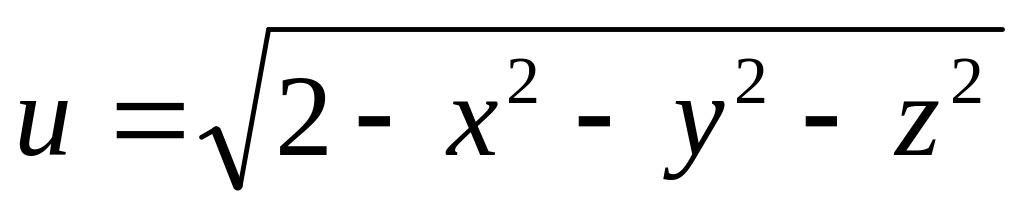
а)
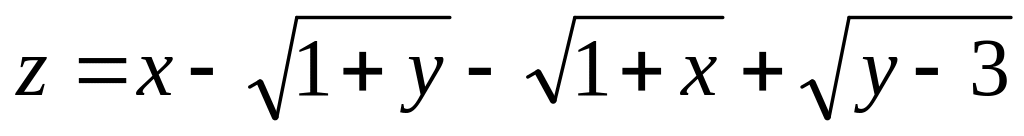 б)
б) 
а)
 б)
б) 
а)
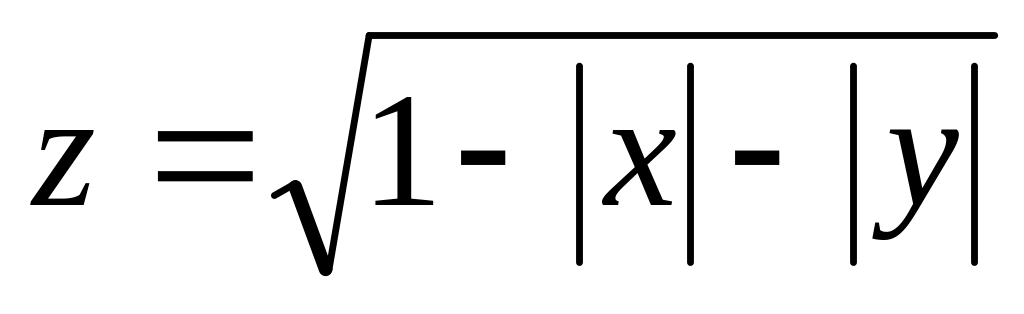 б)
б) 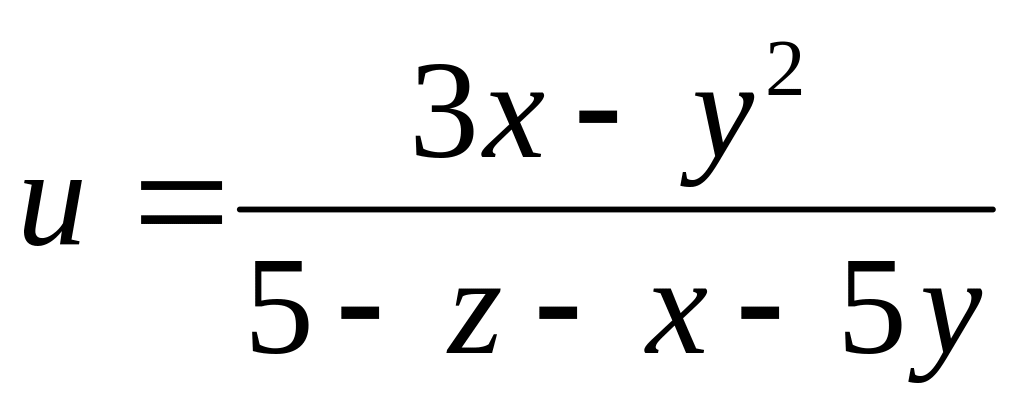
а)
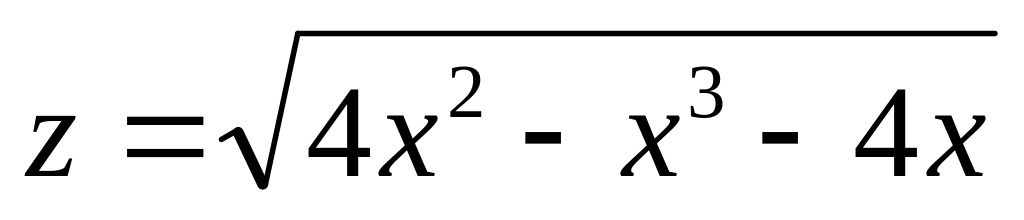 б)
б) 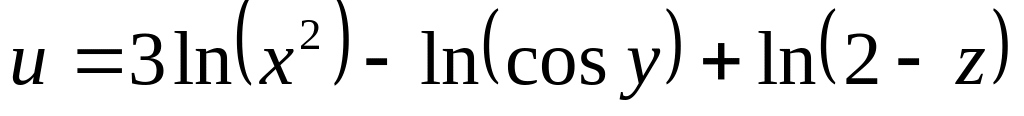
а)
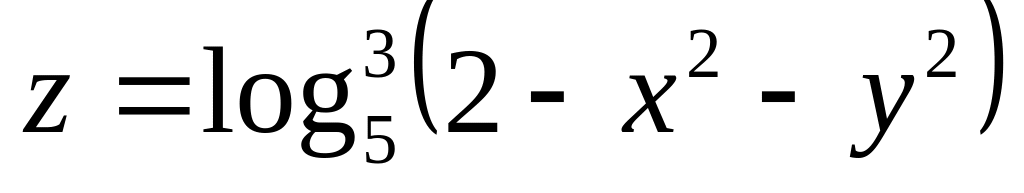 б)
б) 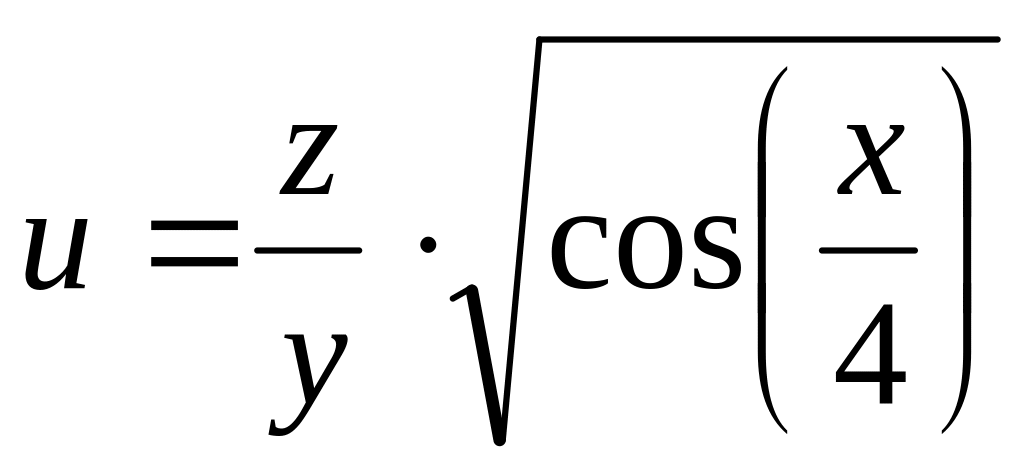
а)
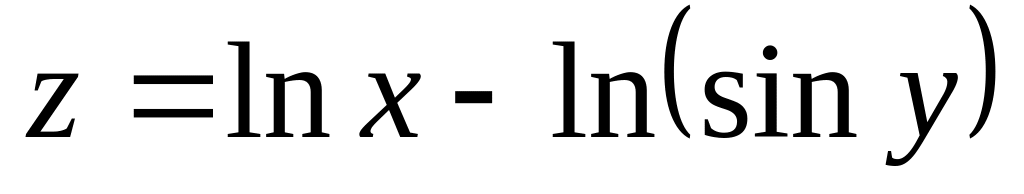 б)
б) 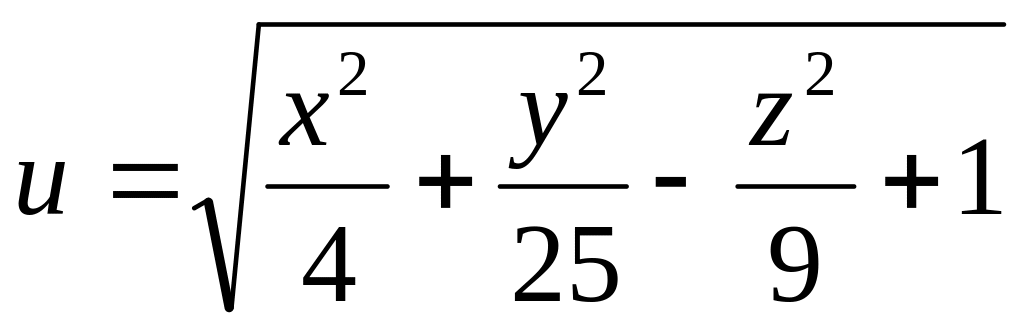
а)
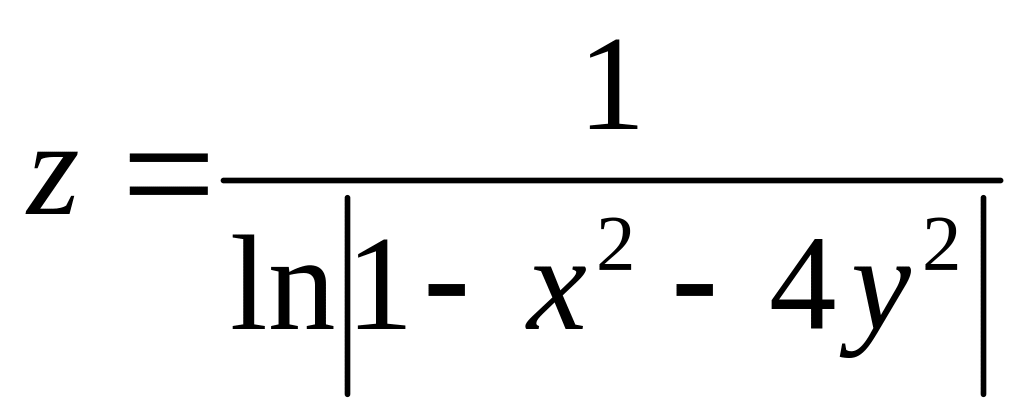 б)
б) 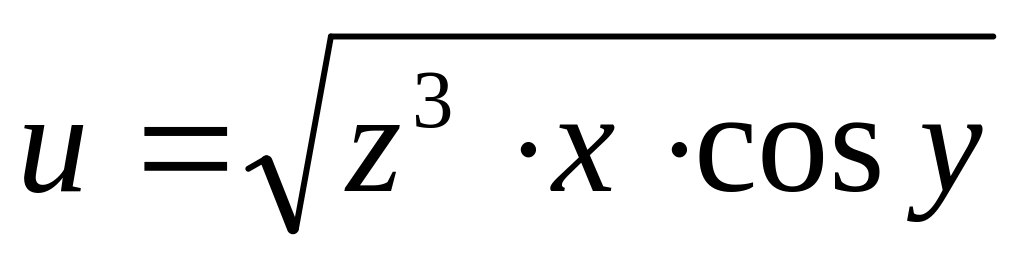
а)
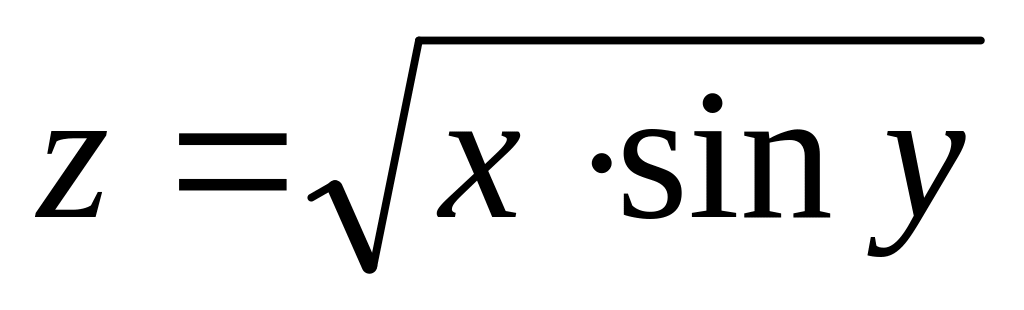 б)
б) 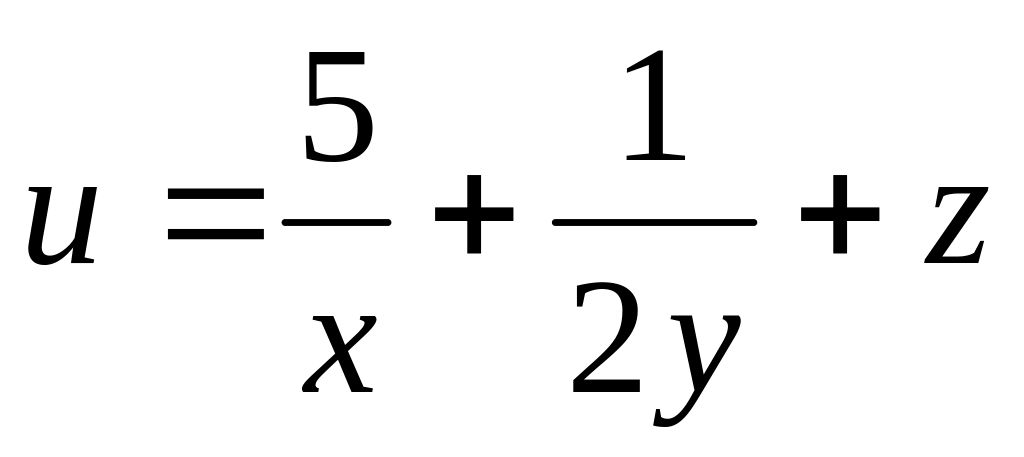
а)
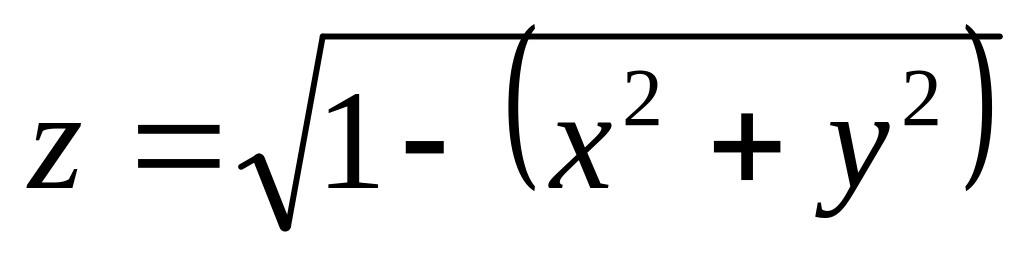 б)
б) 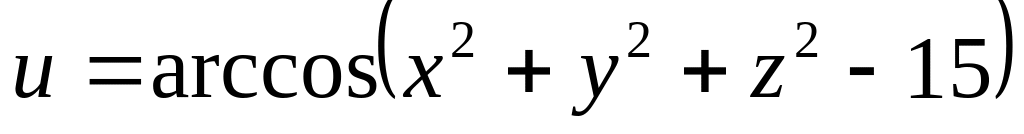
а)
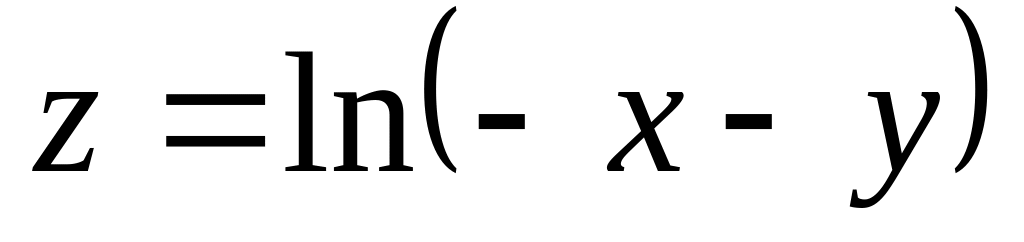 б)
б) 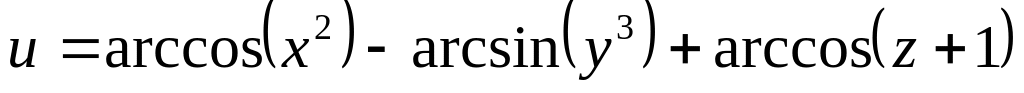
а)
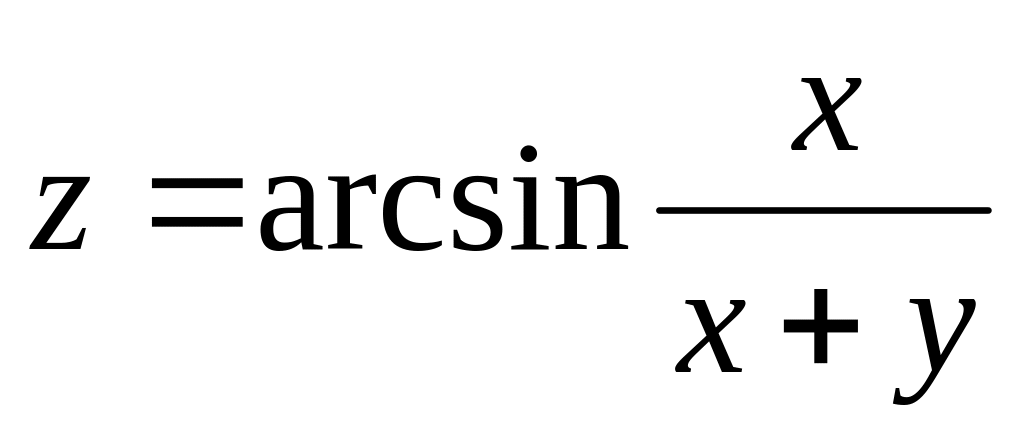 б)
б) 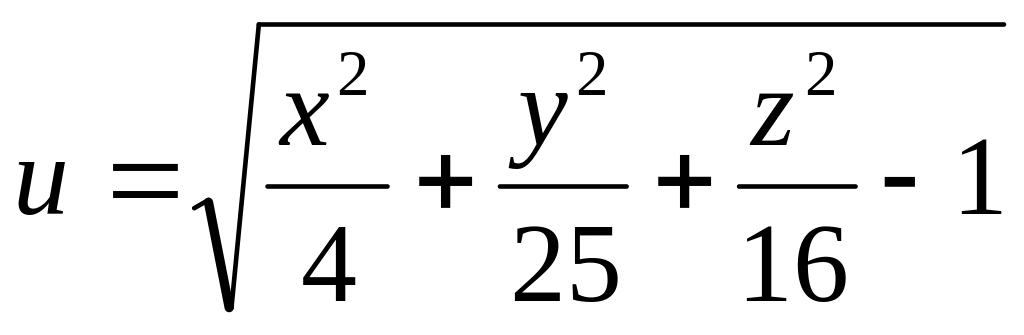
а)
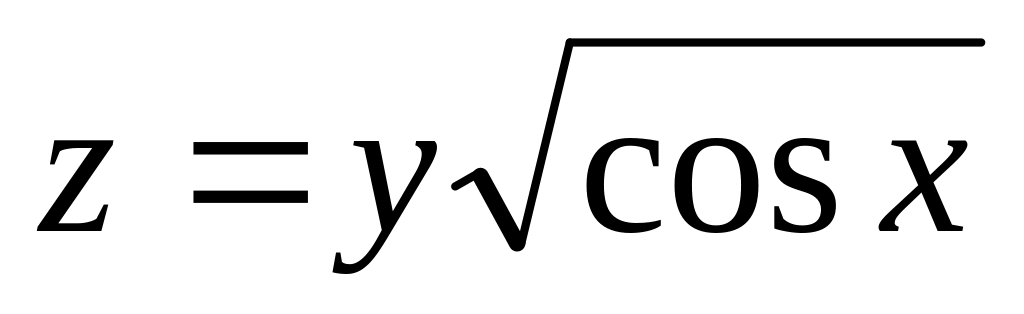 б)
б) 
Задание №2.
Найти дифференциалы первого и второго порядков функция нескольких переменных.
а)
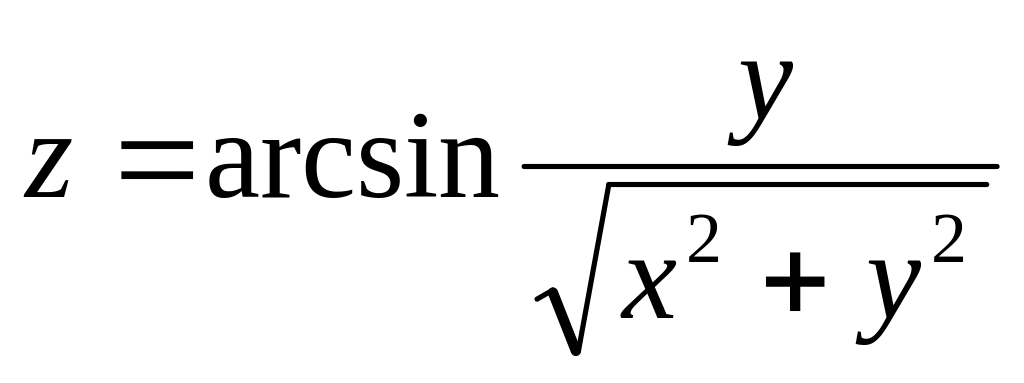 б)
б) 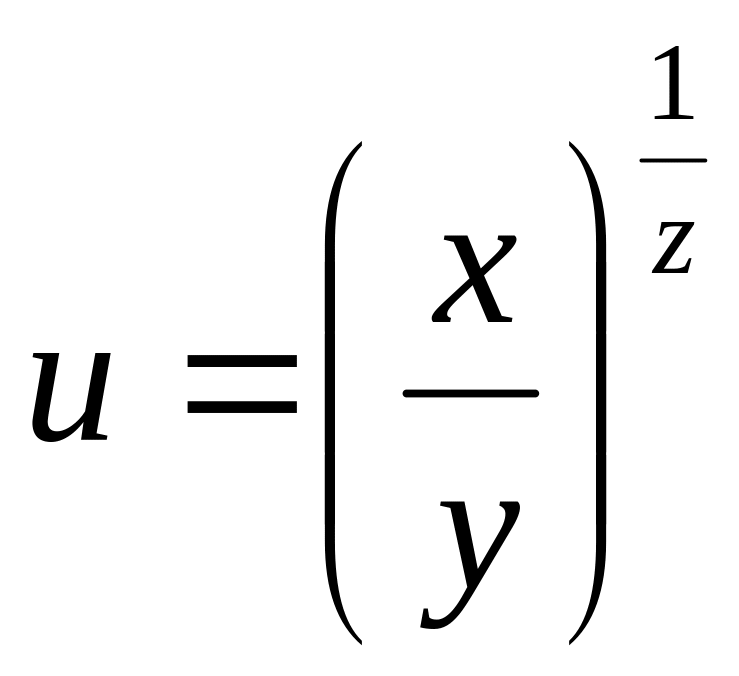
а)
 б)
б) 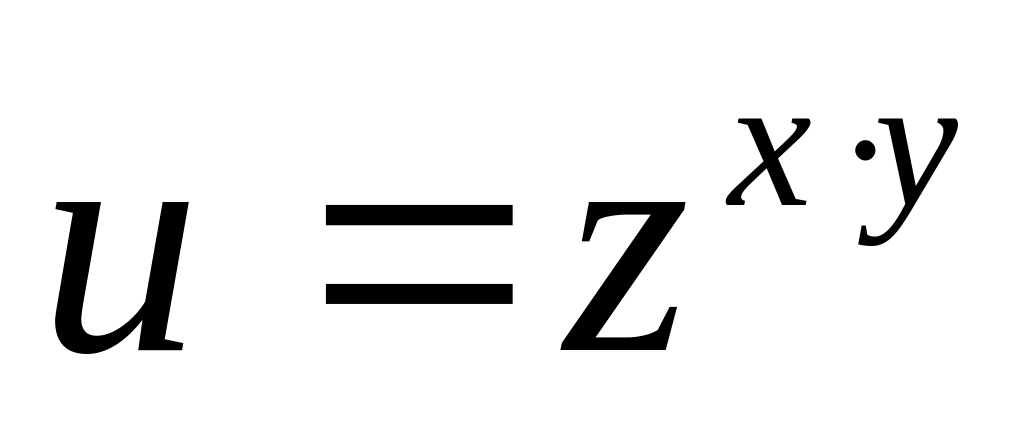
а)
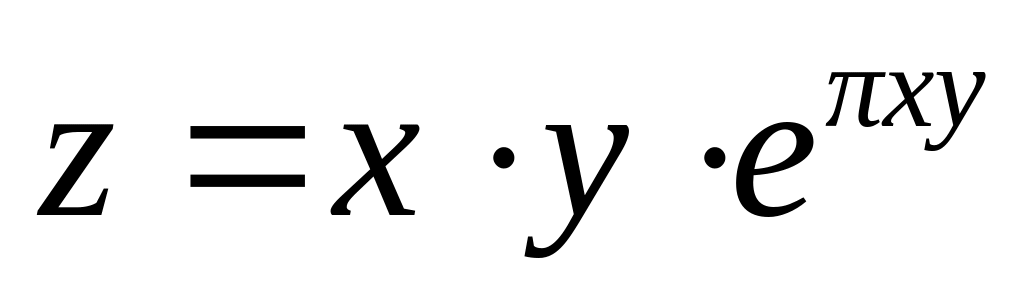 б)
б) 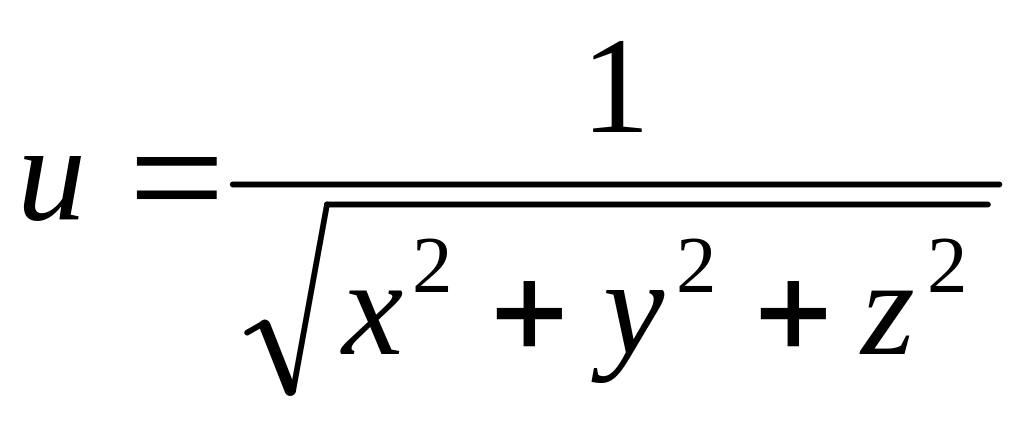
а)
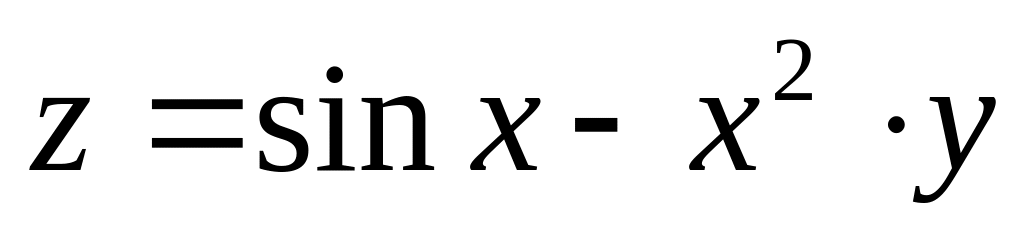 б)
б) 
а)
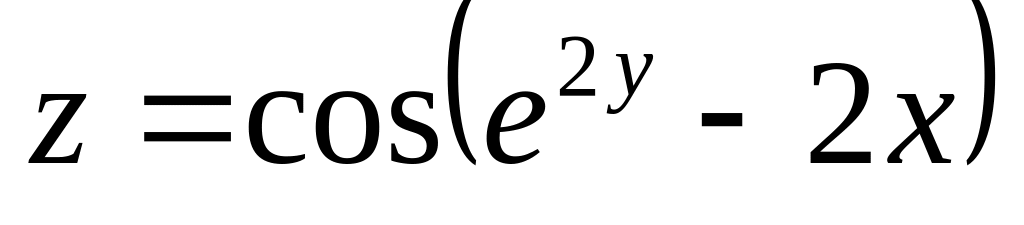 б)
б) 
а)
 б)
б) 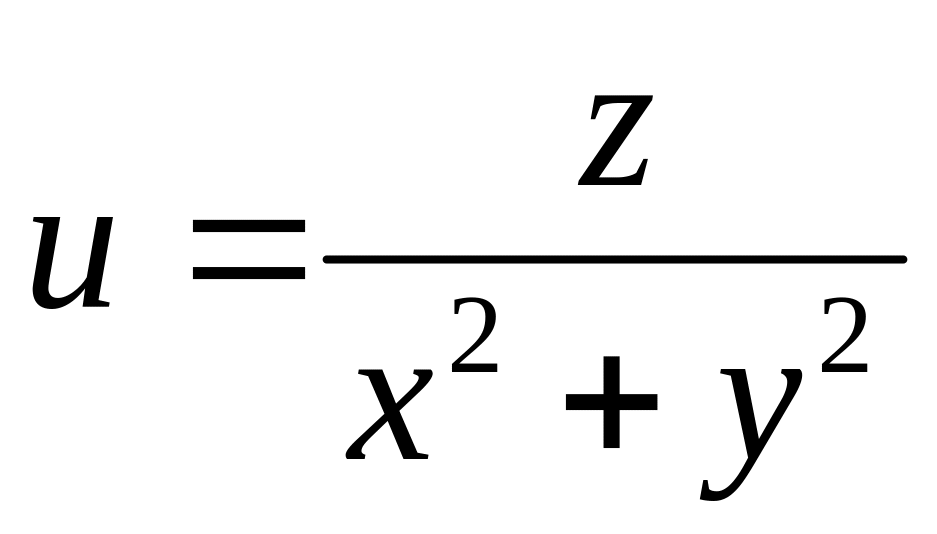
а)
 б)
б) 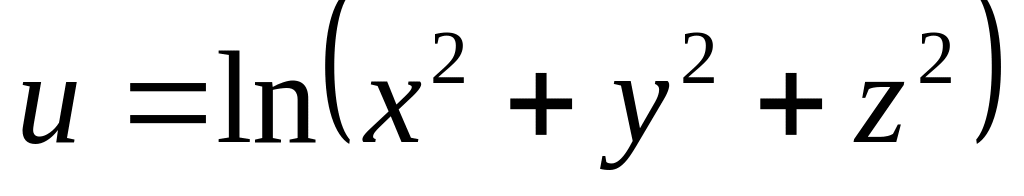
а)
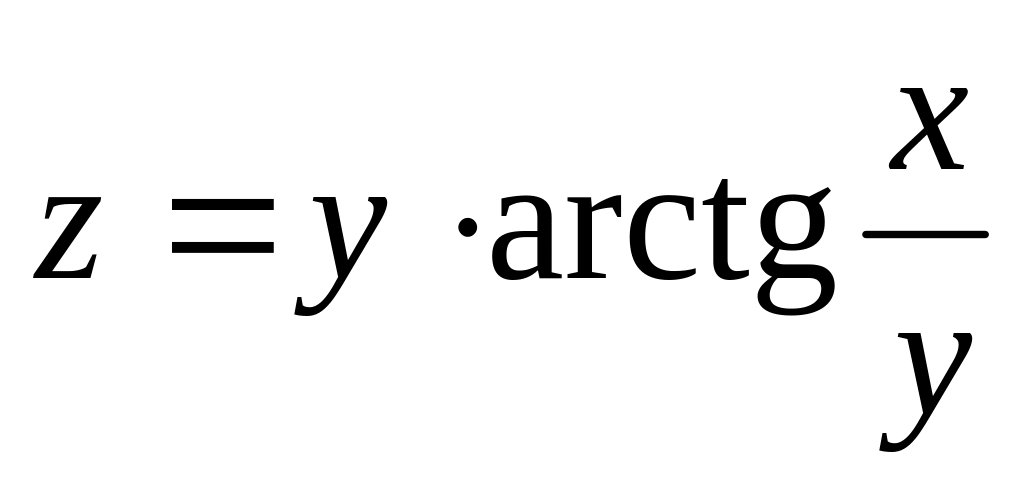 б)
б) 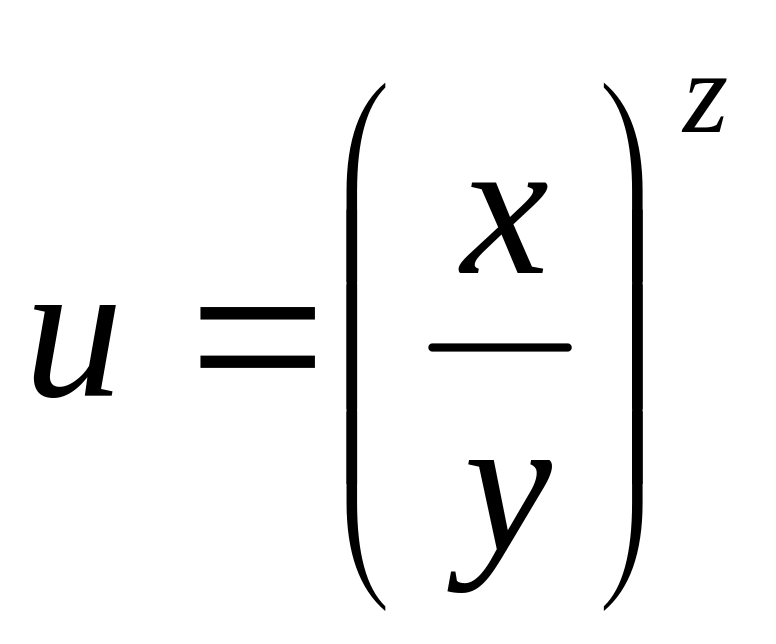
а)
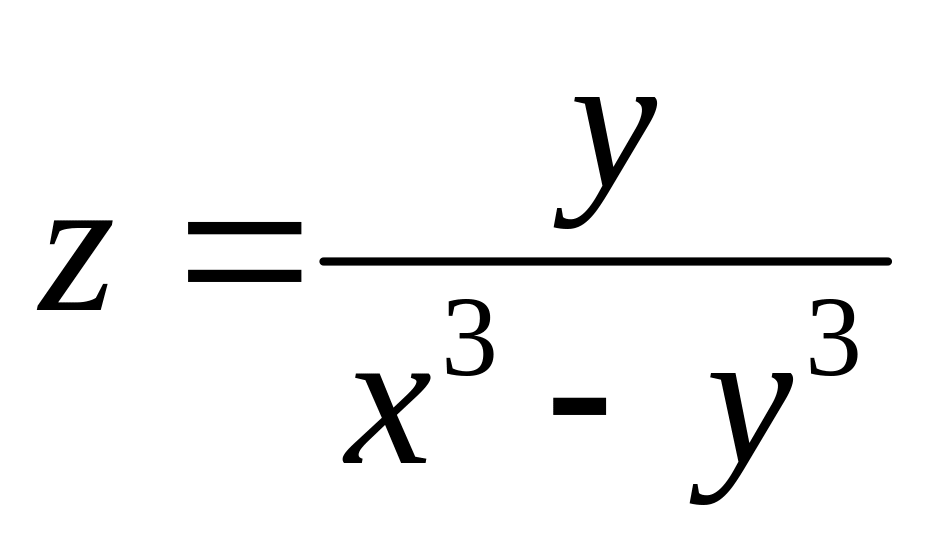 б)
б) 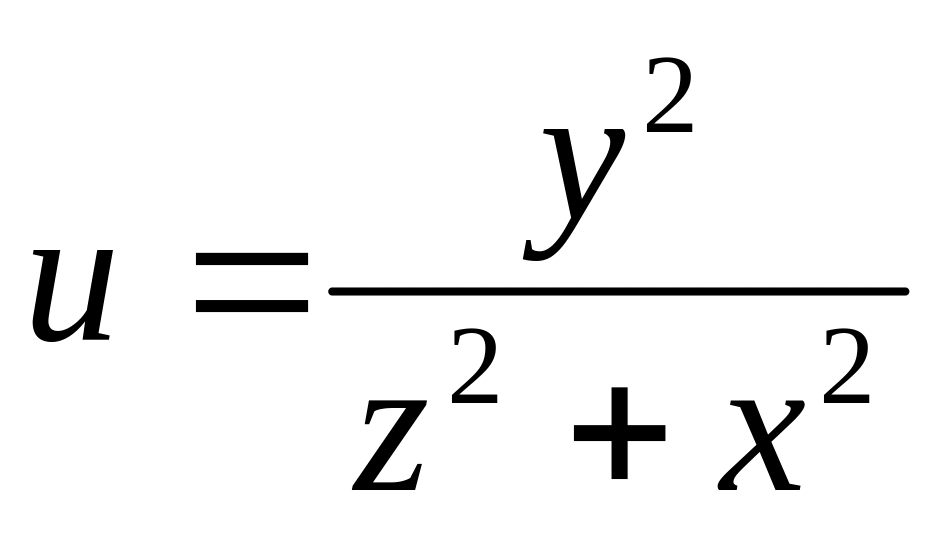
а)
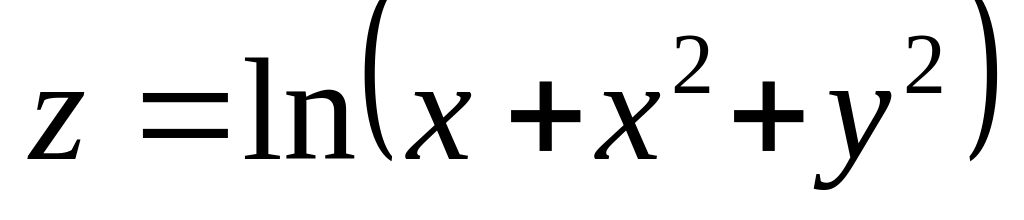 б)
б) 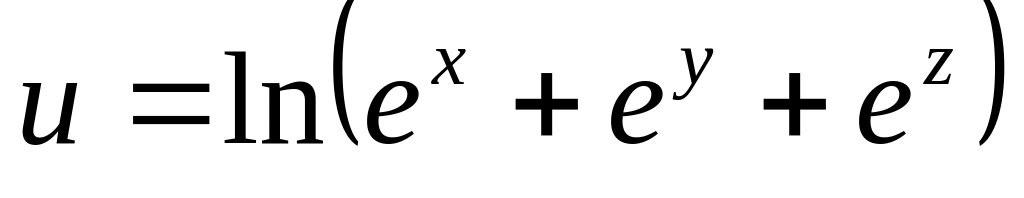
а)
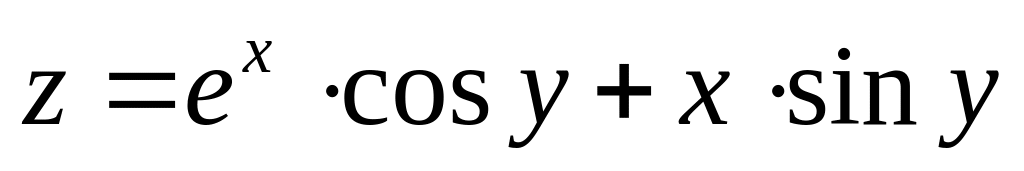 б)
б) 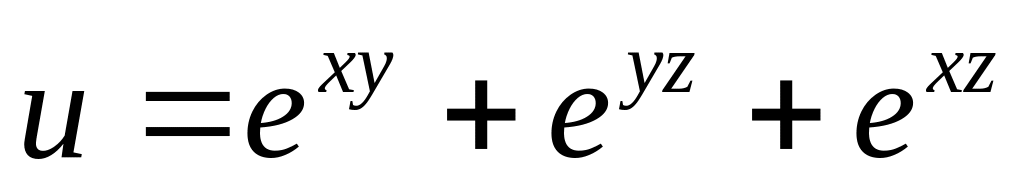
а)
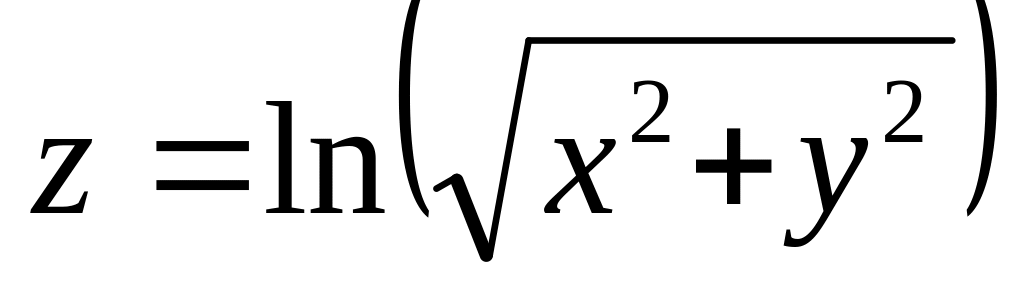 б)
б) 
а)
 б)
б) 
а)
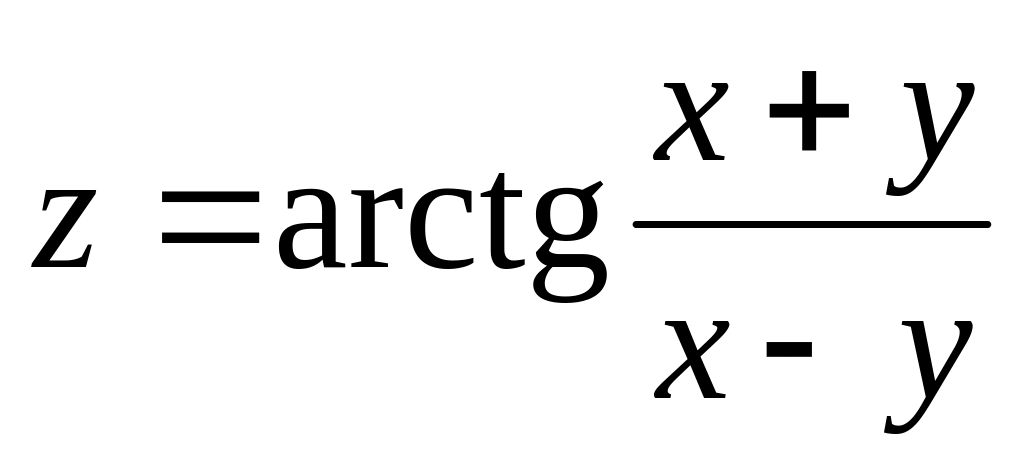 б)
б) 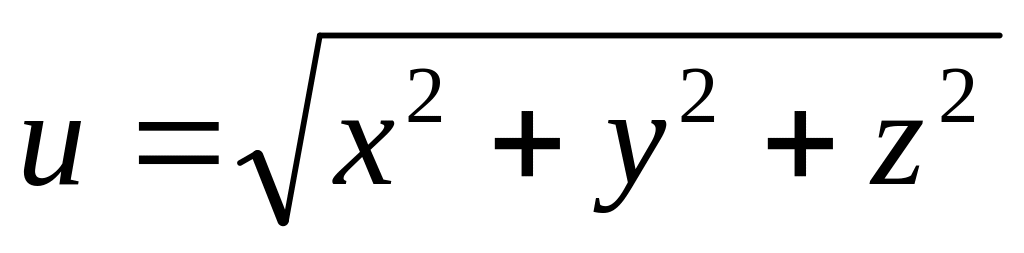
а)
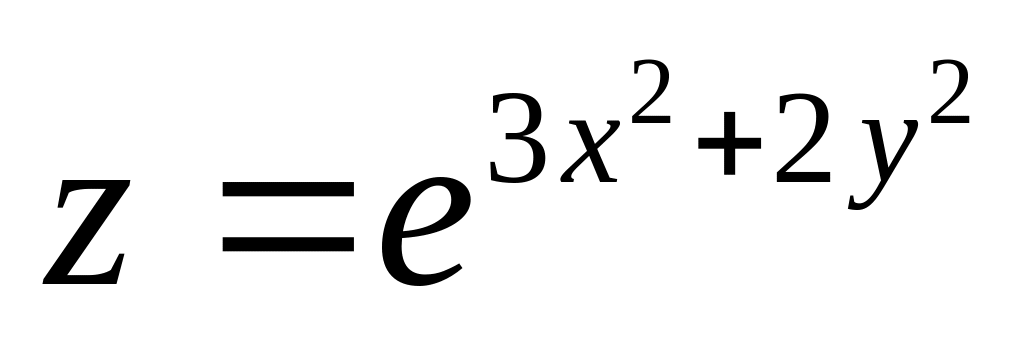 б)
б) 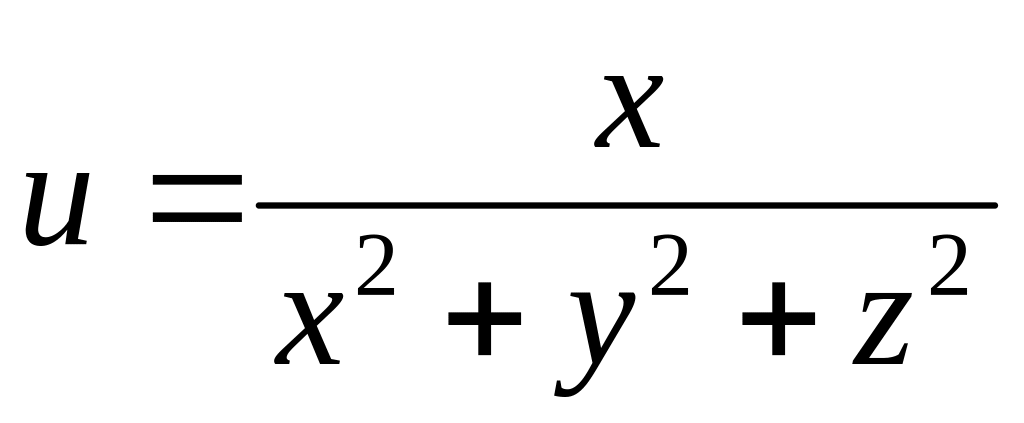
а)
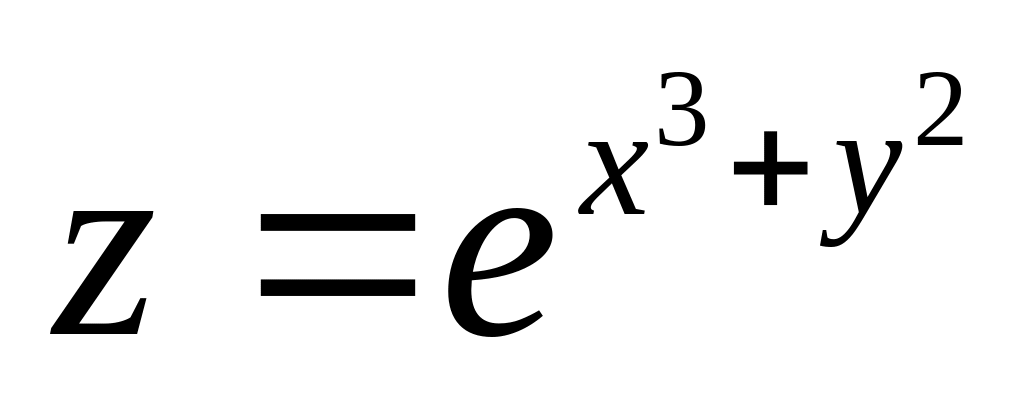 б)
б)
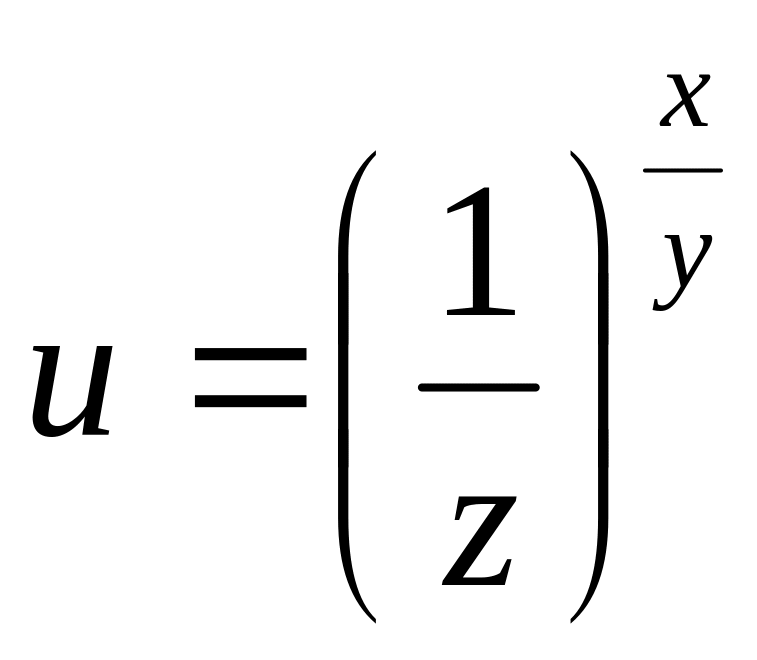
а)
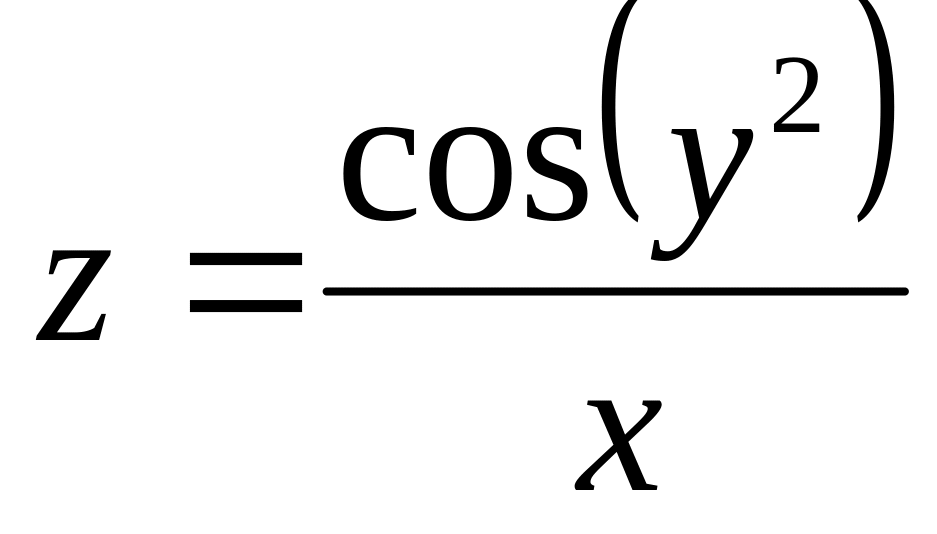 б)
б) 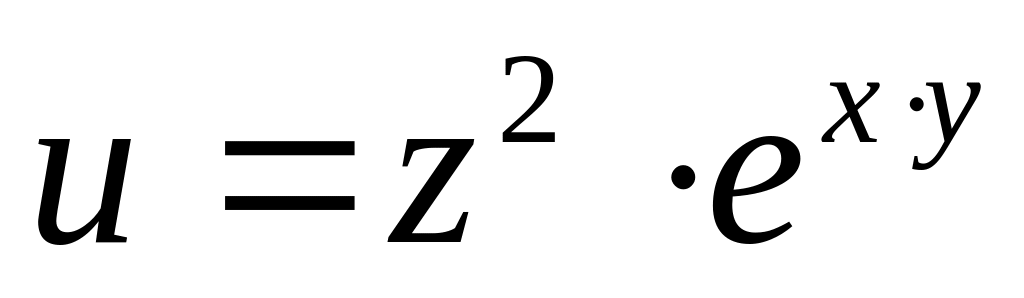
а)
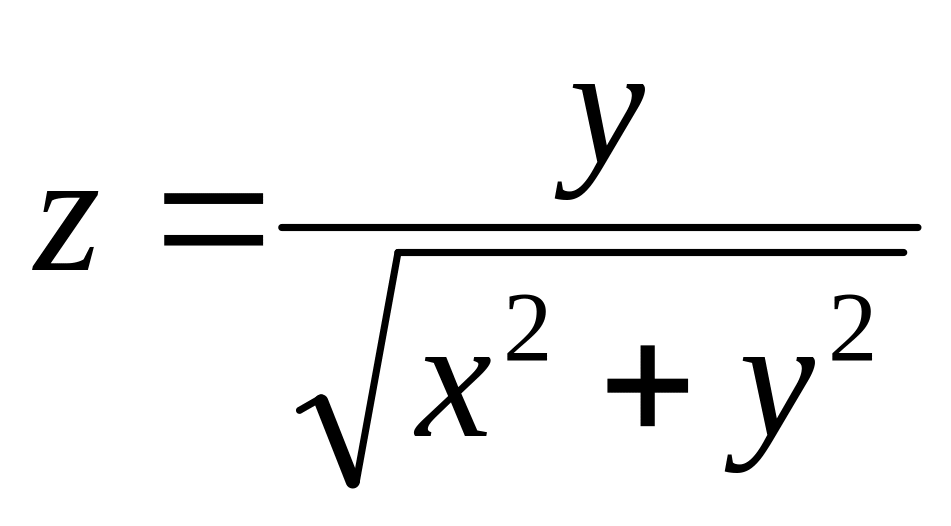 б)
б) 
а)
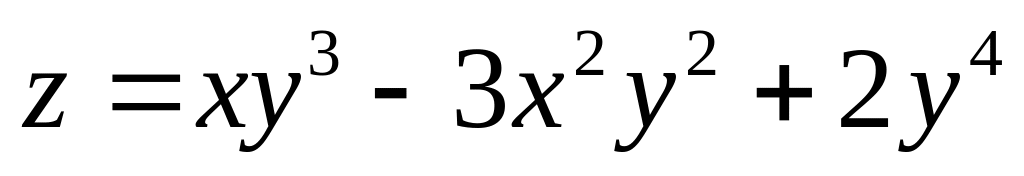 б)
б) 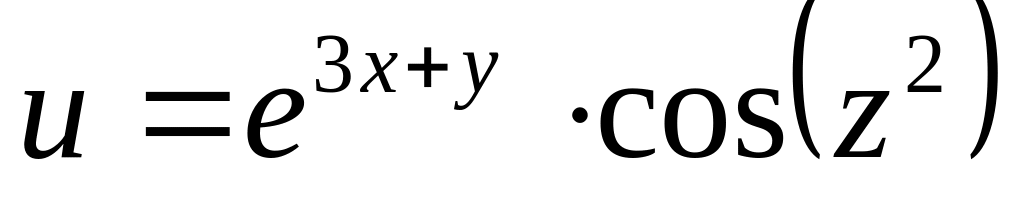
а)
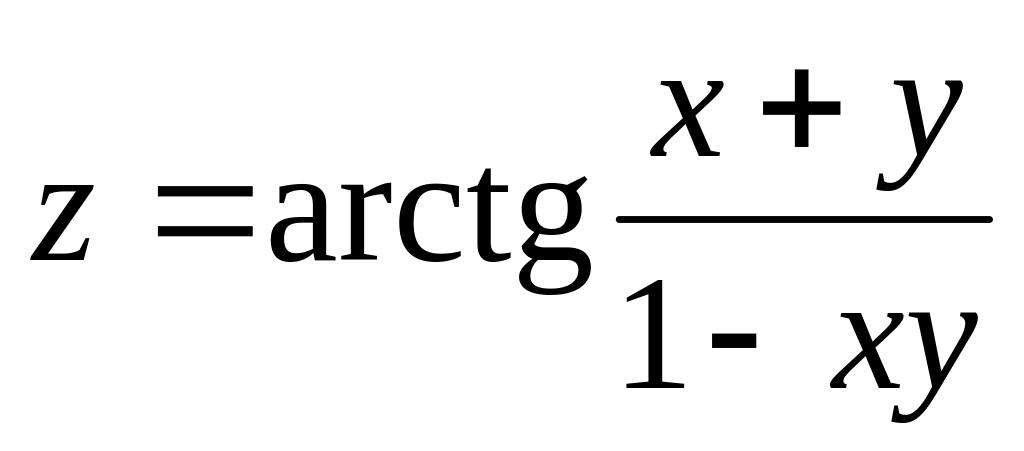 б)
б)
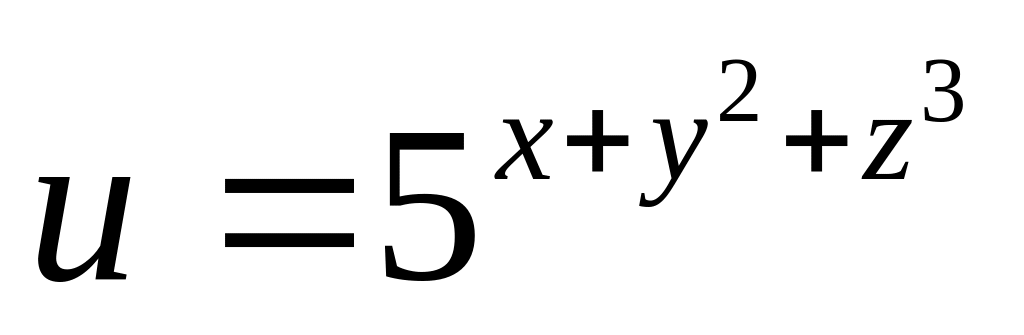
а)
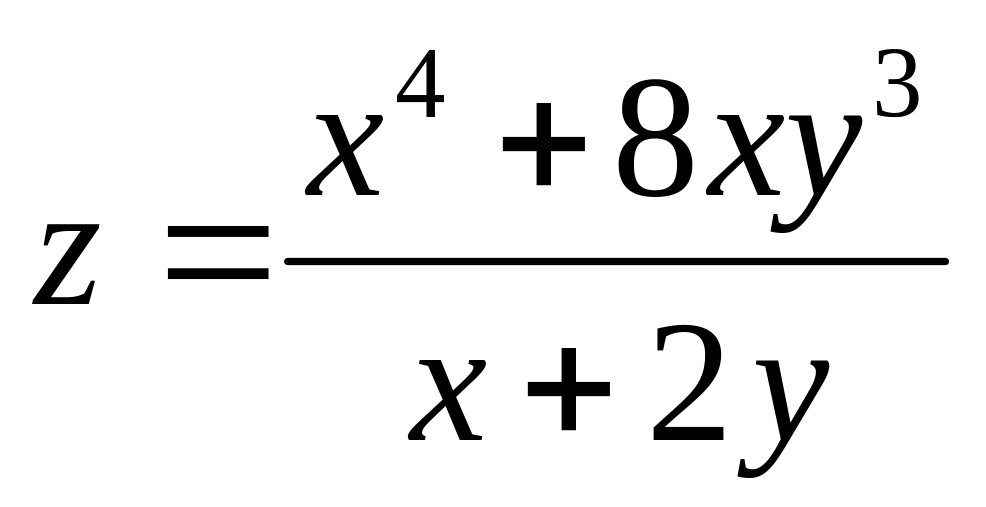 б)
б) 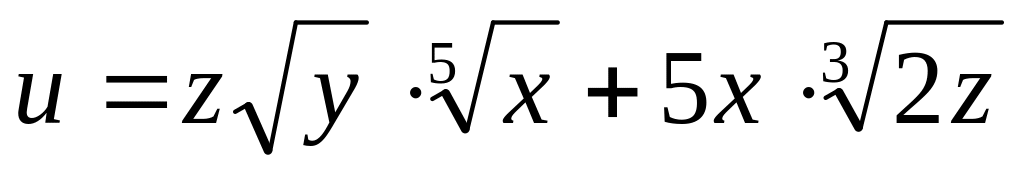
а)
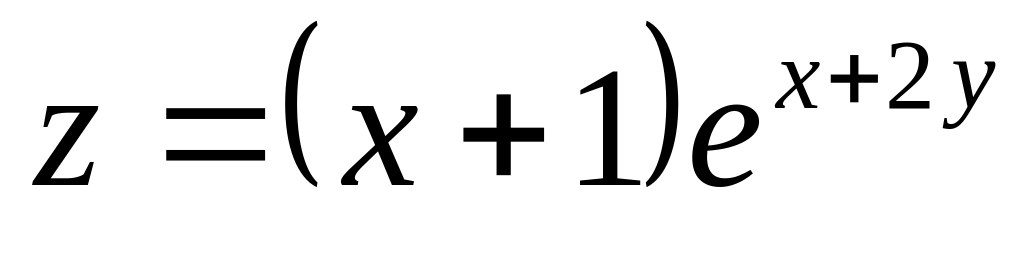 б)
б) 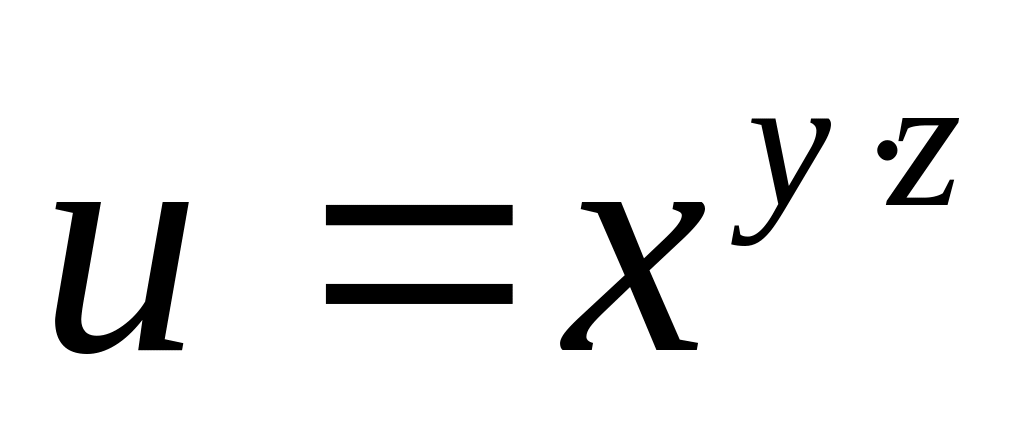
а)
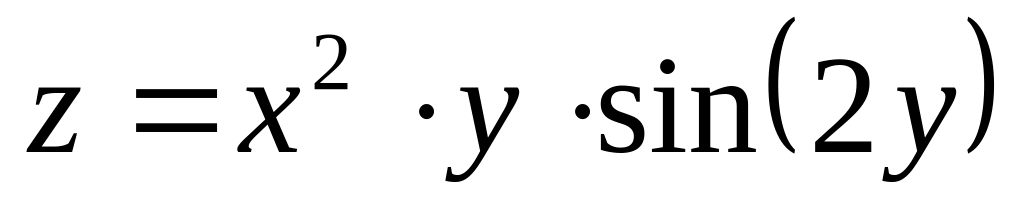 б)
б) 
а)
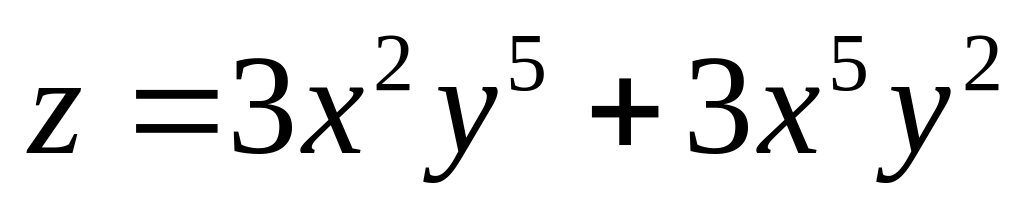 б)
б) 
а)
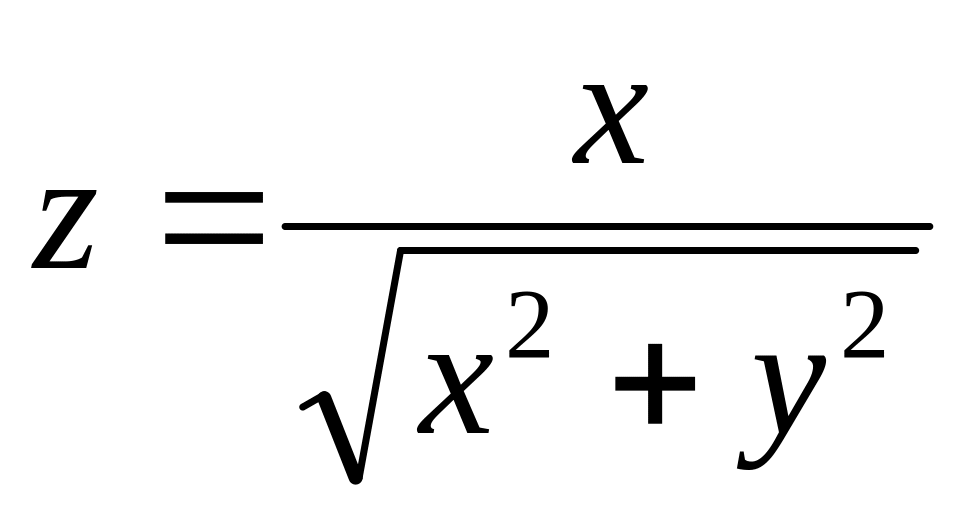 б)
б) 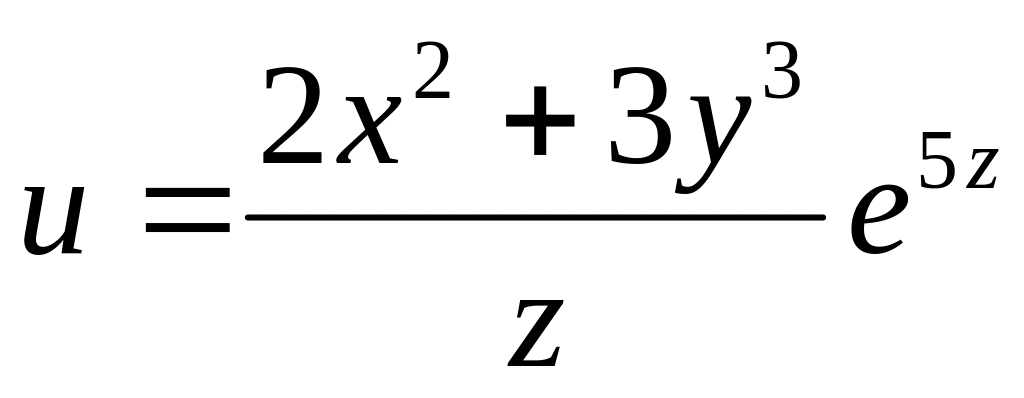
а)
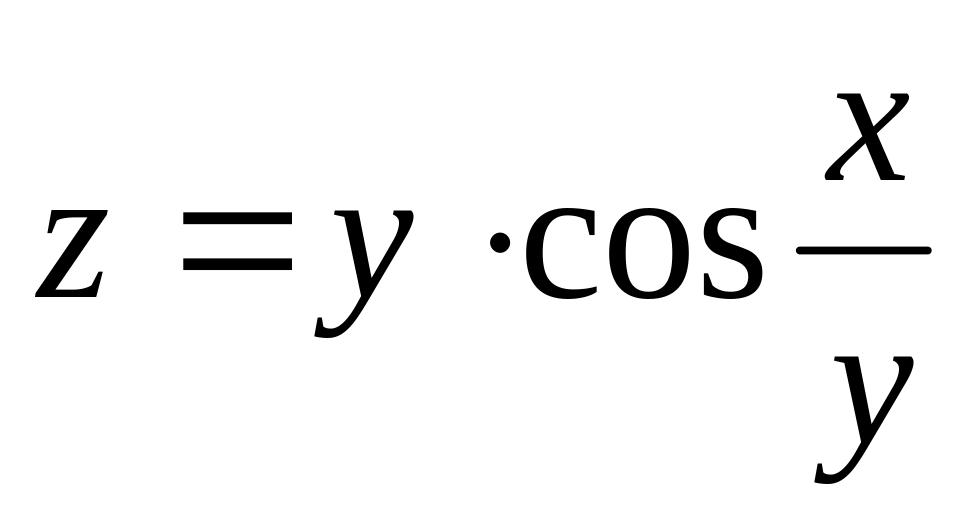 б)
б) 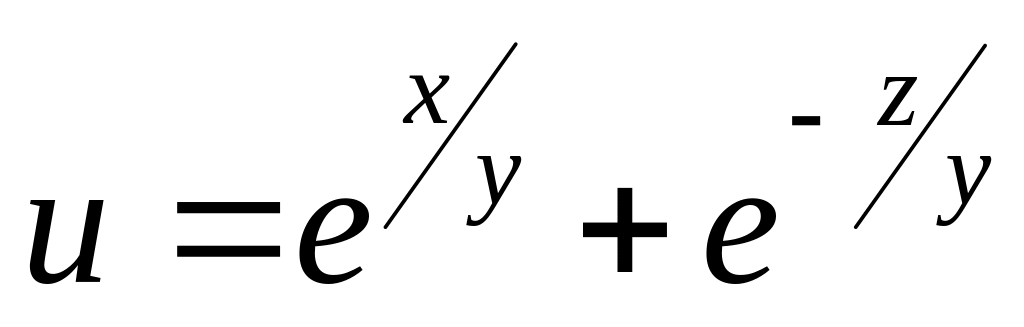
а)
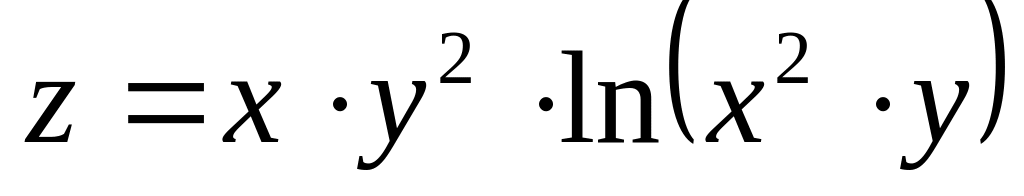 б)
б) 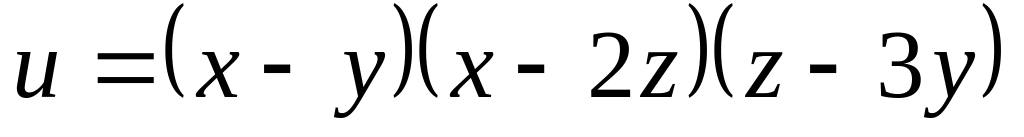
а)
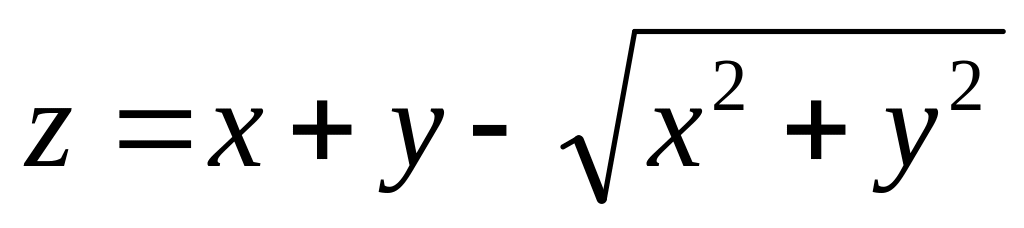 б)
б) 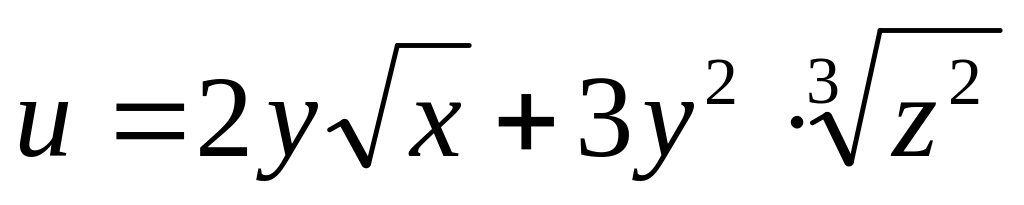
а)
 б)
б) 
а)
 б)
б) 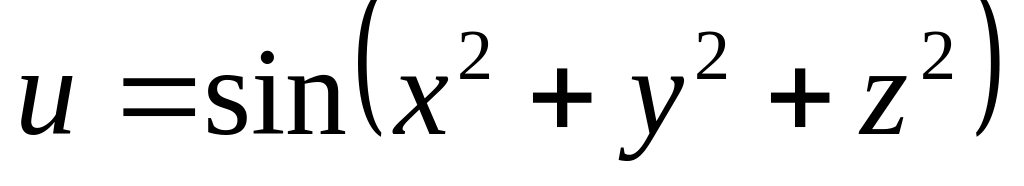
Задание№3.
Вычислить
приближенно (считая![]() ).
).
Задание№4.
Дана сложная функция. Найти
а)
![]() ,
если
,
если
![]() ;
;
б)
![]() и
и
![]() ,
если
,
если
![]() .
.
а)
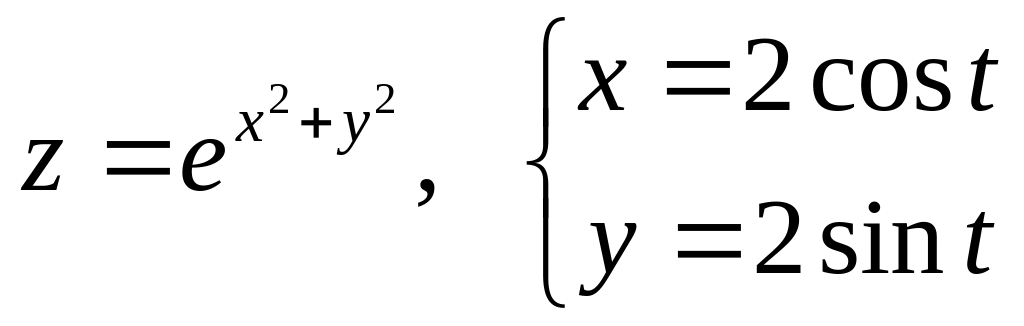 б)
б) 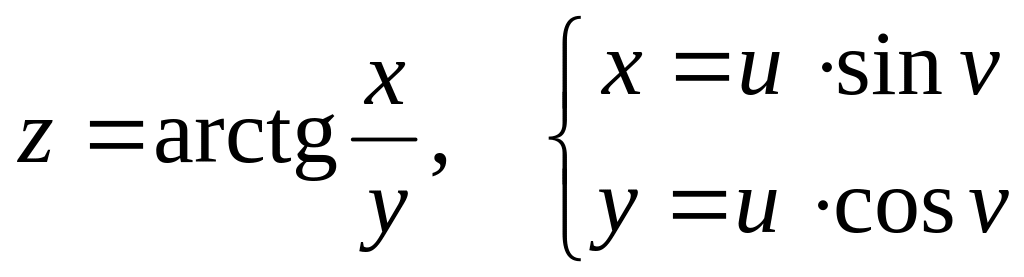
а)
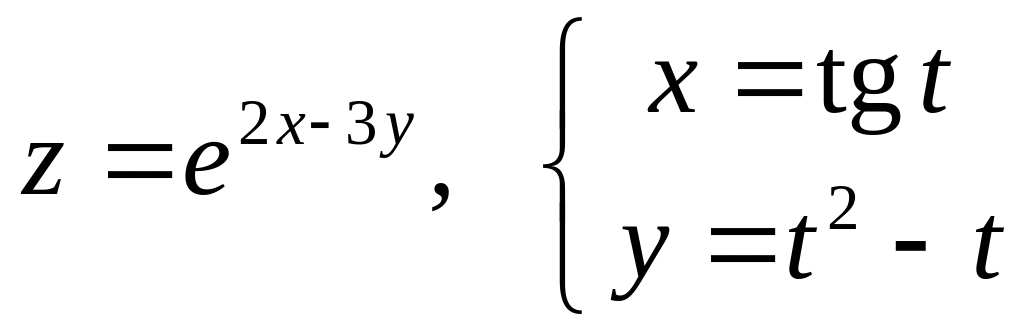 б)
б) 
а)
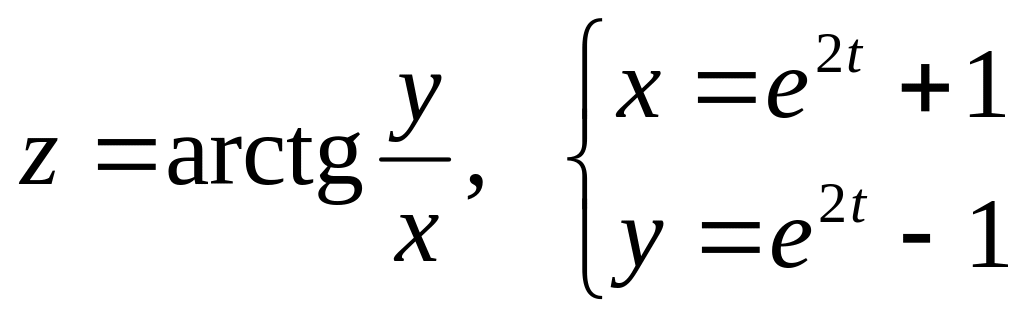 б)
б) 
а)
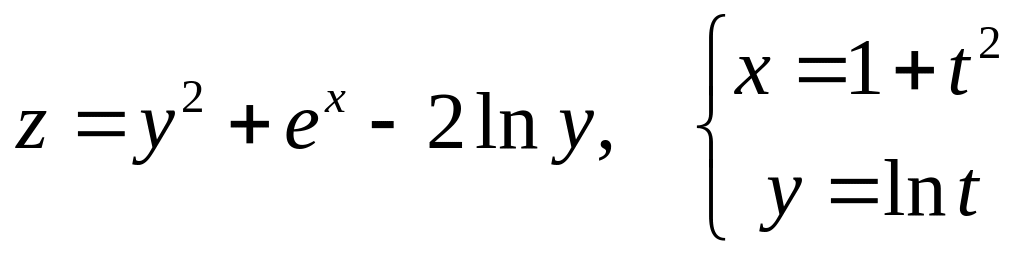 б)
б) 
а)
 б)
б) 
а)
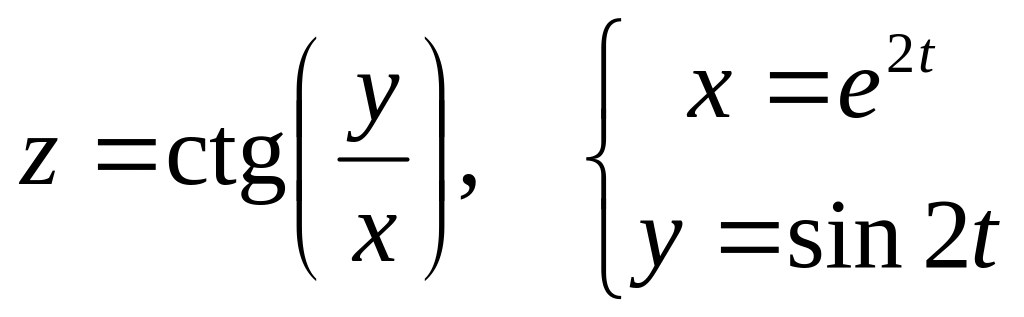 б)
б) 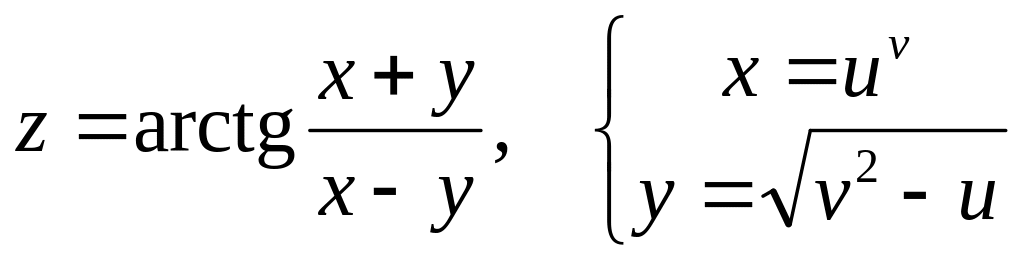
а)
 б)
б) 
а)
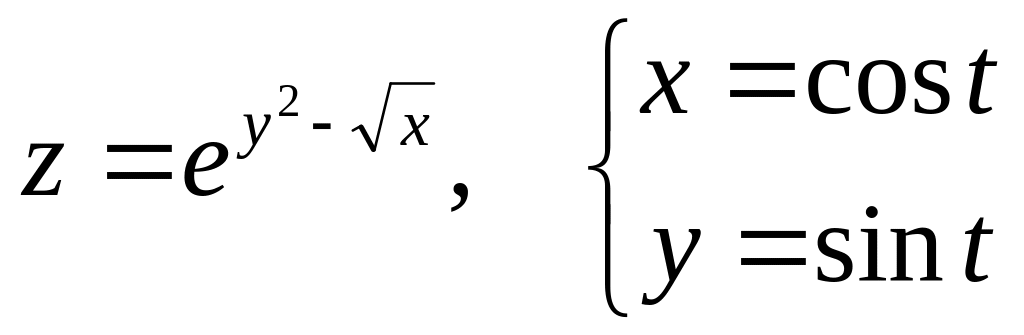 б)
б) 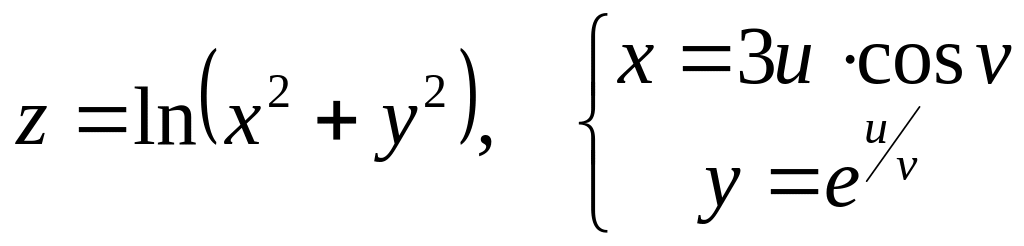
а)
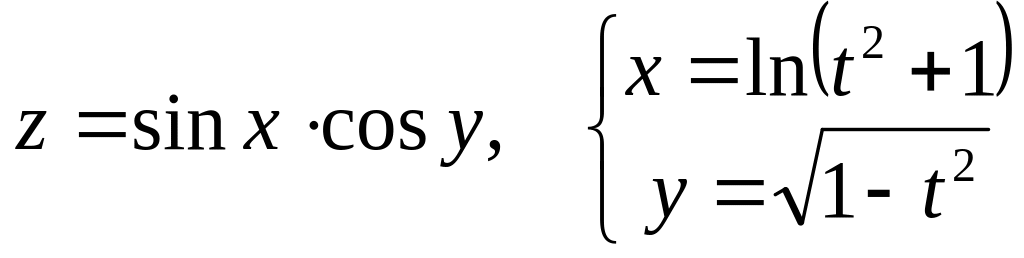 б)
б) 
а)
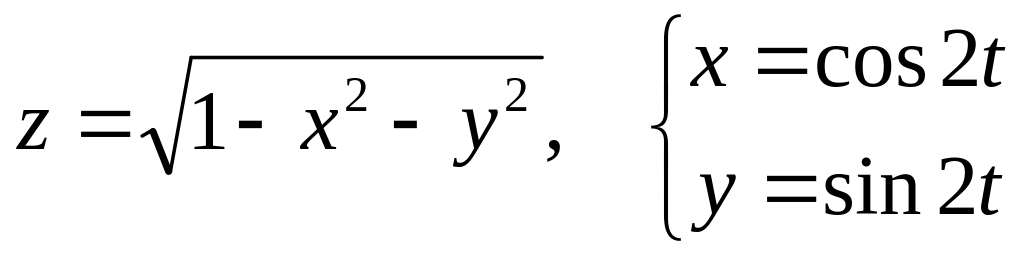 б)
б) 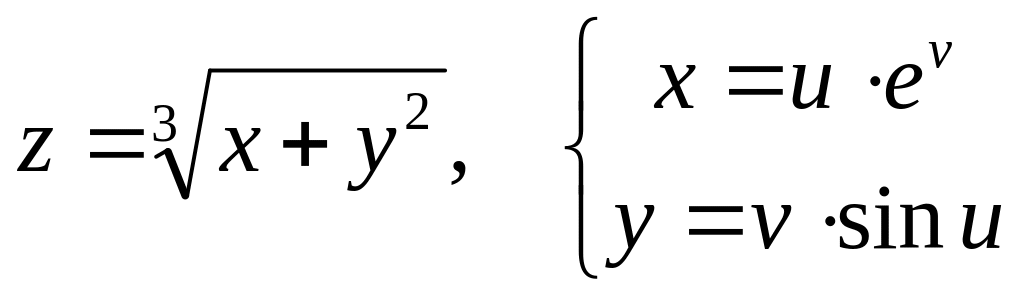
а)
 б)
б) 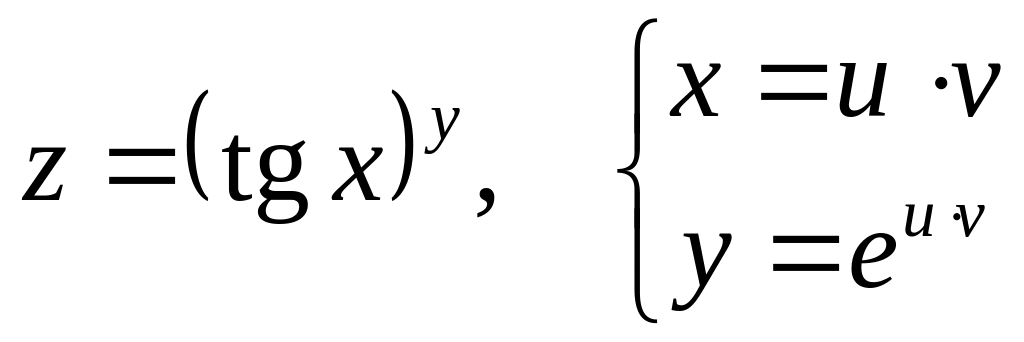
а)
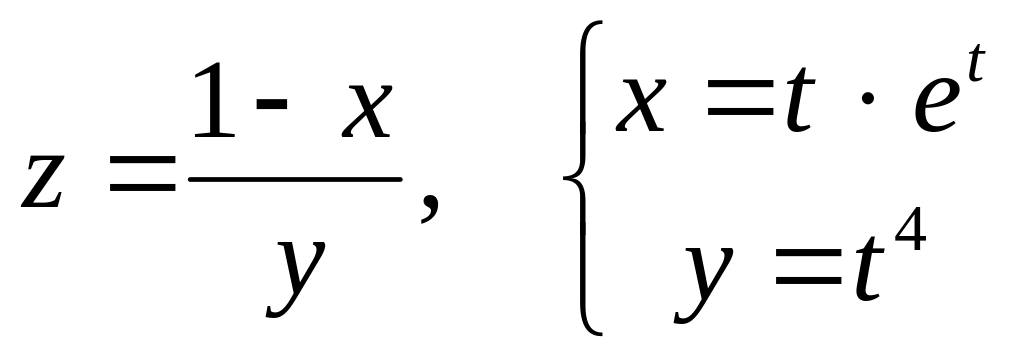 б)
б) 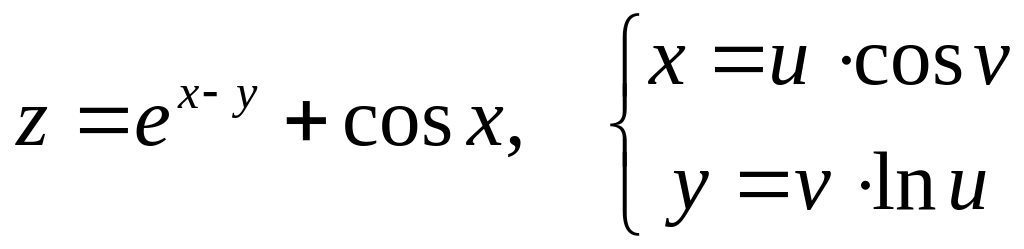
а)
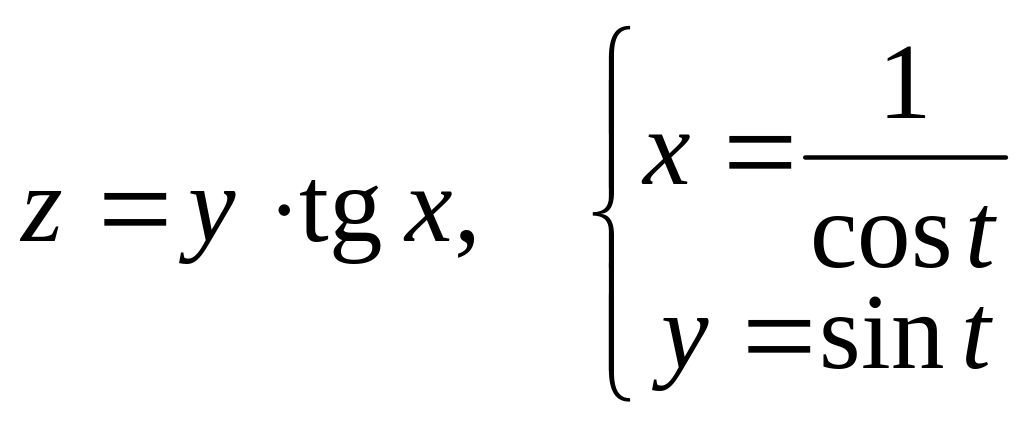 б)
б) 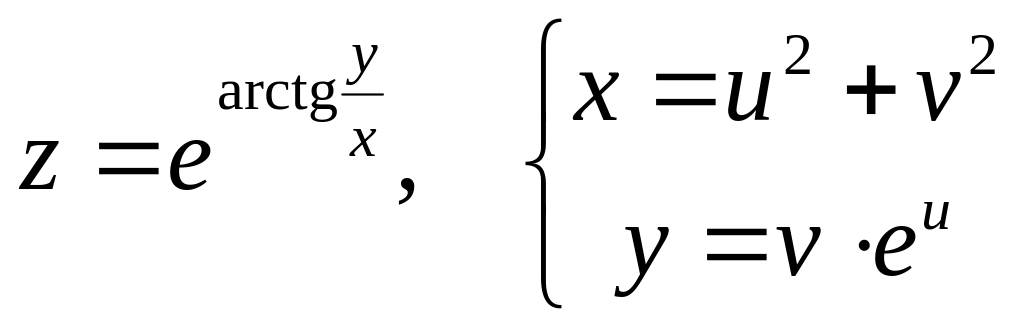
а)
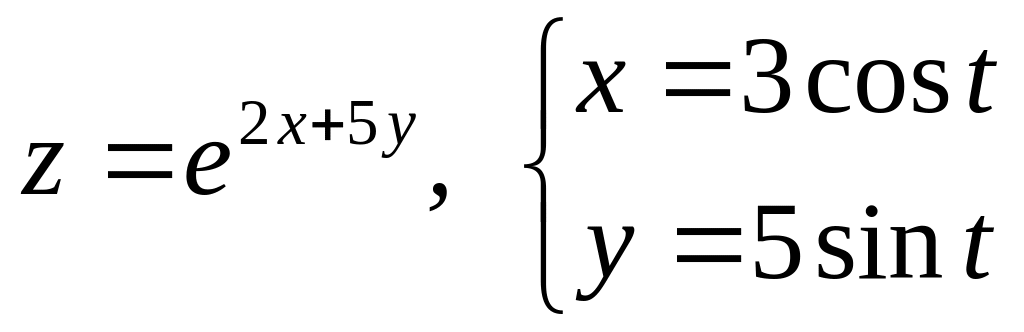 б)
б) 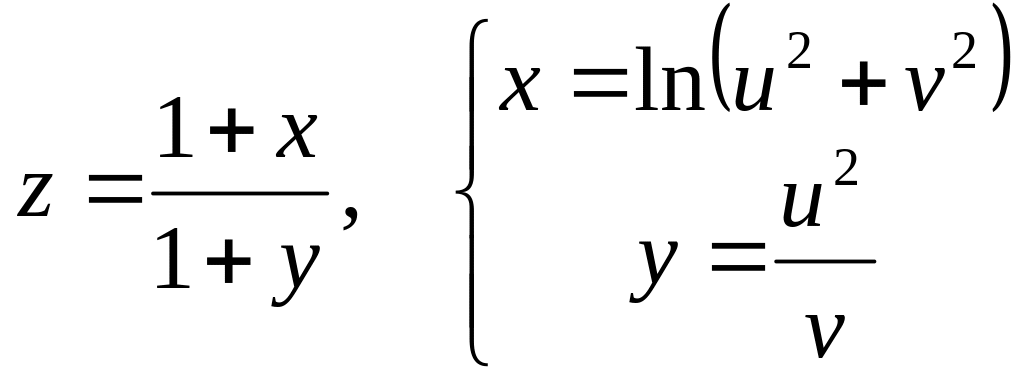
а)
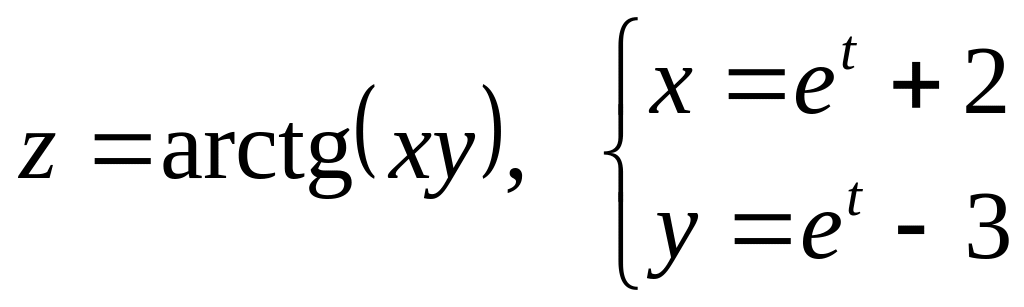 б)
б) 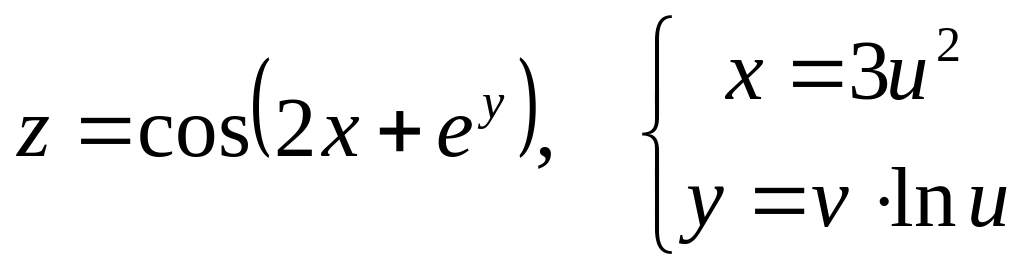
а)
 б)
б) 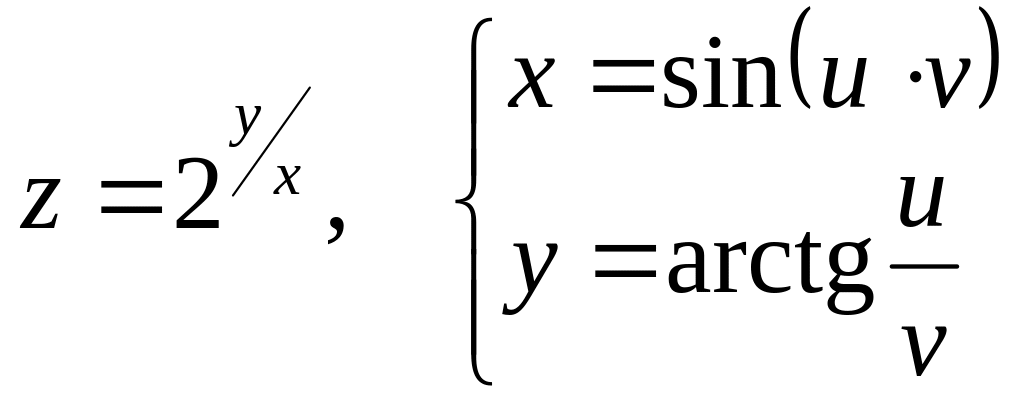
а)
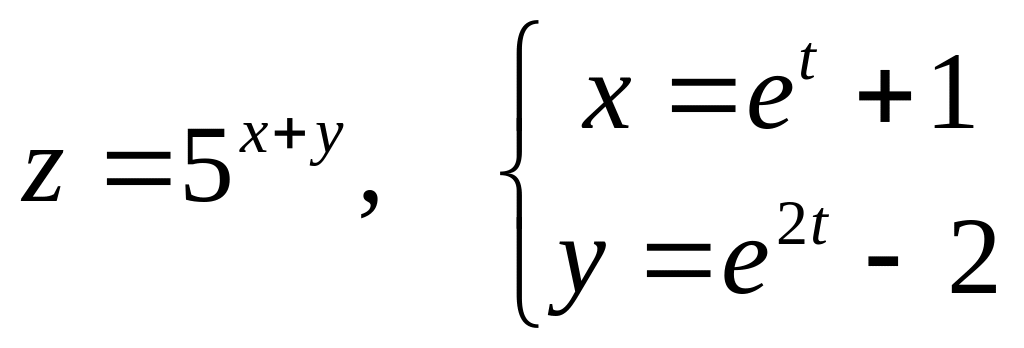 б)
б) 
а)
 б)
б) 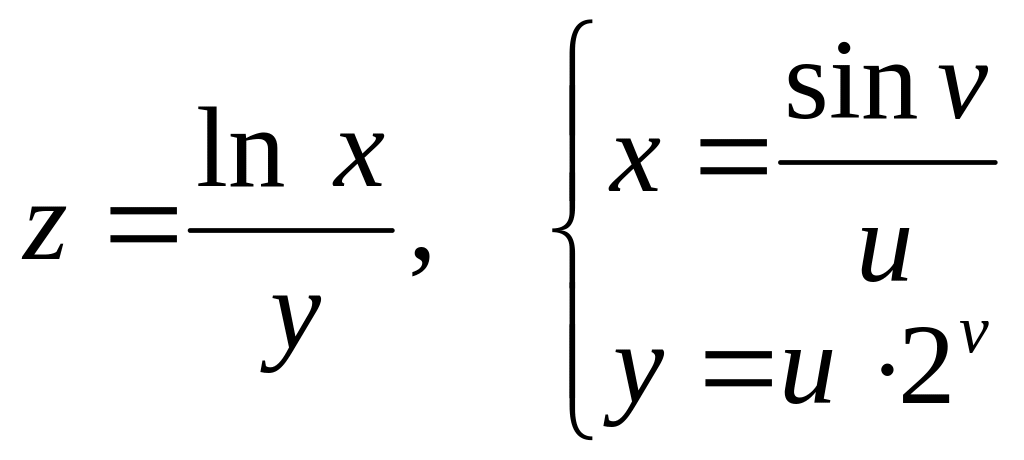
а)
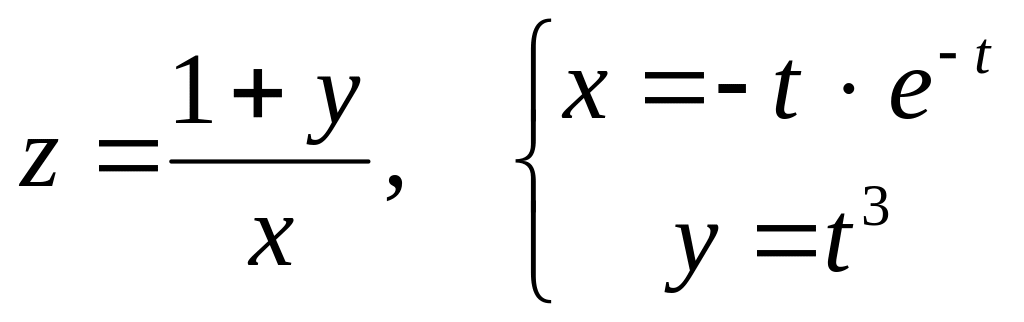 б)
б) 
а)
 б)
б) 
а)
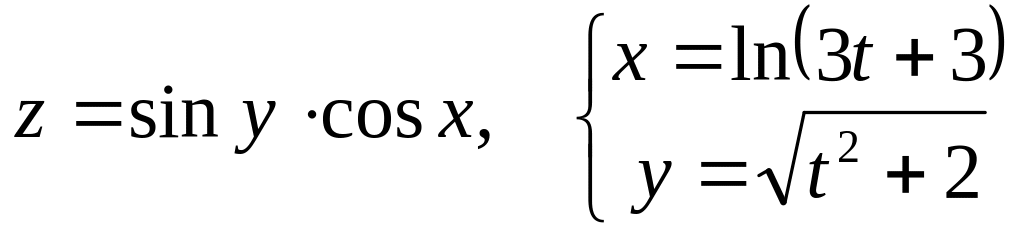 б)
б) 
а)
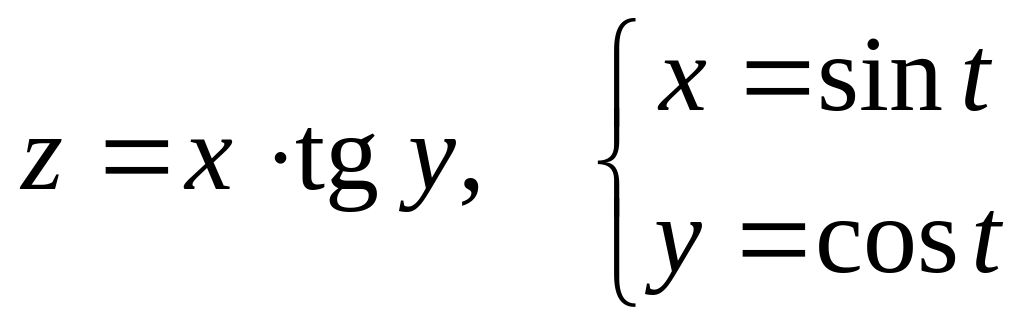 б)
б) 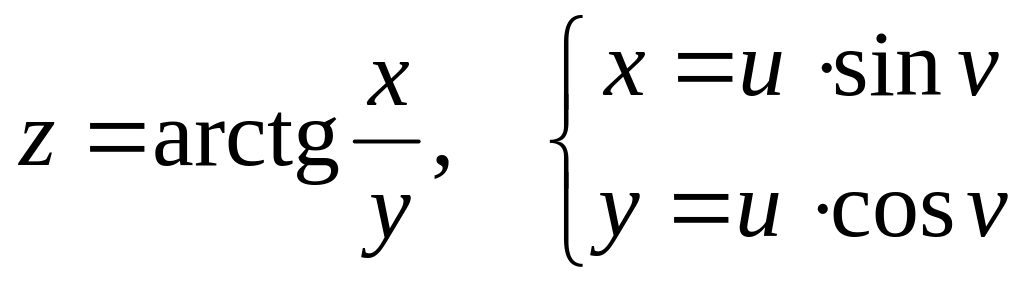
а)
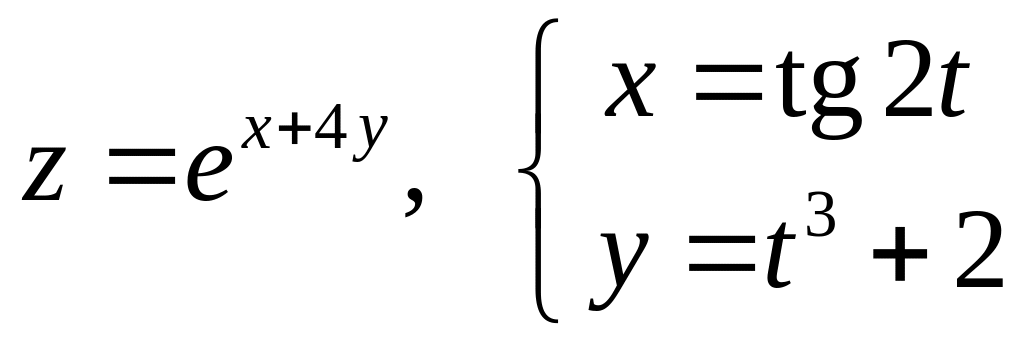 б)
б) 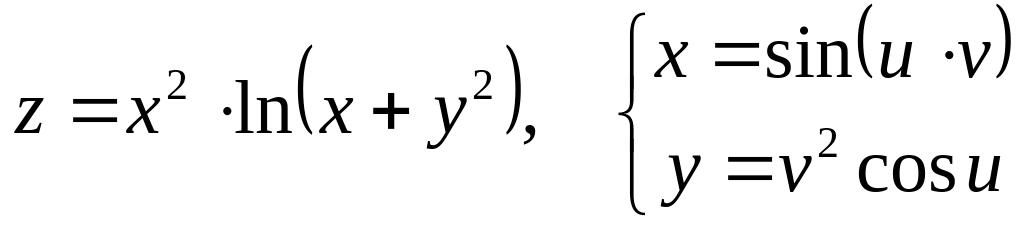
а)
 б)
б) 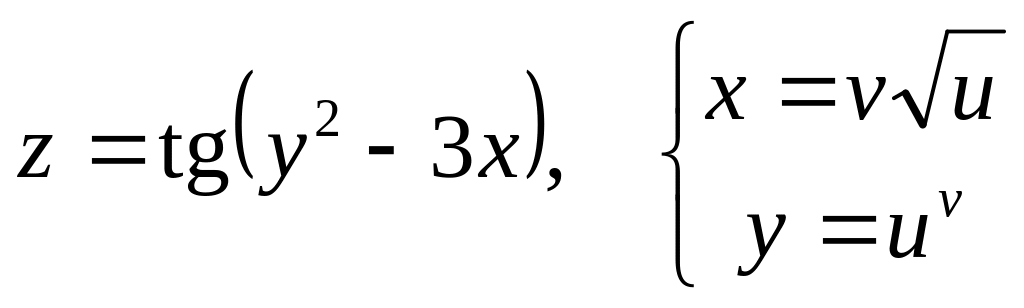
а)
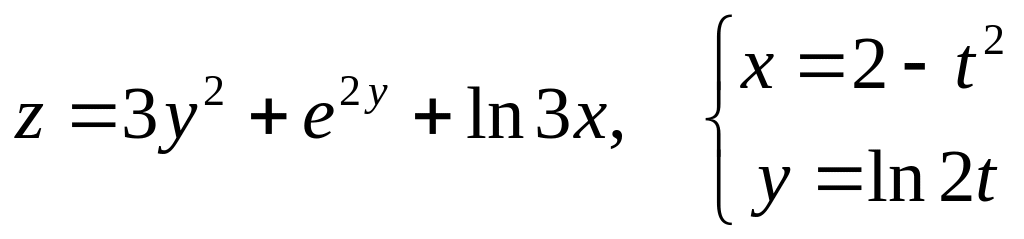 б)
б) 
а)
 б)
б) 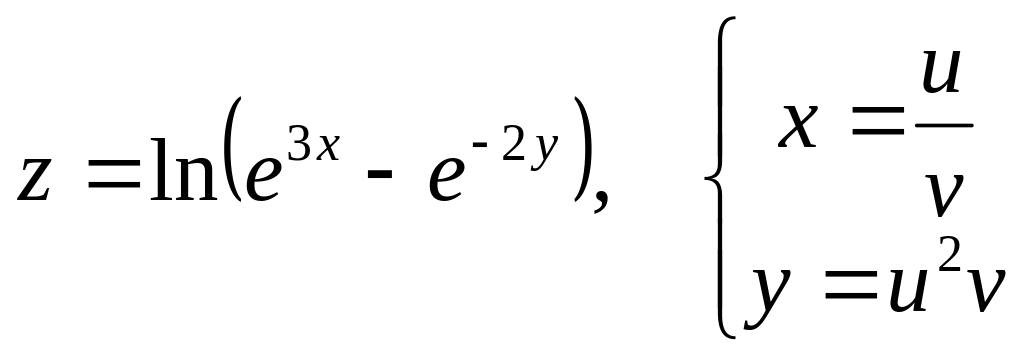
а)
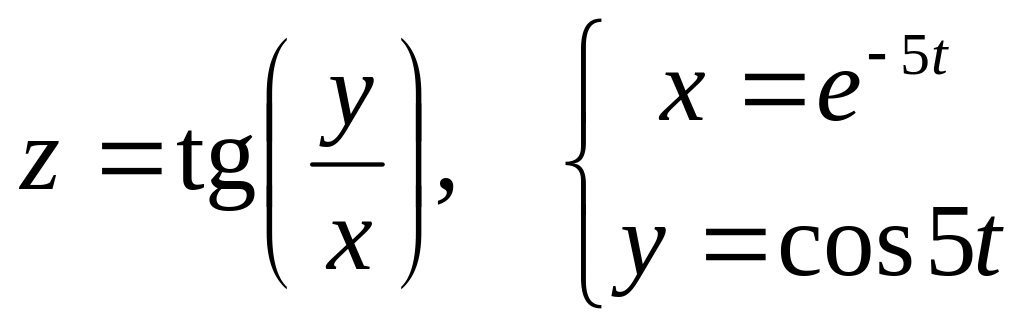 б)
б) 
а)
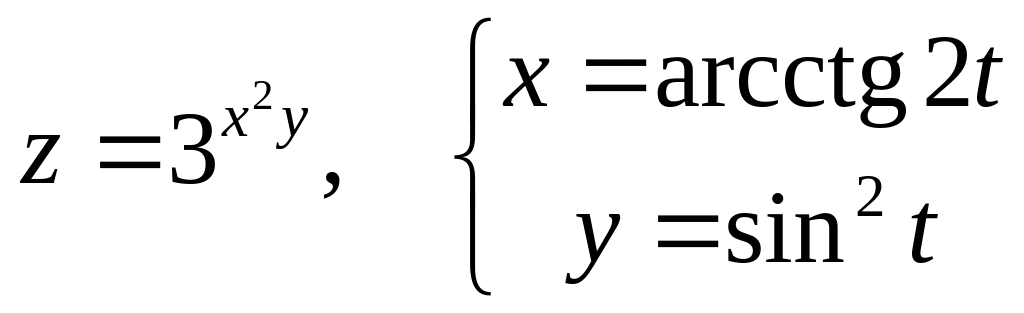 б)
б) 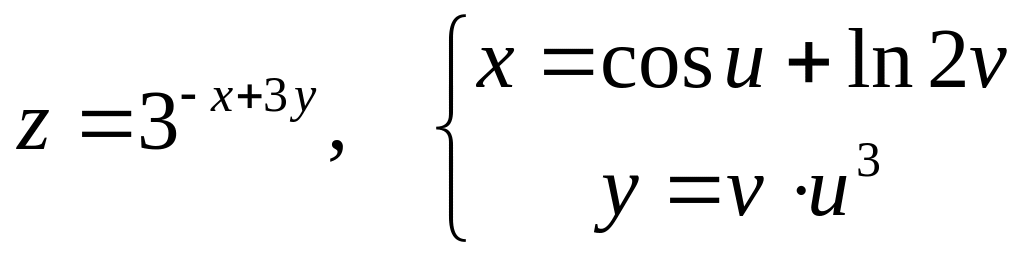
а)
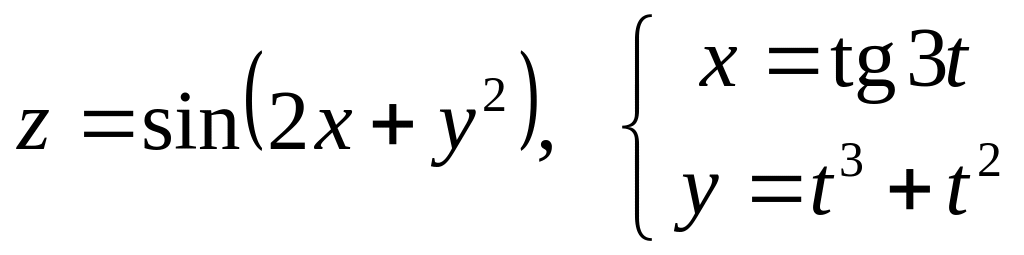 б)
б) 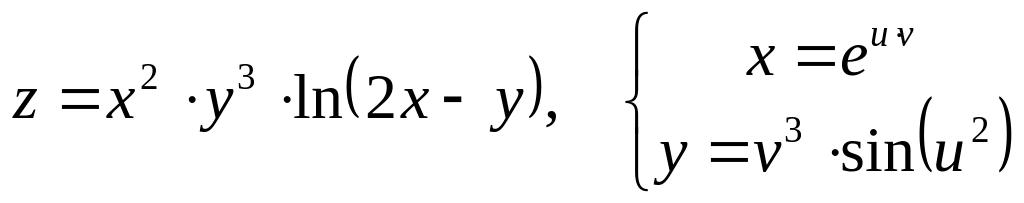
а)
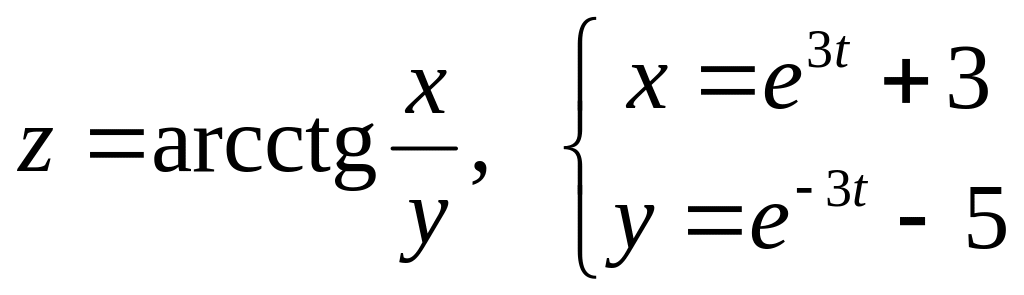 б)
б) 
З адание№5.
Показать, что данная функция удовлетворяет уравнению.
а)
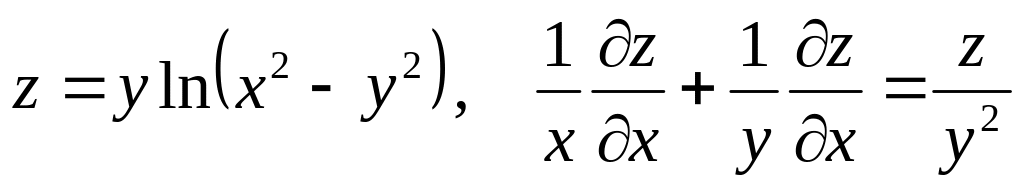
б) ![]()
а)
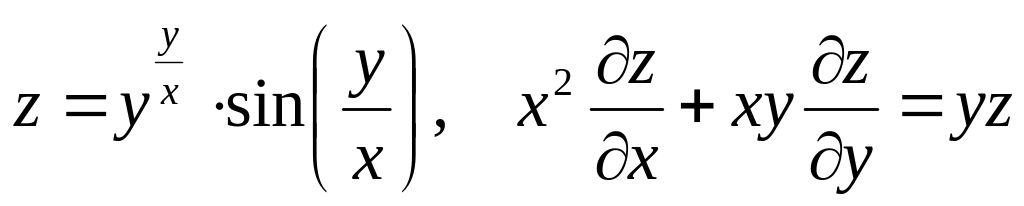
б) ![]()
а)

б) ![]()
а)

б) ![]()
а)

б) ![]()
а)
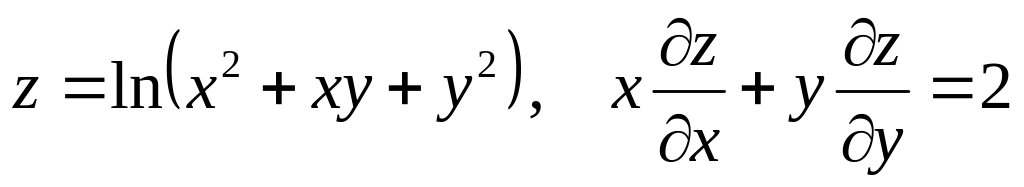
б) ![]()
а)
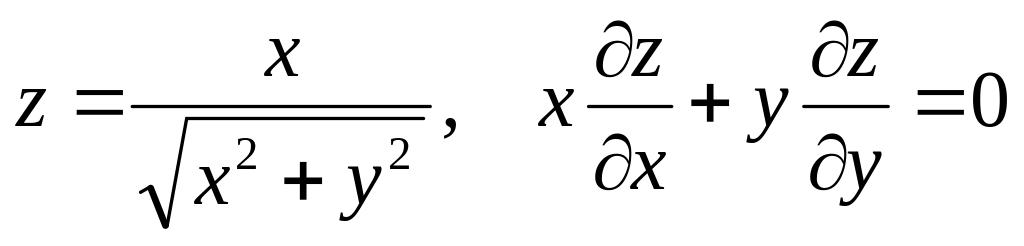
б) ![]()
а)
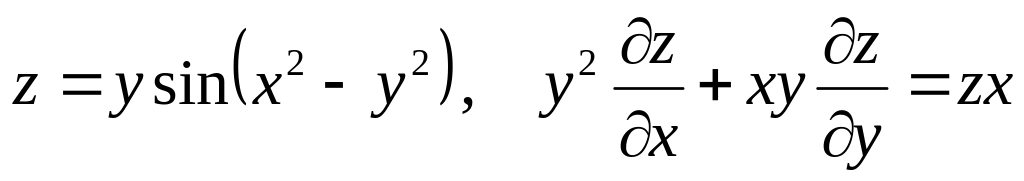
б) ![]()
а)
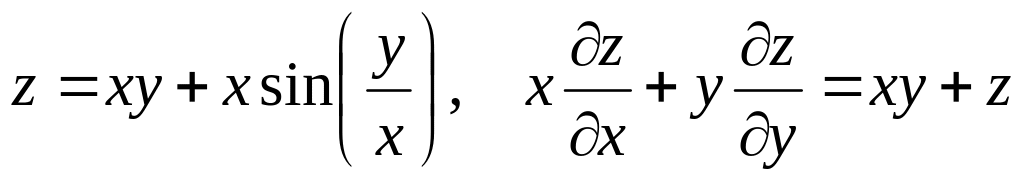
б) ![]()
а)

б) ![]()
а)
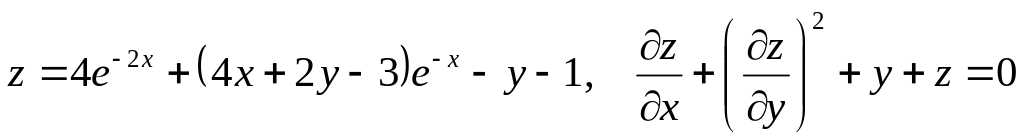
б) ![]()
а)
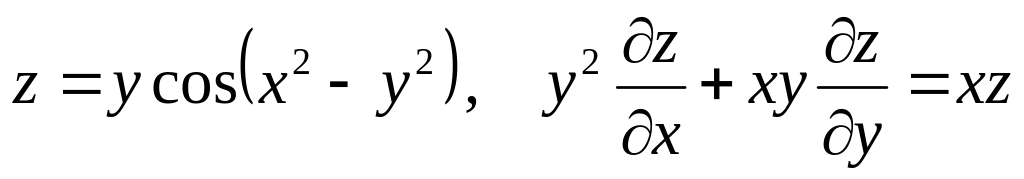
б) ![]()
а)
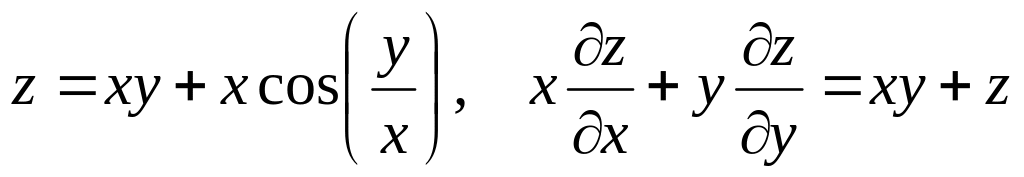
б) ![]()
а)
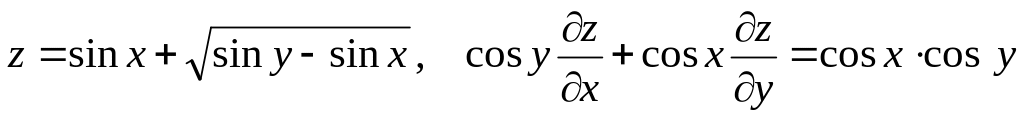
б) ![]()
а)
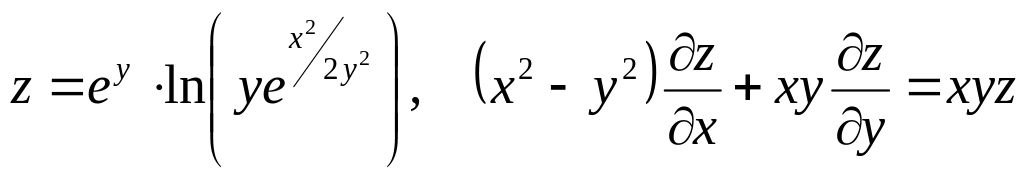
б) ![]()
а)
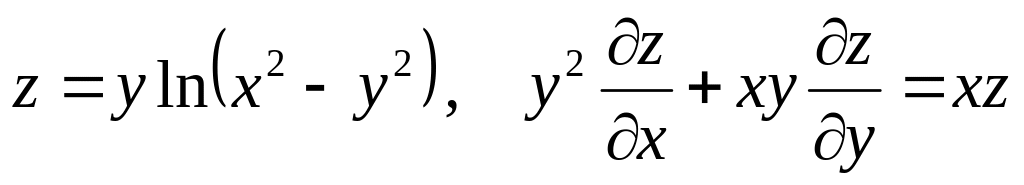
б) ![]()
а)
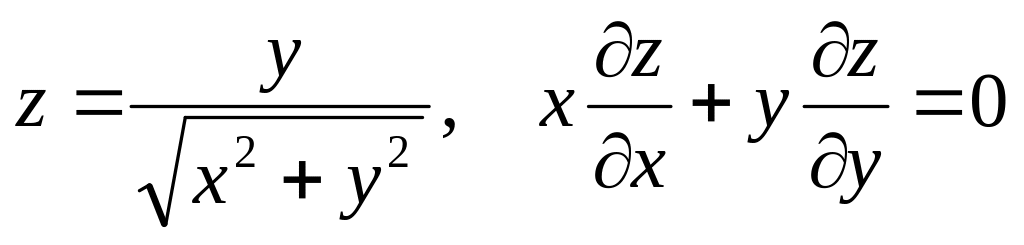
б) ![]()
а)
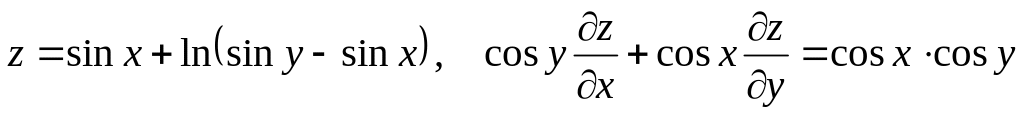
б) ![]()
а)
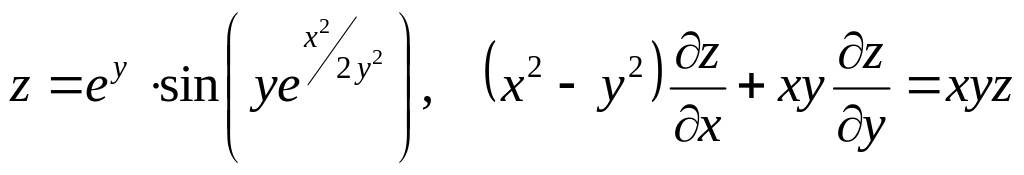
б) ![]()
а)
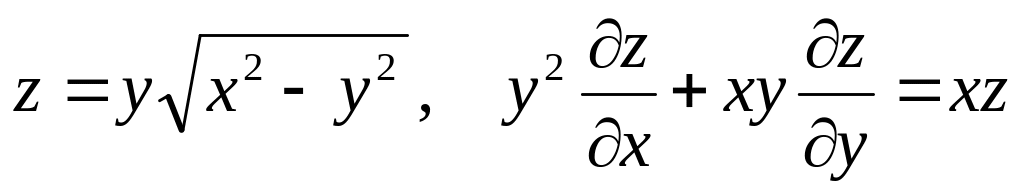
б) ![]()
а)
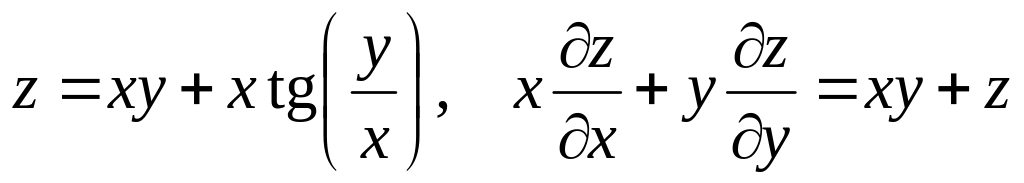
б) ![]()
а)
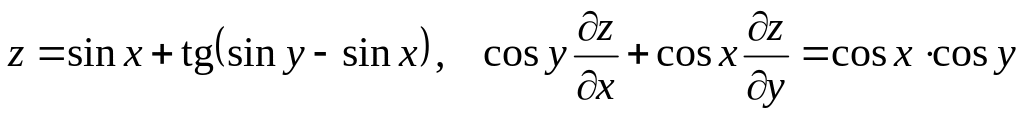
б) ![]()
а)
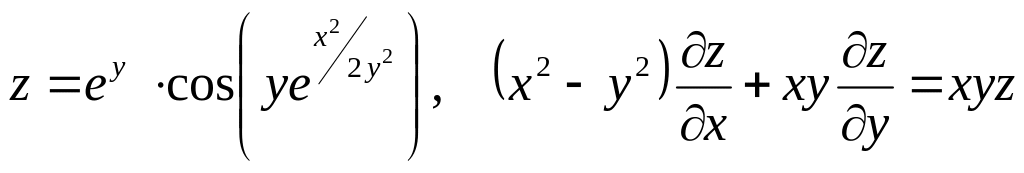
б) ![]()
а)
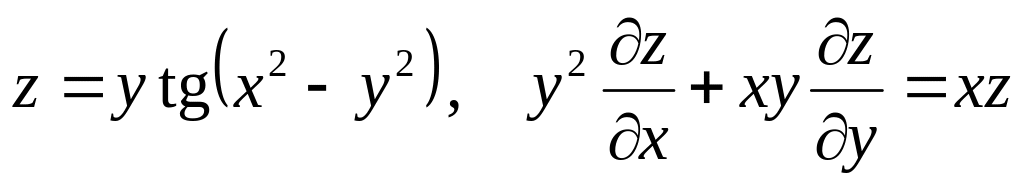
б) ![]()
а)
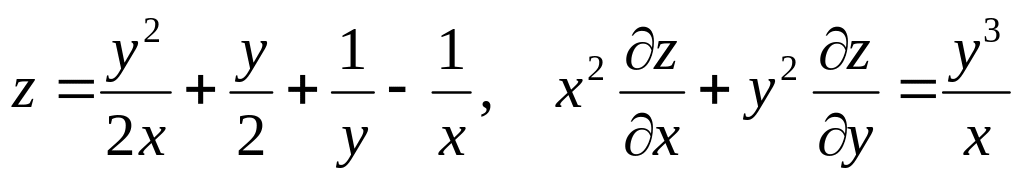
б) ![]()
а)
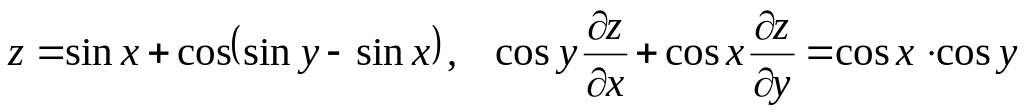
б) ![]()
а)
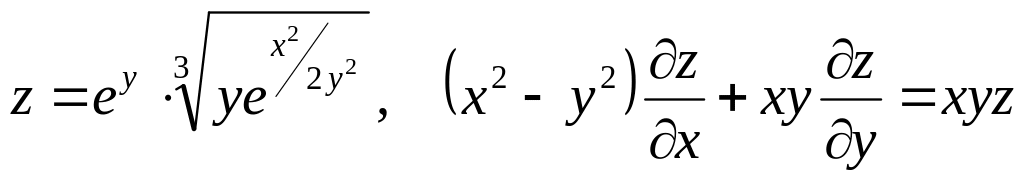
б) ![]()
а)
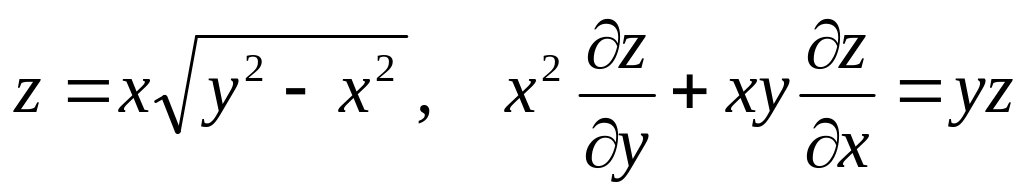
б) ![]()
а)
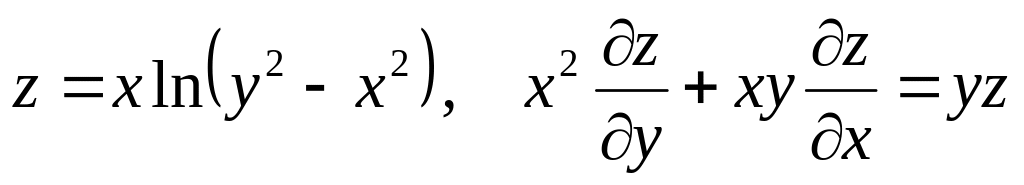
б) ![]()
а)
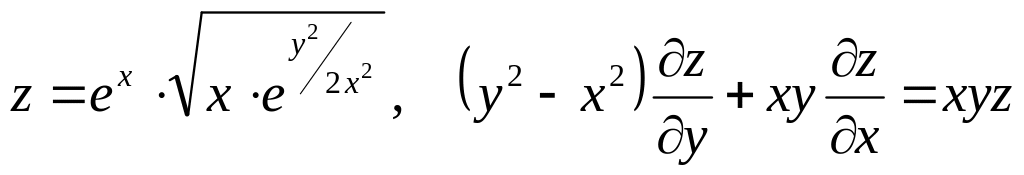
б) ![]()
Задание №6.
Найти
а)
полную производную
![]() ;
;
б)
частные производные
![]() и
и
![]()
от неявной функции заданной уравнением:
а)
 б)
б) 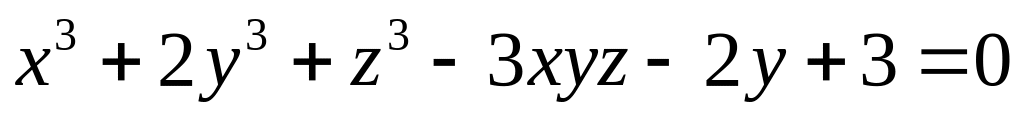
а)
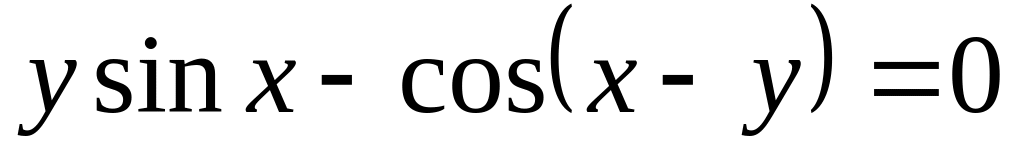 б)
б) 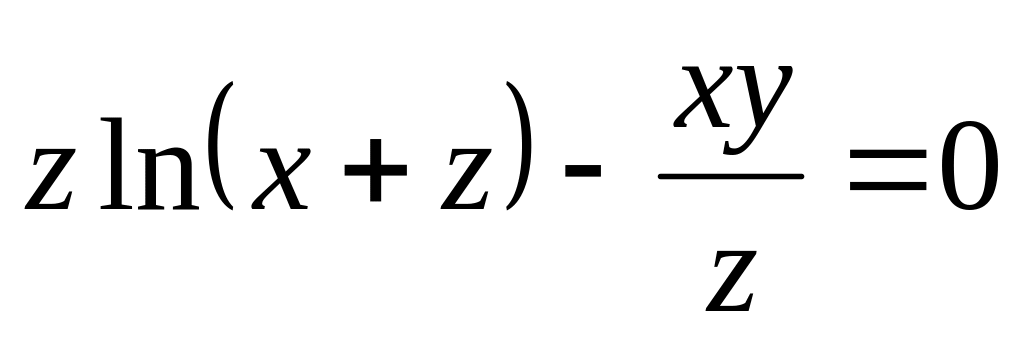
а)
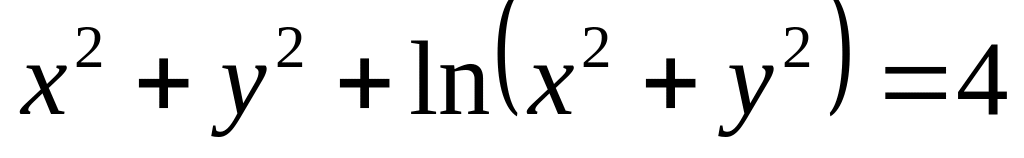 б)
б) 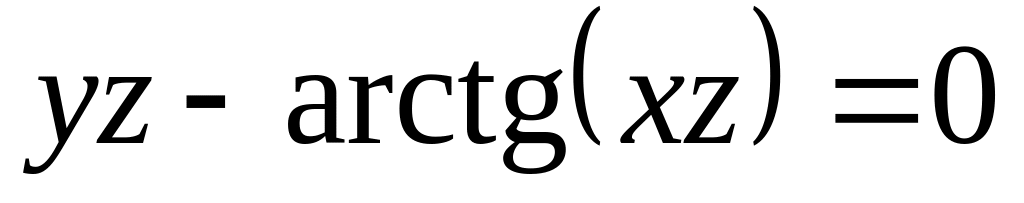
а)
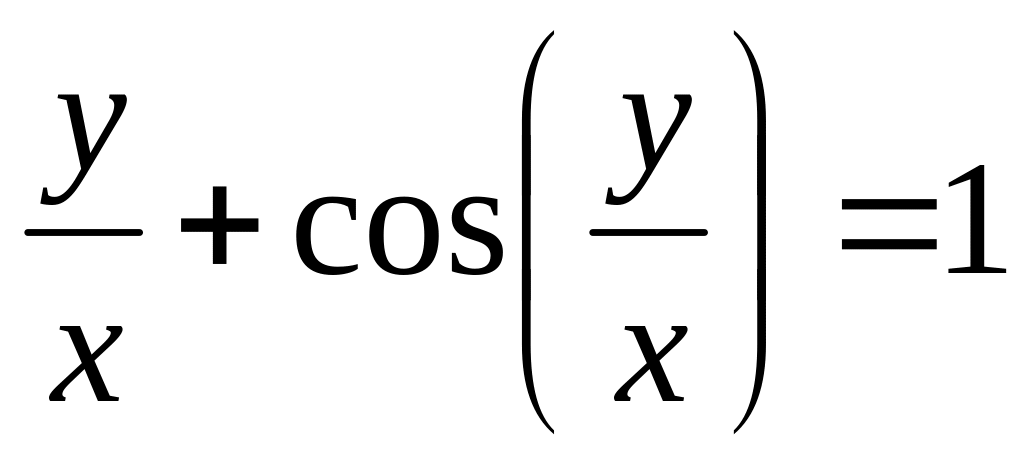 б)
б) 
а)
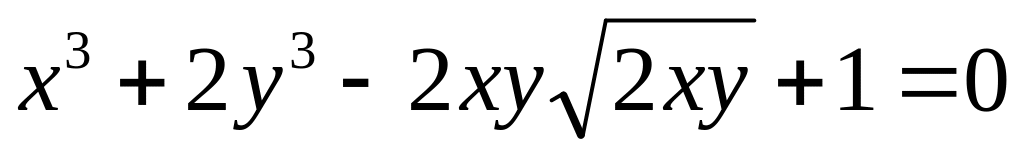 б)
б) 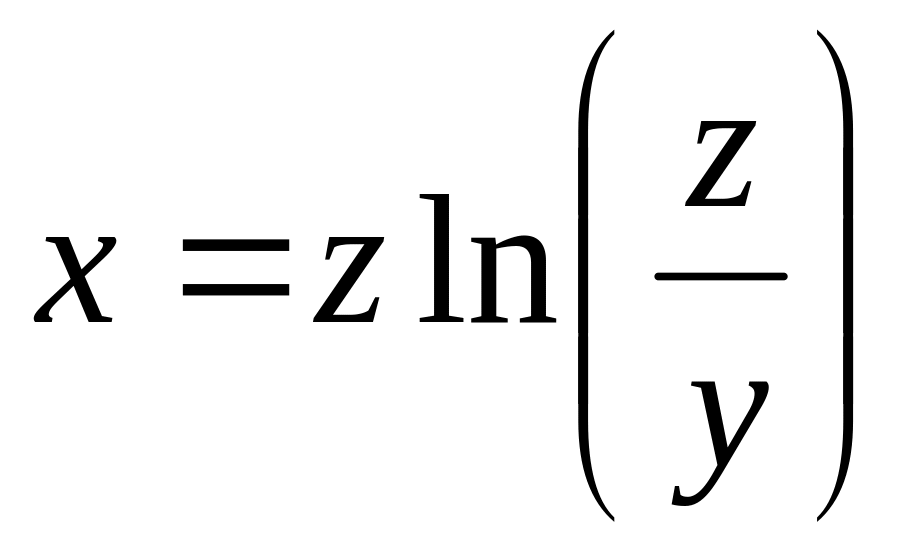
а)
 б)
б) 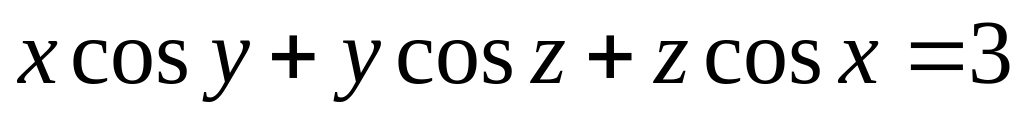
а)
 б)
б) 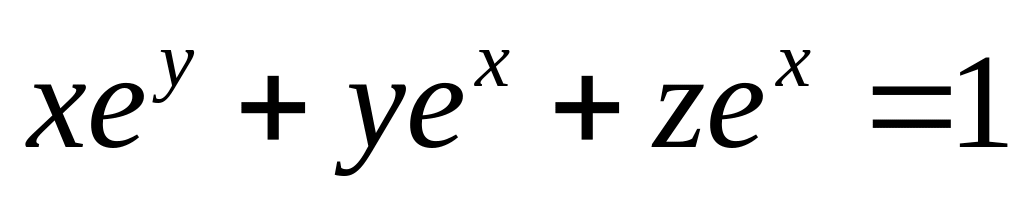
а)
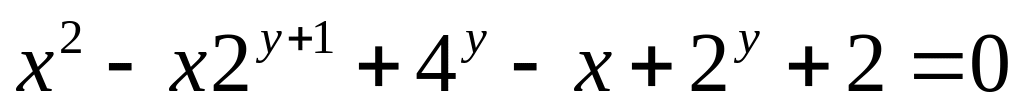 б)
б) 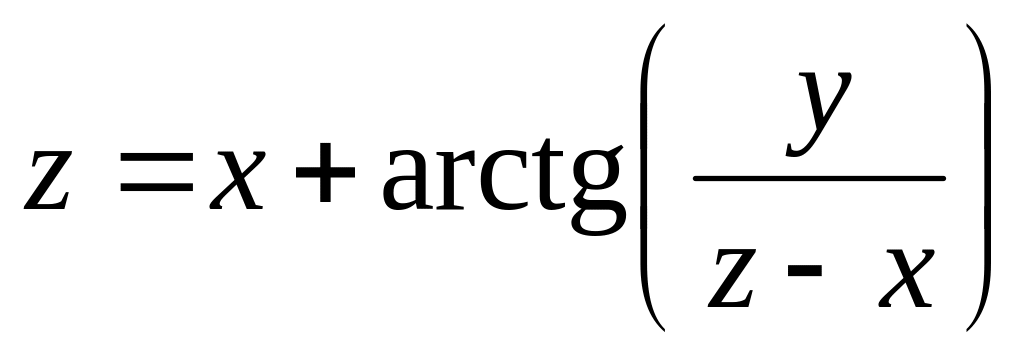
а)
 б)
б) 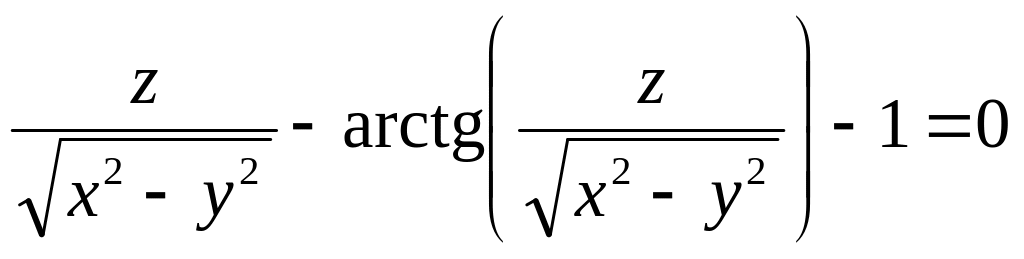
а)
 б)
б) 
а)
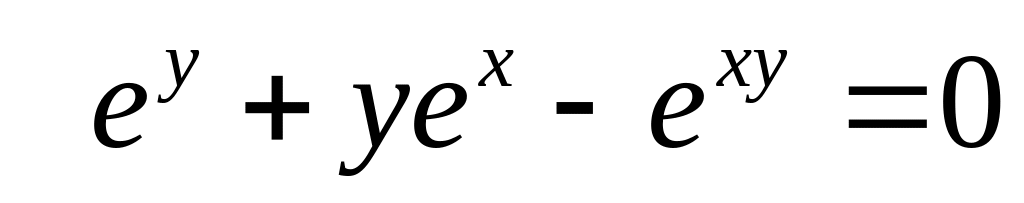 б)
б) 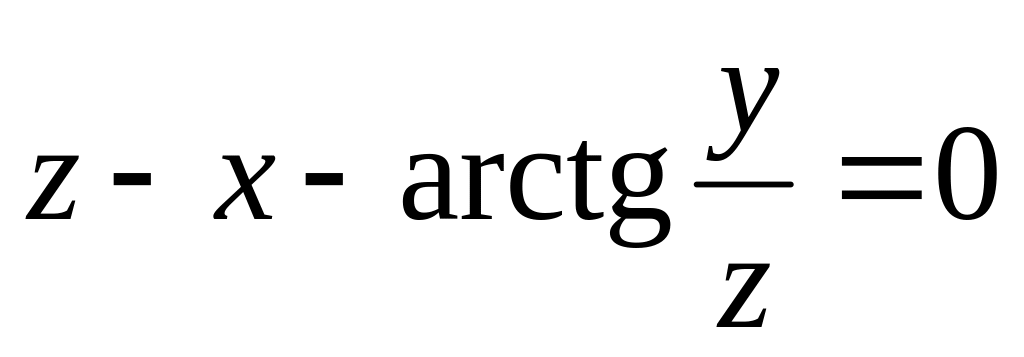
а)
 б)
б) 
а)
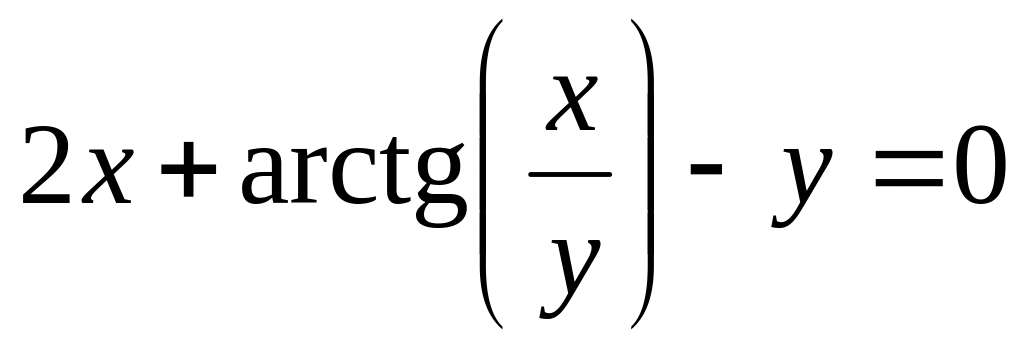 б)
б) 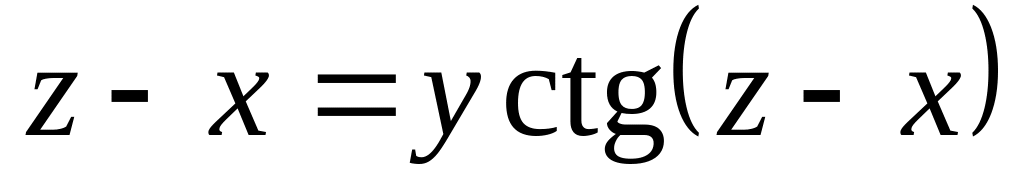
а)
 б)
б) 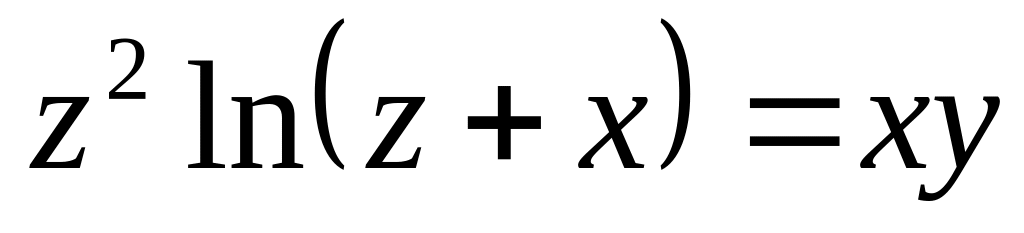
а)
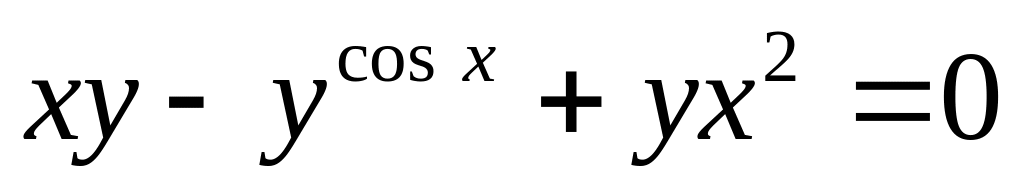 б)
б) 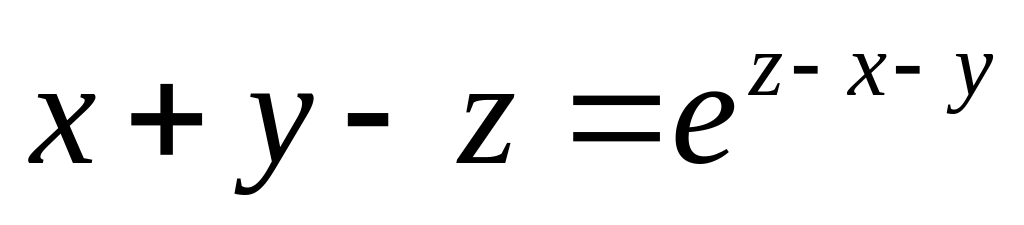
а)
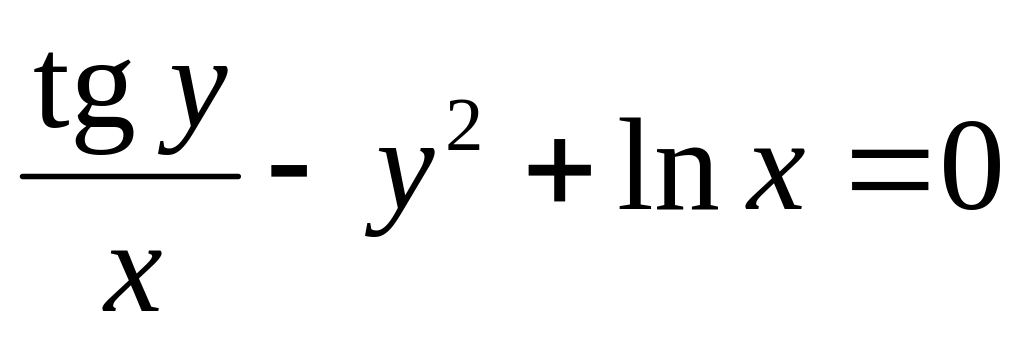 б)
б) 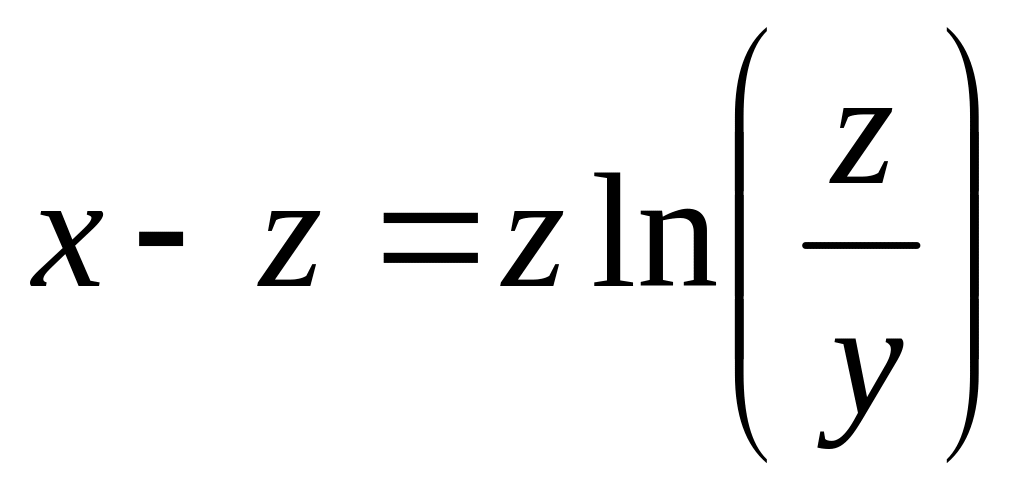
а)
 б)
б) 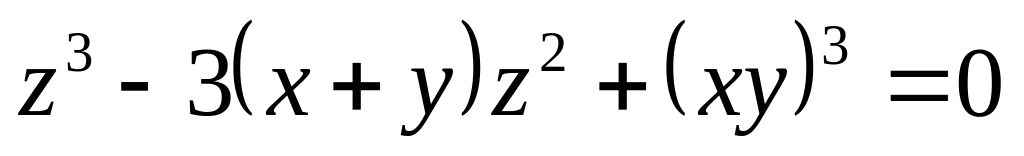
а)
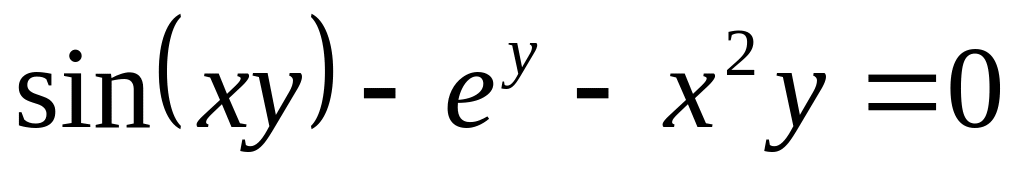 б)
б) 
а)
 б)
б) 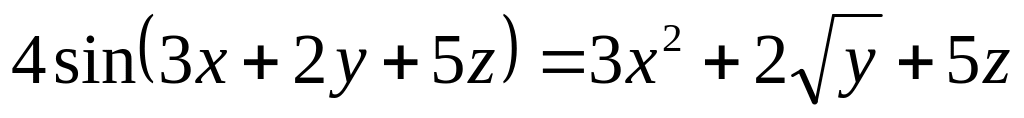
а)
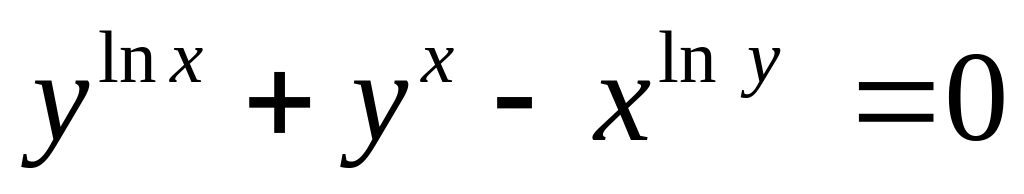 б)
б) 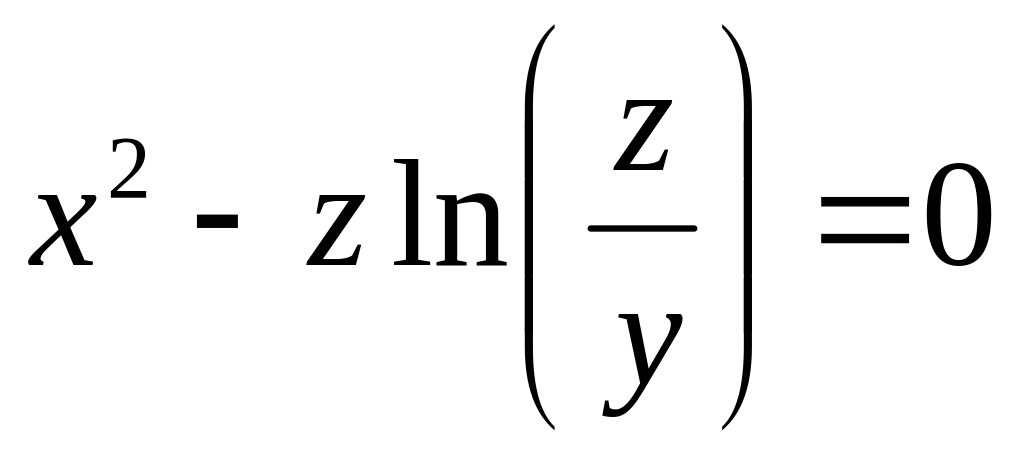
а)
 б)
б) 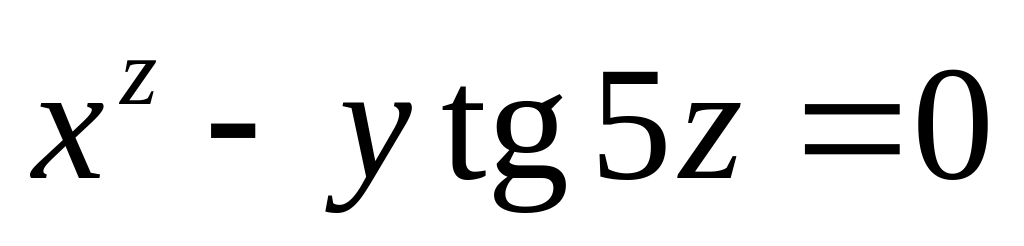
а)
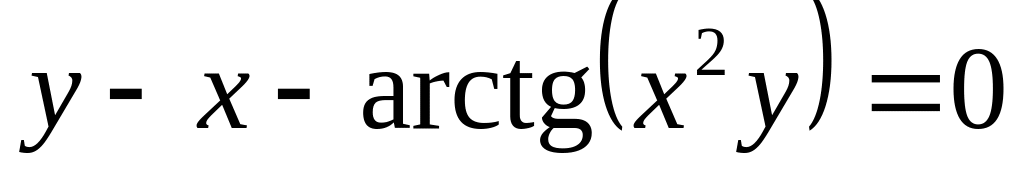 б)
б) 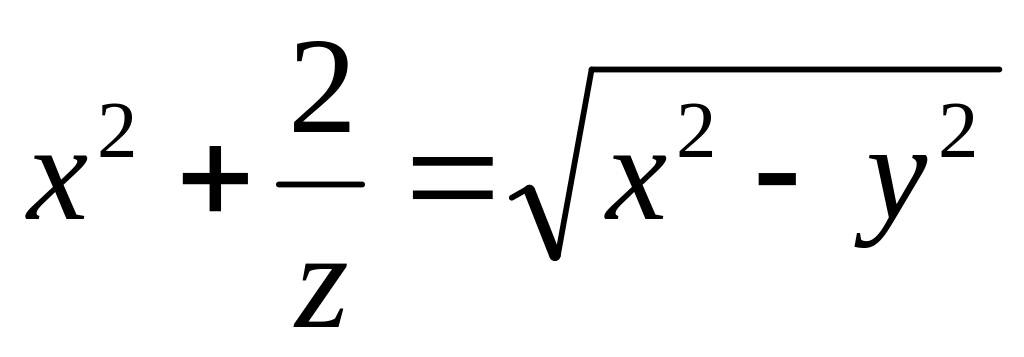
а)
 б)
б) 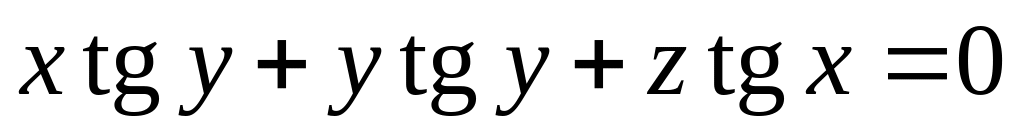
а)
 б)
б) 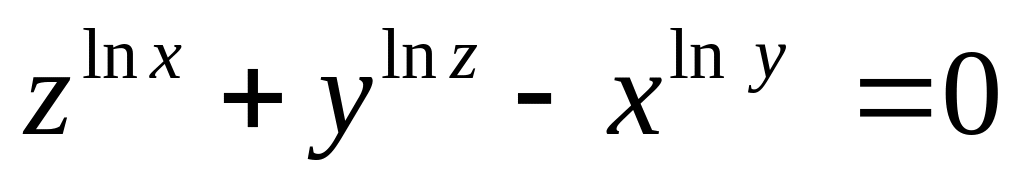
а)
 б)
б) 
а)
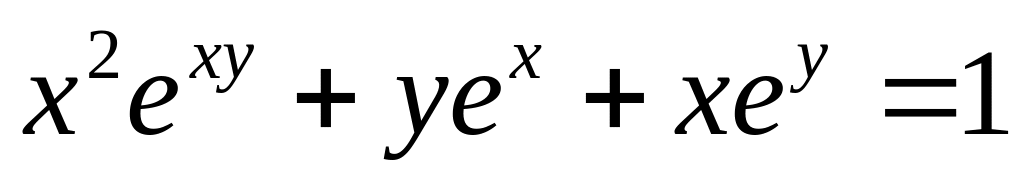 б)
б) 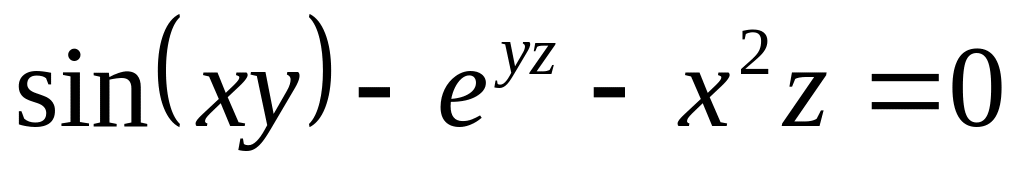
а)
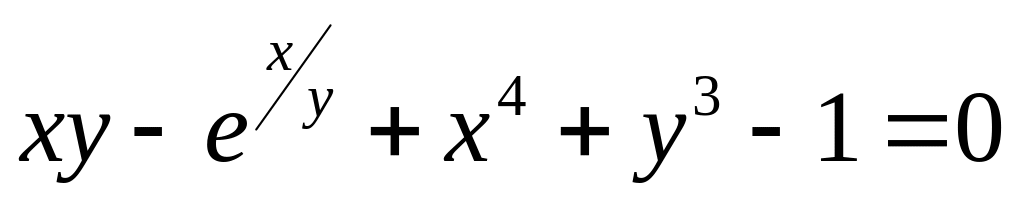 б)
б) 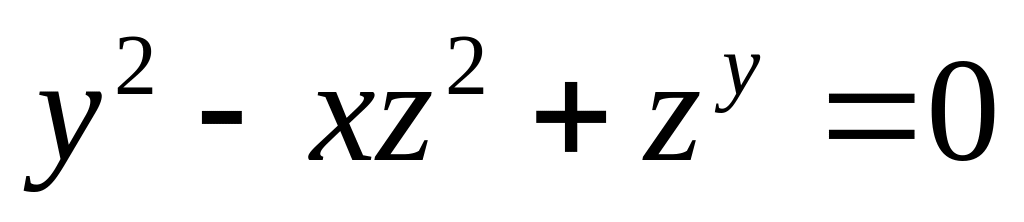
а)
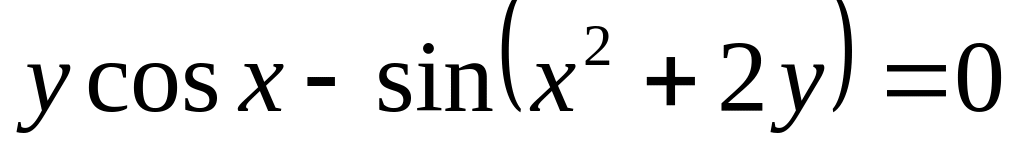 б)
б) 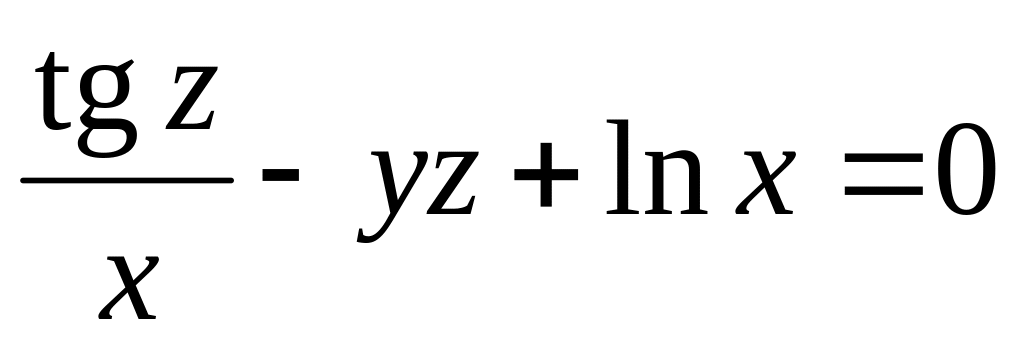
а)
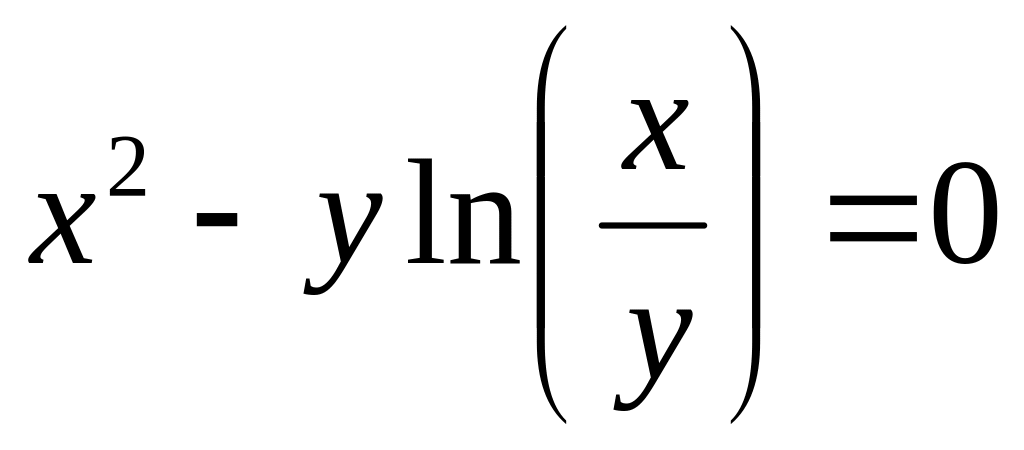 б)
б) 
а)
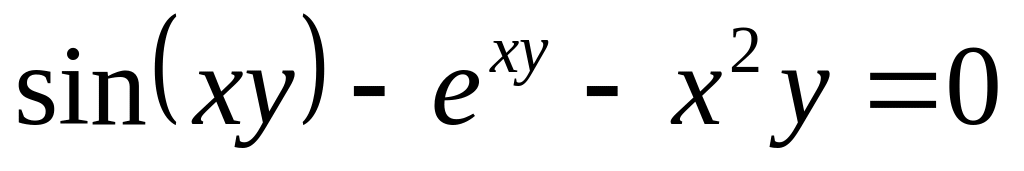 б)
б) 
Задание №7.
Найти
производную указанной функции в
направлении вектора
![]() в
точке М и градиент этой функции в точке
М.
в
точке М и градиент этой функции в точке
М.
а)
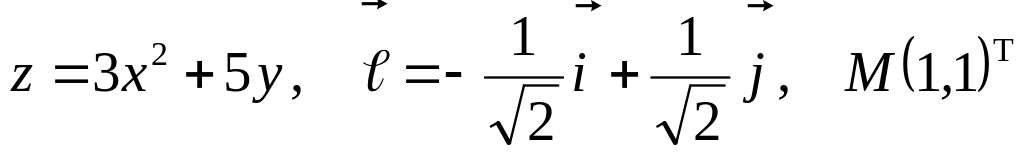
б) ![]()
а)
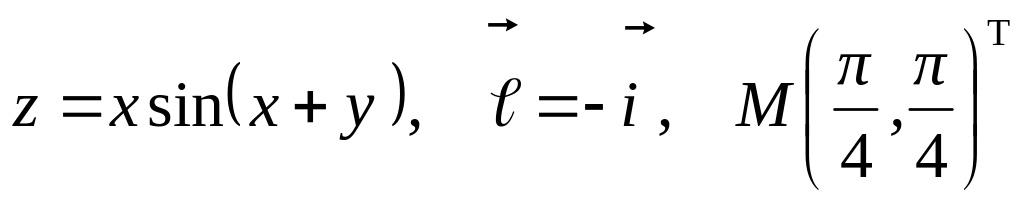
б) ![]()
а)
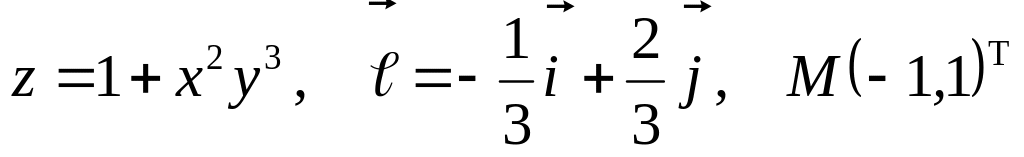
б) ![]()
а)

б) ![]()
а)
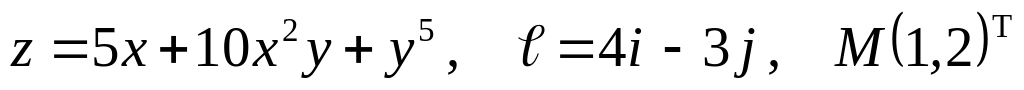
б) ![]()
а)

б) ![]()
а)
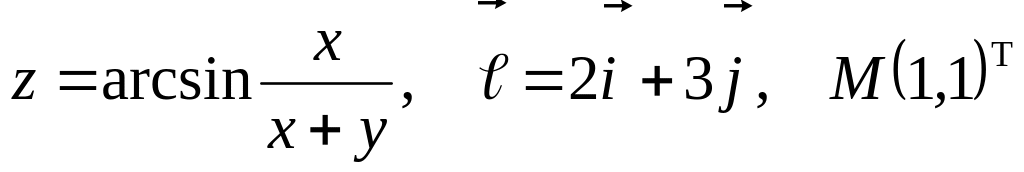
б) ![]()
а)

б) ![]()
а)
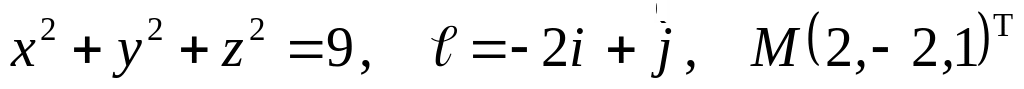
б) ![]()
а)
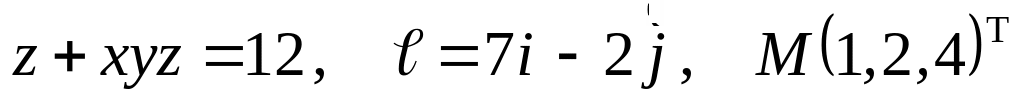
б) ![]()
а)
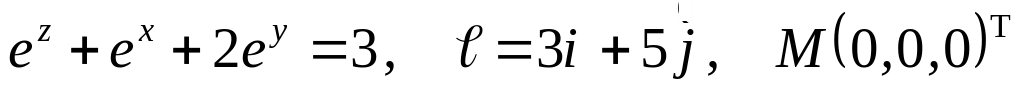
б) ![]()
а)
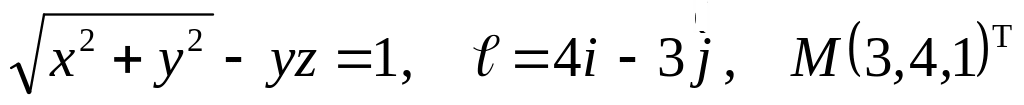
б) ![]()
а)
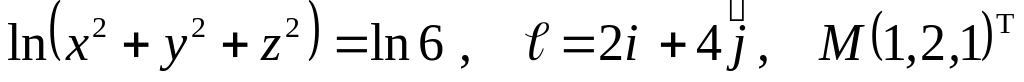
б) ![]()
а)

б) ![]()
а)
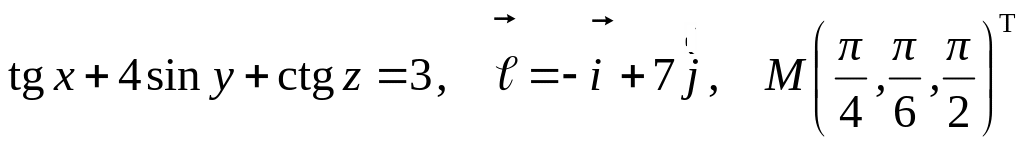
б) ![]()
а)
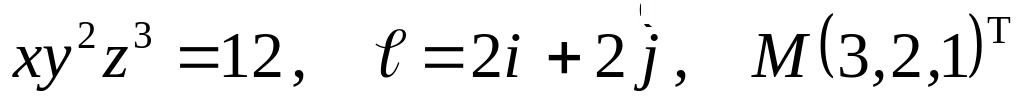
б) ![]()
а)
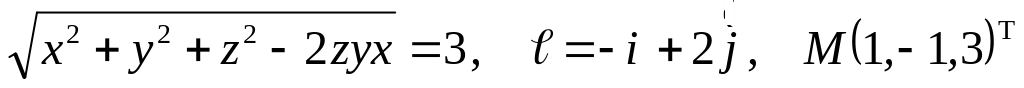
б) ![]()
а)
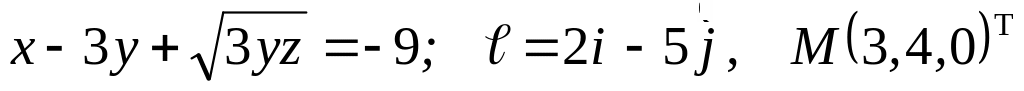
б) ![]()
а)
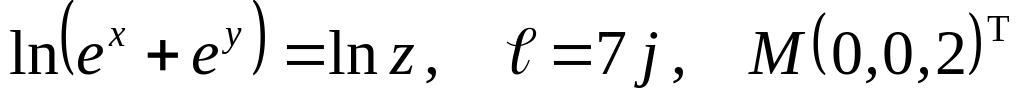
б) ![]()
а)

б) ![]()
а)
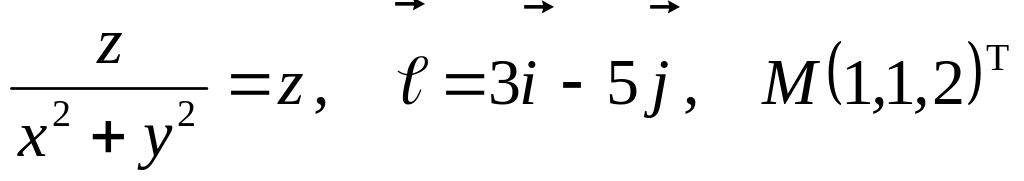
б) ![]()
а)
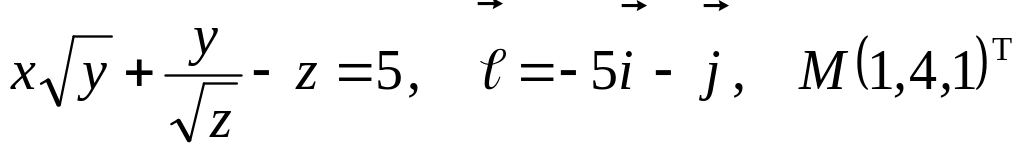
б) ![]()
а)
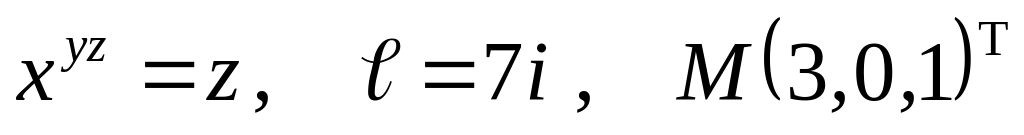
б) ![]()
а)

б) ![]()
а)
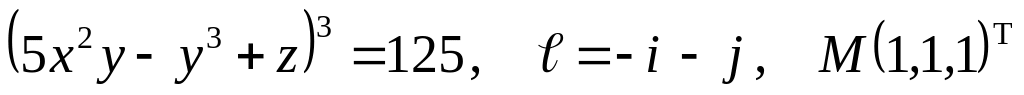
б) ![]()
а)
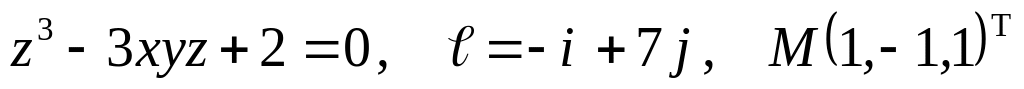
б) ![]()
а)

б) ![]()
а)

б) ![]()
а)

б) ![]()
а)
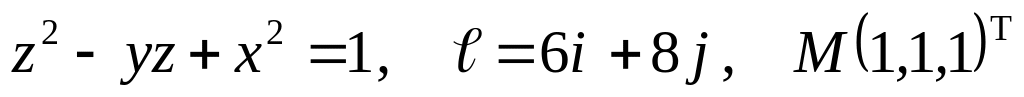
б) ![]()
Задание№8.
Написать
уравнения касательной плоскости и
нормали к поверхности S
в точке М. Линеаризовать функцию
![]() в точке М.
в точке М.
Задание№9.
Исследовать
на экстремум функцию
![]() .
.
Задание№10.
Найти
наибольшее и наименьшее значение
функции
![]() в треугольнике АВС, который задан
координатами своих вершин.
в треугольнике АВС, который задан
координатами своих вершин.
