§ 3. Производная сложной и неявной функции

Пусть – функция двух переменных и , каждая из которых является функцией независимой переменной , т.е. , .

Если – дифференцируемая в точке функция, а аргументы и – дифференцируемые функции независимой переменной , т.е. и , то производная сложной функции одной переменной вычисляется по формуле

(3.1).

Если переменная совпадает с одним из аргументов или , например , то производная сложной функции одной переменной находится по формуле

(3.2)

и называется полной производной.

Если – функция двух переменных и , а аргументы , являются функциями двух переменных , т.е. и , то функция является функцией двух переменных . Тогда её частные производные и выражаются так:

и . (3.3)

Пример 3.1. Найти полную производную , если и , .

Решение. Найдем частные производные

, , , .

Согласно формуле (3.1) получим:

.

Пример 3.2. Найти частные производные и сложной функции , если , .

Решение. Найдем частные производные

, ,

, , , .

По формулам (3.3) получим:

;

.

Пусть функция от задается неявно с помощью уравнения .Тогда производная неявной функции , где – дифференцируемая функция переменных и , вычисляется по формуле

, при условии . (3.4)

Аналогично, если неявная функция двух переменных задаётся с помощью уравнения , где – дифференцируемая функция переменных , и , то её частные производные определяются по формулам

, , при условии . (3.5)

Пример 3.3. Найти производную , если неявная функция задана уравнением .

Решение. Здесь .

Найдем , .

Тогда получим .

Пример 3.4. Найти частные производные и , если неявная функция задана уравнением .

Решение. Здесь .

Найдем , , .

Тогда и .

§ 4. Касательная плоскость и нормаль к поверхности

Касательной плоскостью к поверхности в точке называется плоскость, проходящая через точку поверхности, если угол между этой плоскостью и секущей, проходящей через точку и любую точку поверхности, стремится к нулю, когда точка стремится к точке .

Нормалью к поверхности в точке называется прямая, проходящая через точку перпендикулярно касательной плоскости в этой точке.

Если поверхность задана явно функцией и в точке существуют конечные частные производные этой функции, то уравнение касательной плоскости имеет вид:

, (4.1)

а уравнение нормали:

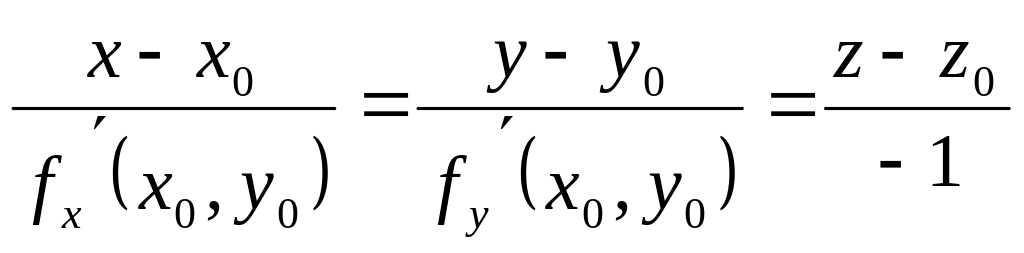. (4.2)

Если поверхность задана неявно уравнением и в точке частные производные функции конечны и не обращаются в нуль одновременно, то уравнение касательной плоскости к поверхности в этой точке записывается в виде

, (4.3)

а уравнение нормали к поверхности:

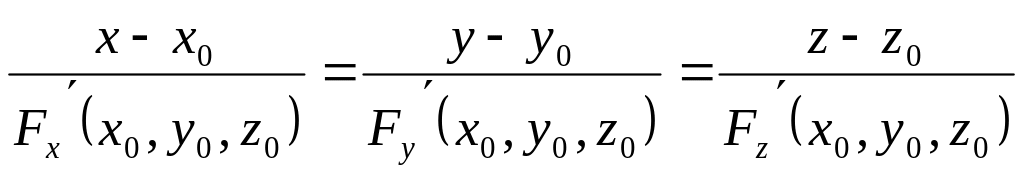. (4.4)

Пример 4.1. Написать уравнения касательной плоскости и нормали к поверхности в точке .

Решение. Вычислим частные производные функции в точке :

, .

Согласно формулам (4.1) и (4.2) получим соответственно уравнение касательной плоскости: или , и уравнение нормали: .