3. Геометрические вероятности события

Классическое определение вероятности события предполагает, что число элементарных исходов конечно. На практике же встречаются опыты, для которых множество таких исходов бесконечно.

Для преодоления недостатка классического определения вероятности, состоящего в том, что оно неприменимо к испыта­ниям с бесконечным числом исходов, введем понятие геометриче­ской вероятности события.

Пусть на плоскости задана квадрируемая область, т.е. область, имеющая площадь. Обозначим эту область буквой G, а ее площадь S_G . В области G содержится область g площади S_g (рис.1)

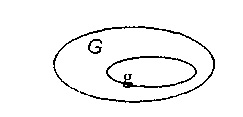
Рис. 1.

В область G наудачу брошена точка. Будем считать, что брошенная точка может попасть в некоторую часть области G с вероятностью, пропорциональной площади этой части и не зави­сящей от ее формы и расположения. Пусть А - событие, состоя­щее в том, что брошенная точка оказалась в области g, тогда гео­метрическая вероятность этого события определяется формулой

.

Аналогично вводится понятие геометрической вероятности при бросании точки в пространственную область G объема V_G, содержащую область g объема V_g:

В общем случае понятие геометрической вероятности вводится следующим образом: обозначим меру области (длину, площадь, объем) через mes g , а меру области G - через mes G (mes - первые три буквы французского слова mesure, что значит мера); обозначим буквой А событие, состоящее в том, что произошло «попадание брошенной точки в области g, которая содержится в области G». Вероятность попадания в область g точки, брошен­ной в область G, определится формулой:

.

Пример 5. В круг вписан квадрат (рис.2). В круг наудачу бросается точка. Какова вероятность того, что эта точка попадет в квадрат?

Решение. Введем обозначения: R - радиус круга, а - сторона вписанного квадрата, А - событие, состоящее в том, что точка по­пала в квадрат, S - площадь круга, S₁ - площадь вписанного квадрата. Известно, что площадь круга S = πR² . Сторона вписан­ного квадрата через радиус описанной окружности выражается

формулой , поэтому площадь квадрата S₁ = 2R² .

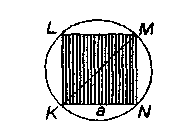
Рис. 2.

Полагая в формуле S_g= S₁, S_G = S , находим искомую вероятность .

Замечание. Выражение стороны квадрата через радиус ок­ружности можно получить следующим образом. Из треугольника KMN по теореме Пифагора будем иметь: KN² + NM² = КМ² , т.е.

a² + a²=(2R)², 2a²=4R², a² =2R², .

4. Алгебра событий

Суммой, или объединением двух событий называется собы­тие, состоящее в появлении хотя бы одного из этих событий. Сумма двух событий А и В обозначается через А + В или . Аналогично определяется и обозначается сумма n событий - со­бытие, состоящее в появлении хотя бы одного из событий. Сумму n событий А₁, А₂,...,А_n обозначают так:

или .

Произведением, или пересечением двух событий называется событие, состоящее в одновременном их появлении. Произведе­ние двух событий А и В обозначается через АВ или . Анало­гично определяется и обозначается произведение в случае n событий А₁, А₂,...,А_n обозначают: или .

Понятия суммы и произведения событий распространяются и на бесконечные последовательности событий. В этих случаях используются обозначения соответственно:

,

.

Если событие А обязательно произойдет при появлении не­которого другого события В, то говорят, что событие В представ­ляет собой частный случай события А, и пишут В  А, или Α Β (говорят также, что В влечет А).

Если В  А и Α Β , т.е. события А и В в данном опыте могут появиться или не появиться вместе, то их называют равно­сильными, или эквивалентными, пишут А= В .

Операции объединения и пересечения событий обладают некоторыми свойствами, аналогичными свойствам сложения и умножения чисел. Эти операции

коммутативны: , ;

ассоциативны:

;

;

дистрибутивны: .

Указанные свойства следуют из определения действий объ­единения и пересечения событий.

Однако не все законы сложения и умножения чисел спра­ведливы для объединения и пересечения событий. Так, для любо­го события А выполняются равенства

, .

Если U— достоверное, V— невозможное событие, А — любое случайное событие, - событие, противоположное А, то выпол­няются следующие равенства:

, или .

, или .

, или .

, или .

, или .

, или .

Из свойств операций пересечения и объединения следует, что для любых событий А и В имеем

, т.е.

, или .

Формула , или дает разложение любого события А на сумму двух непересекающихся (несовмест­ных) событий.

Если BA , то АВ = В и формула , или принимает вид:

или .

Разностью событий А и В называют событие С, которое означает, что наступает событие А и не происходит событие В. Разность событий А и В обозначается так: А-В, или А \ В.

Пример 6. Подбрасывают игральный кубик. Введем собы­тия: А - событие, состоящее в «выпадении шести очков», В - со­бытие, состоящее в «выпадении трех очков», С - событие, со­стоящее в «выпадении четного числа очков», D - событие, со­стоящее в «выпадении числа очков, кратных трем». Каковы соот­ношения между этими событиями?

Решение. Если выпало шесть очков, то тем самым выпало и четное число очков, т.е. событие А влечет событие С: А  С. Рас­суждая аналогично, получаем AD , В  D , А + B = D , C·D = A.

Пример 7. Доказать, что .

Решение. Для доказательства равенства достаточно пока­зать, что и . Если наступило событие , то это означает, что произошло событие, противоположное А+В, т.е. наступили и одновременно: . С дру­гой стороны, если произошло событие , то это означает, что произошло и , и , т.е. не наступило ни одно из событий A и В: . Итак, поскольку и , то по определению действий: .