2.3. Общие сведения о численных методах оптимизации

Теорема Вейерштрасса. Пусть в задаче условной оптимизации - компакт в , целе­вая функция непрерывна на . Тогда существует точка глобального минимума (максимума) функции на .

Замечание 1. Множество х называется замкнутым, если оно содержит все свои внутренние и граничные. Замечание 2. Множество х называется ограниченным, если

.

Иными словами, замкнутое множество можно заключить в шар радиуса c.

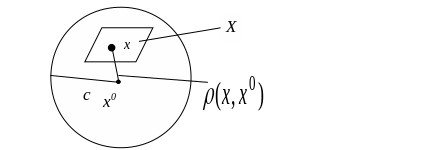
Замечание 3. Ограниченное замкнутое множество х называется компактным (компактом).

Определение 1. Численный метод - это правило (алгоритм), в соответствии с которым вычисляется последовательность точек , которая должна сходиться к реше­нию оптимизационной задачи .

Определение 2. Пусть - некоторая последователь­ность векторов из . Эта последовательность называется сходящей­ся по норме к элементу , если , т.е. если с ростом "расстояние" между элементами последовательности и вектором становится сколь угодно малым.

Правило формирования последовательности

(1)

Вектор задает направление движения в пространстве ,

число - величину "шага" при переходе из точки в точку .

1. Как выбирать векторы чтобы обеспечить движение в направлении точки ?

2. Как выбирать числа чтобы двигаться к точке достаточно (в каком-то смысле) быстро?

3. Как долго проводить вычисления по формуле (1), т.е. как узнать, что при некотором величина достаточно близка к , если неизвестно (иначе не было бы задачи)?

4. Как выбрать начальное приближение

Если используется информация только о целевой функции , алгоритм называют алгоритмом нулевого порядка; если используется информация о производных первого порядка - алгоритмом первого порядка; если используются вторые производные - алгоритмом второго порядка и т.д.

Если алгоритм за конечное число шагов приводит в точку , его называют конечношаговым, иначе - бесконечношаговым.

1. Выбор направление поиска

Определение 3. Будем говорить, что вектор в точке задает направление убывания функции (в задаче минимизации), если при всех достаточно ма­лых величинах выполняется условие . Такой вектор называют направлением убывания.

Множество всех направлений убывания функции в точке обо­значим через

Утверждение 1. Вектор тогда и только тогда, когда

(2)

2. Правило выбора параметра

(3)

Алгоритм (1) относят к методам спуска

а) ,

б) ,

в) (4)

г) (5)

(6)

Вычислительные процедуры типа (1) с (5), (6) называют алгоритмами наискорей­шего спуска

3. Скорость сходимости алгоритма

Определение 4. Пусть при . Тогда говорят:

• последовательность сходится к линейно (с линейной скоростью, со скоростью геометрической прогрессии), есл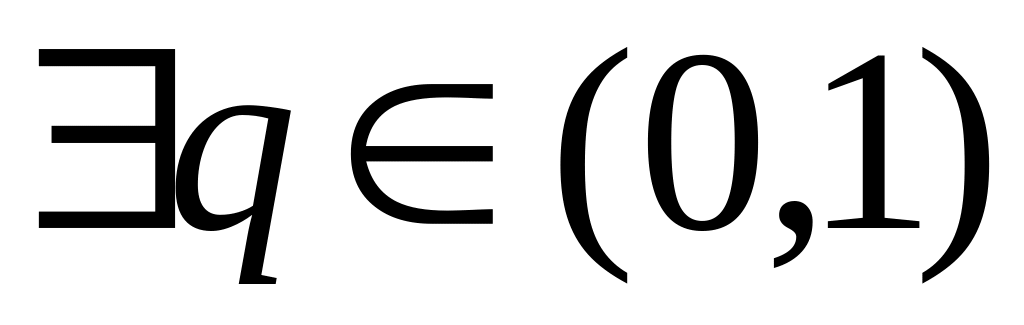и и такие, что

; (6а)

• последовательность сходится к сверхлинейно, если при такие, что

(6б);

• последовательность сходится к с квадратичной скоростью, если такие, что

(6в)