6. Пример непрерывно-дискретной модели со структурными событиями.

Рассмотрим упрощенный процесс приема данных, поступающих в реляционную базу равномерно с шагом DTNOW. В базе данных сначала заполняются единичные ячейки с общим объемом К3=150, затем ячейки половинного размера. Вся база данных имеет объем ZP=200 единиц. После ее заполнения начинается обработка всего массива поступившей информации. Необходимо определить время заполнения единичных ячеек и общее время приема данных.

Выбор концептуальной модели. В самой постановке задачи нет явных сведений о наличии функциональной зависимости между параметрами объекта исследования и временем. Поэтому возможны различные подходы к моделированию системы.

Если представить дискретную модель с событиями трех классов (приход порции данных, заполнение крупных ячеек, заполнение мелких ячеек), то неудобным обстоятельством оказывается большое количество реализаций всех событий (150 событий заполнения крупных ячеек, 100 событий заполнения ячеек половинного).

Если составить несложные уравнения процесса заполнения ячеек, а события сгруппировать в два класса по одному событию в каждом классе (окончание заполнения всех крупных ячеек, окончание заполнения всей базы данных), то общее количество реализаций окажется равным только двум. Алгоритм изменения времени прост: TNOW=TNOW+DTNOW.

Процедура SEVNT:

SUBROUTINE SEVNT

COMMON …

IF(ZP.GE.200) GOTO 2

IF(K.EQ.K3) GOTO 1

RETURN

1 I=1

CALL EVENT(I)

RETURN

2 I=2

CALL EVENT(I)

RETURN

END

Здесь первый оператор IF проверяет окончание приема всех данных, а второй - заполнение крупных ячеек (К - текущее число принятых элементарных пакетов). В зависимости от ситуации код I при вызове подпрограммы EVENT оказывается различным. Таким образом, формально на лицо два класса структурных событий: первый класс определяется условием IF(K.EQ.K3), второй - IF(ZP.GE.200).

Подпрограмма уравнений STATE:

SUBROUTINE STATE

COMMON…

IF(K.GE.K3) GOTO 1

K1=K1+1

GOTO 2

1 K1=K3

K2=K2+1

2 ZP=K1*EZP1+K2*EZP2

K=K1+K2

RETURN

END

Вначале, при К К3, растет количество заполненных единичных ячеек К1 (начальное значение К1=0). Затем идет переход по метке 2 и рассчитывается общий объем заполнения ZP (EZP1 - размер крупной, а EZP2 - размер мелкой ячеек; К2 - число ячеек половинного размера К2=0). Далее рассчитывается общее число К заполненных ячеек для последующих проверок состояния базы данных. Когда текущее К=К3, следует переход по метке 1, число К1 больше не меняется, растет количество заполненных ячеек половинного объема, что учитывается в следующем операторе для ZP.

Если второе структурное событие в рассматриваемом проимере традиционно по своему назначению (окончание имитации), то первое существенно меняет ход самой имитации, поскольку приводит к вариации К2 вместо К1. Кроме того, так как необходимые условия для возникновения этих событий (смотри процедуру SEVNT) выполняются с предельной для ЭВМ точностью, соответствующие времена TSOB должны быть приняты равными моментам TNOW, при которых выполняются указанные условия. Таким образом, уточнение TSOB не имеет смысла, и сканированиев этом случае использовано в узком плане.

Процедура поиска пронраммы реализации событий EVENT:

SUBROUTINE EVENT(J)

GOTO(1,2),J

1. CALL SOB1

RETURN

2. CALL SOB2

RETURN

END

Коды событий, передаваемые в подпрограмму (J), используются оператором перехода GOTO(1,2),J для вызова соответствующей процедуры обработки - SOB1, SOB2.

Процедура обработки событий первого класса запоминает время, соответствующее заполнению единичных ячеек:

SUBROUTINE SOB1

COMMON…

TSOB1=TNOW

RETURN

END

Значение переменной TNOW берется из общей области COMMON и заносится в память для TSOB1 (время заполнения больших ячеек).

Процедура обработки событий второго класса:

SUBROUTINE SOB2

COMMON…

TSOB2=TNOW

RETURN

END

Вызов SOB2 производится из EVENT при выполнении соответствующих условий возникновения события SOB2 в момент времени TNOW. Сказанное формально подтверждается оператором TSOB2=TNOW .

Операция запоминания текущего времени TNOW в виде момента окончания приема данных аналогична предыдущей.

Модуль управления имитацией может содержать операторы задания времени или вызов соответствующей процедуры PTNOW изменения системного времени:

SUBROUTINE SLAM

COMMON…

3. CALL INTLC

4. CALL PTNOW

IF(TNOW.GE.TSOB2) GOTO 1

CALL STATE

CALL SEVNT

GOTO 4

1. CALL OTPUTN

IF(NRNS.GE.NNRNS) GOTO 2

GOTO 3

2. CALL OTPUT

RETURN

END

После INTLC вызывается программа PTNOW для изменения системного времени. Первый оператор IF делает проверку на окончание прогона. Если прогон продолжается, в очередной раз вызывается процедура STATE, вычисляются переменные модели (время, определяющее параметры К1 и К2 в STATE, используется неявно через вызов, увеличивающий на единицу указанные переменные после очередного приращения TNOW в PTNOW; формально время в подпрограмме STATE легко трансформировать в числа К1, К2 через отношение TNOW/DTNOW). Если прогон должен быть завершен, переход по метке 1 приводит к оформлению прогонного отчета. Дальнейшая проверка вторым оператором IF показывает направление работы (к следующему прогону по метке 3 или к окончанию имитации - метка 2). Переменная NRNS в указанном операторе должна увеличиваться при каждом обращении к процедуре INTLC.

Процедура изменения времени:

SUBROUTINE PTNOW

COMMON…

TNOW=TNOW+DTNOW

RETURN

END

Алгоритм изменения системного времени прост и не предусматривает коррекции и реверса, как было выяснено выше. Это связано с тем, что два структурных события в модели возникают при достижении параметров К и ZP заданных пороговых уровней, не требующих уточнения времен TSOB1, TSOB2 (последние автоматически становятся известными при достижении К, ZP нужных величин). Шаг DTFUL и другие переменные отсутствуют, так как нет интегрирования.

Процедура INTLC содержит операторы инищиализации прогонныз переменных (в т.ч. момента начала прогона):

SUBROUTINE

COMMON…

NRNS=NRNS+1

ZP=0.

TNOW=TTBEG

K1=0

K2=0

RETURN

END

После увеличения номера прогона проводится обнуление переменных ZP, K1, K2 и задается начальное модельное время TNOW.

Главный модуль задает значения всепрогонных, а также начальное значение прогонного параметра NRNS для первого прогона:

COMMON…

NNRNS=1 (один прогон,т.к. нет случайных функций)

NRNS=0

TTBEG=0

TTFIN=900

DTNOW=2.

EZP1=1.

EZP2=.5

K3=150

CALL SLAM

STOP

END

Процедуры вывода OTPUTN и OTPUT для непрерывного моделирования не отличаются по функциям от аналогичных подпрограмм дискретных моделей.

Резюмируя вышеизложенное, можно сказать, что в зависимости от цели имитационного исследования модель может иметь разный вид и концепцию. В этом заключается один из основополагающих принципов моделирования - принцип множественности моделей. Для сложных систем отдельные ее части допустимо заменять определенными параметрами (набором параметров), упрощающими общую схему модели. Такой подход определяет принцип параметризации моделей. Далее, отсутствие сведений о характеристиках системы или ее частей делает бессмысленным само моделирование. Последнее приводит к принципу информационной достаточности. И, наконец, создаваемая модель должна обеспечить достижение цели за конечное время в условиях ограниченности ресурсов. Данный тезис говорит о принципе осуществимости моделей.

6. Стохастические системы и процессы в имитационных моделях. Вероятность. Вероятностные характеристики случайной величины. Математическое ожидание и моменты. Функции случайных величин. Выборочное среднее. Законы больших чисел. Законы распределения случайных величин.

В общем случае исследуемая система может содержать элементы, свойства которых и поведение имеют некоторую неопределенность (случайность). Исследование таких (стохастических) объектов основывается на теории вероятности и математической статистики. Стохастическим процессом называется упорядоченный временной набор случайных чисел.

Реализацией стохастического процесса является набор выборочных участков - временных рядов. Каждый прогон имитационной модели дает временные ряды изучаемых стохастических процессов.

Стохастический процесс называется стационарным, если закон поведения (распределение) случайных величин (СВ) любой его реализации не зависит от времени.

Эргодическим называется процесс, свойства которого могут быть оценены по результатам одного временного ряда.

Эксперимент. Эксперимент 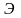является процедурой или процессом, который можно наблюдать, но результат которого нельзя точно предсказать ( в противном случае эксперимент не нужен). Множество всех полученных результатов одного и того же повторяемого стохастического эксперимента называется пространством выборок. Обработка результатов может дать новые знания (новый результат). может быть дискретным (конечным) или непрерывным.

Вероятность

Вероятность является мерой возможности. Формальной мерой вероятности является функция , которая удовлетворяет следующим аксиомам:

1. 0  ( )  1 для любого (например бросание монеты).

2. 2. ( ) = 1 для достоверного пространства (орел, решка).

3. ( 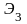  …) = ( ) + ( )+ ( ) +… для взаимоисключающих

экспериментов , , ,… ( (орелрешка) = (орел) + (решка)).

Вычисление вероятности основывается на законах теории вероятности, теории множеств, комбинаторном анализе.

Вероятностные характеристики СВ. Каждая СВ характеризуется вероятностью появления. Закон поведения (распределение) СВ также может быть вероятностным.

Вероятностное распределение представляет собой некоторое правило задания вероятности для каждого из всех возможных значений случайной переменной 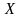. Правило задания вероятности имеет две формы в зависимости от того, является СВ дискретной или непрерывной. Дискретная СВ (ДСВ) принадлежит конечному множеству значений, непрерывная СВ (НСВ) - континууму значений.

Для дискретной СВ вероятность каждого ее значения  задается функцией вероятности ( ), принимающей для = значение

( ) = ( = ), где 0  ( )  1, ( ) = 1.

Альтернативой функции вероятности является функция распределения ( ):

( ) = (  ),

что означает вероятность того, что примет значение не больше, чем . Свойства ( ):

1. 0  ( )  1; 2) (-) = 0; 3. (+) = 1.

Функции ( ) и ( ) связаны между собой:

( ) = ( ) .

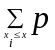Для непрерывных СВ вероятность ( ) = 0. Поэтому для них введено понятие функции плотности вероятности ( ). Функция ( ) должна удовлетворять условиям:

1) ( )  0; 2) ( ) = 1.

Функции ( ), ( ) и ( ) связаны друг с другом:

1. (   ) = ( ) ; 2) ( ) = ( ) = (  ).

Первое выражение определяет вероятность того, что на интервале СВ примет значение из этого интервала. Последнее выражение дает функцию распределения для непрерывной СВ.

Математическое ожидание и моменты. Математическим ожиданием (МО) СВ является значение, равное

[ ] = ( ) для ДСВ;

[ ] = ( ) для НСВ.

Таким образом, математическим ожиданием является взвешенная по вероятности средняя величина всех возможных значений ; -м моментом называется значение [ ], равное

[ ] = ( ) для ДСВ;

[ ] = ( ) для НСВ.

МО есть [ ] при = 1 и называется первым моментом.

Вариацией -го момента называется -й момент среднего:

.

Особое значение в теории вероятности имеет второй момент среднего, называемый дисперсией:

= .

Ковариацией случайных величин и называется величина

.

С ковариацией связан коэффициент корреляции

.

При  0 с ростом растет и . При  0 увеличение приводит к падению . Если и независимы, то график ( ) представляет собой набор случайных точек.

Функции случайных величин. Функция СВ также является СВ. Примеры:

1. ;

2. , где - константа;

3. ;

4. ;

5. ;

6. ;

7. .

Для независимых ,

.

Выборочное среднее. В математической статистике важную роль играет СВ, называемая выборочным средним (средним по выборке) , где I - размер выборки из вероятностного распределения:

= , где - одно или среднее из .

Если (I, ) = , то - функция выборки со среднеквадратичным отклонением

.

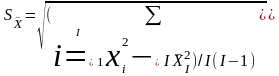Если независимы и одинаково распределены (НОР), то

= .

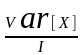Это значит, что выбрав I достаточно большим, можно уменьшить дисперсию среднего до любой малой величины.

Законы больших чисел. Поведение при увеличении размера выборки определяется двумя теоремами.

1. По мере роста величина стремится к с вероятностью, равной 1 - сильный закон больших чисел. С ним связан слабый закон больших чисел:

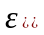= 0 для любого 0, , т.е. для любого положительного сколь угодно малого вероятность того, что модуль разности и превысит , стремится к нулю при .

2. При определенных благоприятных условиях распределение суммы (не множества) независимых наблюдений СВ стремится к нормальному, когда , независимо от характера распределения самой СВ - центральная предельная теорема.