5 Досліджуємо граф g на максимум (визначимо діаметр довжини, центр (центри) довжини і радіус довжини графа g). Для цього побудуємо матрицю відстаней.
V |
а |
b |
с |
d |
е |
f |
k |
m |
r(v) |
центри |
а |
0 |
4 |
24 |
22 |
27 |
31 |
26 |
34 |
34 |
|
b |
4 |
0 |
20 |
18 |
23 |
15 |
22 |
30 |
30 |
|
с |
24 |
20 |
0 |
24 |
17 |
30 |
25 |
33 |
33 |
|
d |
22 |
18 |
24 |
0 |
15 |
22 |
17 |
22 |
24 |
центр |
е |
27 |
23 |
17 |
15 |
0 |
15 |
20 |
7 |
27 |
|
f |
31 |
15 |
30 |
22 |
15 |
0 |
21 |
22 |
31 |
|
к |
26 |
22 |
25 |
17 |
20 |
21 |
0 |
27 |
27 |
|
m |
34 |
30 |
33 |
22 |
7 |
22 |
27 |
0 |
34 |
|
Центр довжини вершина b
R(G)=24;
D(G)==34.
6 Побудувати для графа g приклади його частини, суграфа, подграфа, зоряного графа.
Побудуємо граф, що є частиною графа G.
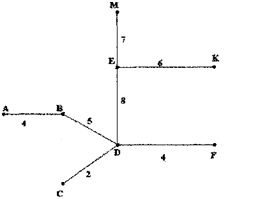
Побудуємо граф, що є суграфом графа G.
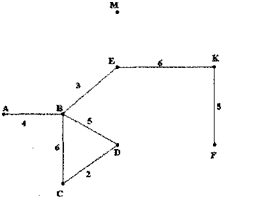
Побудуємо
граф, що є подграфом графа G на
множинівершинU(CBDE).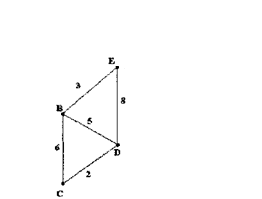
Побудуємо зоряний граф G(D).
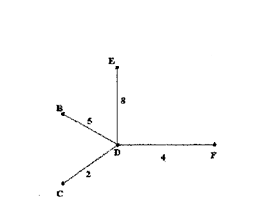
Завдання для самостійної роботи
Таблиця 4
T № |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
1 |
ab |
bс |
ad |
cd |
de |
ck |
cf |
df |
fm |
- |
km |
2 |
ab |
bc |
bd |
be |
ad |
cd |
df |
_ |
fk |
ek |
km |
3 |
ab |
ac |
ad |
bc |
cd |
cf |
ce |
ef |
fk |
em |
dm |
4 |
ab |
af |
bc |
bd |
cd |
ce |
cf |
de |
ek |
fk |
fm |
5 |
ab |
ac |
ad |
bf |
bc |
cd |
cf |
ck |
de |
km |
fk |
6 |
bc |
ab |
bd |
cf |
ck |
df |
de |
fm |
- |
cd |
km |
7 |
ас |
be |
ab |
ce |
bf |
de |
cd |
- |
dm |
ef |
fk |
8 |
bc |
ac |
ab |
bf |
df |
dm |
ce |
cd |
fk |
fm |
mn |
9 |
ab |
bc |
bd |
de |
ce |
ef |
df |
km |
fk |
ek |
- |
10 |
ab |
bc |
ad |
be |
de |
cd |
cf |
- |
fm |
ek |
km |
11 |
ab |
- |
bd |
bc |
ad |
cf |
df |
ef |
fk |
em |
km |
12 |
ab |
af |
ad |
bd |
cd |
ce |
- |
de |
fk |
dm |
fm |
13 |
ab |
bc |
bd |
cd |
ck |
de |
df |
- |
fk |
fm |
km |
14 |
bc |
be |
df |
ce |
ck |
de |
cd |
fm |
- |
km |
fk |
15 |
bd |
df |
cd |
ab |
fk |
- |
bc |
ck |
de |
fm |
km |
Продовження таблиці 4
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
16 |
ab |
ad |
bd |
be |
ec |
ef |
df |
fn |
nm |
mk |
kl |
17 |
af |
bc |
cd |
de |
dk |
kl |
mk |
fm |
fe |
be |
mn |
18 |
ab |
al |
bc |
cd |
fe |
fm |
me |
fl |
mk |
kd |
lk |
19 |
ak |
ab |
bk |
bf |
fe |
ed |
db |
cd |
cb |
- |
dl |
20 |
ad |
- |
ab |
ac |
bc |
cd |
cl |
ce |
de |
fe |
lm |
21 |
ab |
bc |
- |
ce |
cd |
df |
dm |
mf |
ml |
lf |
fe |
22 |
ab |
bc |
bd |
be |
- |
fk |
ek |
fm |
ad |
cf |
df |
23 |
ab |
ac |
ad |
bc |
cd |
ce |
cf |
de |
ek |
fk |
fm |
24 |
ab |
af |
bc |
bd |
cd |
cf |
ce |
ef |
fk |
em |
dm |
25 |
ab |
ac |
ad |
bf |
bc |
df |
de |
fm |
- |
cd |
km |
26 |
bc |
ab |
bd |
cf |
ck |
cd |
cf |
ck |
de |
km |
fk |
27 |
ac |
be |
ab |
ce |
bf |
dm |
ce |
cd |
fk |
fm |
mn |
28 |
bc |
ac |
ab |
bf |
df |
de |
cd |
- |
dm |
ef |
fk |
29 |
ab |
bc |
bd |
de |
ce |
cd |
cf |
- |
fm |
ek |
km |
30 |
ab |
bc |
ad |
be |
de |
ef |
df |
km |
fk |
ek |
- |
Таблиця 5
m № |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
1 |
3 |
5 |
7 |
4 |
2 |
1 |
6 |
8 |
7 |
4 |
3 |
2 |
6 |
4 |
2 |
7 |
3 |
2 |
4 |
5 |
3 |
8 |
7 |
3 |
8 |
4 |
2 |
5 |
6 |
4 |
2 |
3 |
3 |
4 |
2 |
4 |
2 |
1 |
5 |
3 |
8 |
3 |
4 |
2 |
5 |
6 |
7 |
5 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
6 |
3 |
4 |
7 |
7 |
2 |
2 |
6 |
5 |
3 |
8 |
4 |
7 |
7 |
1 |
3 |
4 |
2 |
5 |
2 |
1 |
6 |
1 |
8 |
8 |
5 |
3 |
5 |
4 |
2 |
7 |
6 |
2 |
4 |
1 |
10 |
9 |
6 |
4 |
7 |
5 |
3 |
6 |
2 |
3 |
4 |
8 |
11 |
10 |
3 |
3 |
5 |
4 |
9 |
9 |
2 |
5 |
7 |
11 |
10 |
11 |
6 |
2 |
1 |
3 |
5 |
7 |
9 |
11 |
4 |
4 |
8 |
12 |
7 |
2 |
5 |
3 |
1 |
9 |
11 |
2 |
8 |
6 |
4 |
13 |
2 |
2 |
1 |
5 |
6 |
9 |
10 |
5 |
10 |
11 |
8 |
14 |
3 |
9 |
7 |
8 |
2 |
5 |
4 |
2 |
3 |
1 |
1 |
15 |
1 |
5 |
3 |
1 |
2 |
2 |
9 |
5 |
8 |
4 |
6 |
Продовження таблиці 5
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
16 |
3 |
5 |
7 |
4 |
2 |
1 |
6 |
8 |
7 |
4 |
3 |
17 |
6 |
4 |
2 |
7 |
3 |
2 |
4 |
5 |
3 |
8 |
7 |
18 |
8 |
4 |
2 |
5 |
6 |
4 |
2 |
3 |
3 |
4 |
2 |
19 |
2 |
1 |
5 |
3 |
8 |
3 |
4 |
2 |
5 |
6 |
7 |
20 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
21 |
3 |
4 |
7 |
7 |
2 |
2 |
6 |
5 |
3 |
8 |
4 |
22 |
7 |
1 |
3 |
4 |
2 |
5 |
2 |
1 |
6 |
1 |
8 |
23 |
5 |
3 |
5 |
4 |
2 |
7 |
6 |
2 |
4 |
1 |
10 |
24 |
6 |
4 |
7 |
5 |
3 |
6 |
2 |
3 |
4 |
8 |
11 |
25 |
3 |
3 |
5 |
4 |
9 |
9 |
2 |
5 |
7 |
11 |
10 |
26 |
6 |
2 |
1 |
3 |
5 |
7 |
9 |
11 |
4 |
4 |
8 |
27 |
7 |
2 |
5 |
3 |
1 |
9 |
11 |
2 |
8 |
6 |
4 |
28 |
2 |
2 |
1 |
5 |
6 |
9 |
10 |
5 |
10 |
11 |
8 |
29 |
3 |
9 |
7 |
8 |
2 |
5 |
4 |
2 |
3 |
1 |
1 |
30 |
1 |
5 |
3 |
1 |
2 |
2 |
9 |
5 |
8 |
4 |
6 |
Тема: Побудова кінцевого автомата- розпізнавача для
заданої регулярної множини.
Ціль роботи: - вироблення навичок побудови та мінімізації кінцевих автоматів для розпізнання регулярної множини ланцюжків.
Приклад рішення задачі:
Побудувати МП – розпізнавач для розпізнання множини ланцюжків наступного виду : { 0(n)1(n)| n>0} (правильний ланцюжок який складається з нулів, після чого йде така ж кількість одиниць).
Рішення
Побудуємо логічну послідовність дій (алгоритм роботи) МП–автомата для розпізнання даної множини ланцюжків:
1 При обробці правильного ланцюжка першими символами, які необхідно обробити МП–автомату, буде серія із n "0". Їх кількість необхідно запам’ятати для порівняння з кількістю "1".
2 Прибуття кожного символу "0" будемо супроводжувати поданням у магазин символу А для того, щоб запам’ятати кількість нулів і порівняти потім з кількістю одиниць (у начальному стані магазин порожній).
3 Після приходу першого символа "1", нулі не повиння поступати (поступ "0" повинно переводити автомат у стан помилки "Е").
4 Поступ кожного символу "1" повинно супроводжуватися виштовхуванням з магазину символу А. Таким чином буде контролюватися рівняння кількості "0" і "1". Ланцюжок буде допускатися МП–автоматом, якщо при прибутті символу"–|" магазин буде порожнім.
Реалізуємо наведену стратегію у конкретному МП–автоматі:
1 Множина вхідних символів V = {0,1,–|}.
2 Множина магазинних символів {#,А}.
3 Множина станів S = {s1, s2}.
4 Початкова конфігурація МП–автомата – стан s1, магазин порожній( верхній символ магазину # ).
5 Допускающа конфігурація МП–автомату – стан s2, магазин порожній (верхній символ магазину # ).
6 Таблиця переходів має вид:
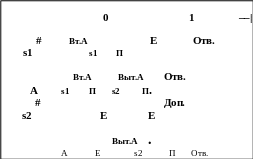
Перевіримо роботу побудованного МП–автомату. Разберемо ланцюжок 0011–| , який повинен бути допущен .
Не оброблений ланцюжок |
стан автомату |
дії з магазином |
склад магазину |
0011–| |
s1 |
– |
# |
011–| |
s1 |
Вт. А |
A# |
11–| |
s1 |
Вт. А |
AA# |
1–| |
s2 |
Выт. А |
A# |
–| |
s2 |
Выт. А |
# |
Ланцюжок допущен, тому-що кінцева конфігурація МП–автомату допускающа (стан s2, магазин порожній).