Приклад рішення задачі:

Зобразити граф G. Побудову виконати так, щоб ребра графа не перетиналися один з одним. Визначити цикломатичне число графа G, Побудувати для графа G дерево з мінімальною вагою й визначити його. Досліджувати граф G на мінімум (визначити радіус, діаметр і центр (центри) графа). Досліджувати граф G на максимум (визначити діаметр довжини, центр (центри) довжини й радіус довжини графа G). Побудувати для графа G приклади його частини, суграфа, подграфа, зоряного графа.

V = {а, b, с, d, e, f, k, m}

Е = { ab, be, bd, be, de, cd, df, fk, ek, em }

№\	1	2	3	4	5	6	7	8	9	10	11
1	ab	be	bd	be	de	cd	df	-	fk	ek	em

Вага ребер

	1	2	3	4	5	6	7	8	9	10	11
3	4	6	5	3	8	2	4	2	5	6	7

Рішення.

1 Зобразимо граф G відповідно до умови, поруч із кожним ребром зазначена його вага .

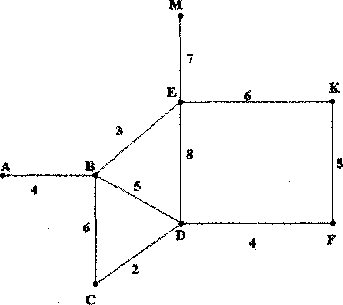
2 Визначимо цикломатичне число графа G, обчисливши його по формулі:

γ = v +m - n, де

v - число зв'язних компонентів графа,

m - число ребер,

n - число вершин.

γ = 1+10-8==3;

3 Побудуємо для графа G дерево з мінімальною вагою і визначимо її.

Будуємо ребро графа з мінімальною вагою - CD-потім на кожному кроці добудовуємо ребра з мінімальною вагою доти, поки в графі не буде утворюватися циклів.

Крок 1 - ребро CD з вагою 2.

Крок 2 - ребро BE з вагою 3.

Крок 3 - ребро АВ з вагою 4.

Крок 4 - ребро DF з вагою 4.

Крок 5 - ребро BD з вагою 5.

Крок 6 - ребро FK з вагою 5.

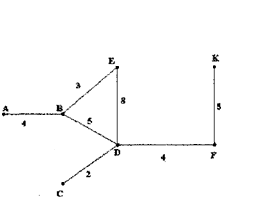
Вага дерева:

L = 2+3+4+4+5+5=23.

4 Досліджуємо граф G на мінімум (визначимо радіус, Діаметр і центр (центри) графа). Для цього побудуємо матрицю

відстаней.

V	а	b	с	d	е	f	k	m	r(v)	центри
а	0	4	10	9	7	13	13	14	14
b	4	0	6	5	3	9	9	10	10	центр
c	10	6	0	2	9	6	11	16	16
d	9	5	2	0	8	4	9	15	15
e	7	3	9	8	0	11	6	7	11
f	13	9	6	4	11	0	5	18	18
k	13	9	11	9	6	5	0	13	13
m	14	10	16	15	7	18	13	0	18

Центр вершина b

R(G)=10;

D(G)=18.