Рішення
А = ~ (q Ú ~ r) Ù р® ( q Ù~ r)
В = 7,3
С = 7,2,4
D = 7,6,5,2
1. Побудуємо таблицю істинності для висловлення а.
р |
q |
r |
~ r |
(q Ú ~ r) |
~ (q Ú ~ r) |
~ (q Ú ~ r) Ù р |
q Ù ~ r |
А |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
Спростимо висловлення А, що представимо у вигляді перемикальної схеми.
A = ~ (q Ú ~ r) Ù р® ( q Ù ~ r) =~pÚqÚ~r
П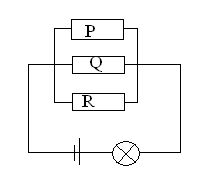
редставимо
висловлення А в виді перемикальної
схеми.
3 Використовуючи таблицю СДНФ, складемо з основних кон'юнкцій складові висловлення В, С, D й, по можливості, спростимо їх, використовуючи діаграми Венна.
В С
В = (~pÙ~qÙr) Ú (pÙ~qÙr) = r/q = r Ù~q
С = (~pÙ~qÙr) Ú (pÙqÙ~r) Ú (pÙ~qÙ~r) = (pÙ~r) Ú (~pÙ~qÙr)
D = (~pÙ~qÙr)Ú(~pÙ~qÙ~r)Ú(~pÙqÙr) Ú (pÙqÙ~r) = (qÙ~r) Ú (~pÙ r)
Побудуємо таблиці істинності для висловлень В, С і D.
р |
q |
r |
~p |
~q |
Ù~r |
в |
pÙ~r |
~pÙ~qÙr |
с |
qÙ~r |
~pÙr |
D |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
I |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |