Розрахунок постійних періодичних виплат. Функція пплат

Функція обчислює величину виплати за один період на основі фіксованих періодичних виплат і постійної процентної ставки. Виплати, розраховані функцією ППЛАТ, включають основні платежі і платежі по процентах. Синтаксис: ППЛАТ(норма; кпер; нз; бс; тип).

Типові задачі:

1. Відома майбутня вартість фіксованих періодичних виплат, що здійснюються на початку або в кінці кожного розрахункового періоду. Потрібно розрахувати розмір цих виплат.

Формула: =ППЛАТ(норма; кпер;; бс; тип).

2. Розрахувати фіксовані періодичні платежі по позиці величиною нз, необхідні для повного погашення иієі позики через кпер кількість періодів. Теперішня вартість цих виплат повинна дорівнювати теперішній сумі позики. Формула: =ППЛАТ(норма; кпер; нз; тип).

Найчастіше погашенні відбувасться в кінці кожного розрахункового періоду, тоді: Формула: =ППЛАТ(норма; кпер; нз), якщо позика погашається не повністю, тобто її майбутнє значення не дорівнює 0, то потрібно вказати аргумент бс, який буде дорівнювати непогашеному залишку позики після всіх виплат.

Приклади.

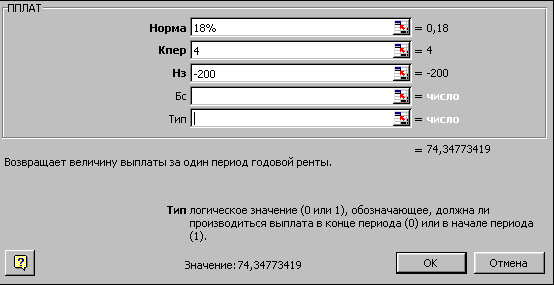
Задача 1. Необхідно нагромадити 4000 тис. грн. за 3 роки, відкладаючи постійну суму в кінці кожного місяця. Якою повинна бути ця сума, якщо норма процента по внеску становить 12% річних.

Розв'язування.

Аргументи: кпер = 3*12, норма = 12%/12, бс=4000, тип = 0 (рис.1.13).

Результат: =ППЛАТ(12%/12;12*3;;4000) = -92,86 тис. грн.

Задача 2. Банк видав позику 200 мли. грн. на 4 роки під 18% річних. Позика видана на початку року, а погашення починається в кінці року однаковими платежами. Визначте розмір щорічного погашення позики.

Розв'язування. Аргументи представлені на рис.1.14. Для банку видана позика - це негативна величина, а обчислені щорічні надходження - позитивні значення.

Результат: =ППЛАТ(18%; 4;-200) = 74,35 мли. грн.

Рис.1.13.

Рис.1.14.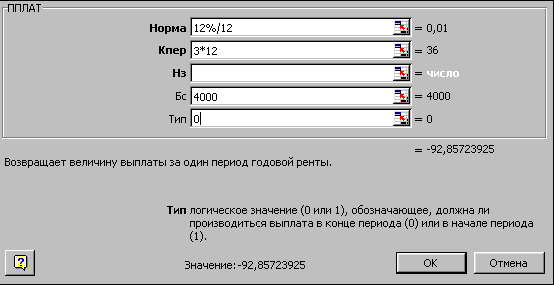

Завдання для розрахунків.

1. Визначте розмір періодичних внесків до фонду розміром 100 млн. грн., сформованого за два роки щомісячними платежами, якщо процентна ставка становить 20% річних. Відповідь:- 3422.91 тис. грн.

2. Визначте розмір щорічного погашення позики розміром 50 млн. грн., виданого на 3 роки під 38% річних. Відповідь: 30,67 млн. грн.

Розрахунок платежів по процентах. Функція плпроц

Функція обчислює платежі по процентах за заданий період на основі періодичних постійних виплат і постійної процентної ставки.

Синтаксис: ПЛПРОЦ(норма; период; кпер; тс; бс; тип).

Типові задачі:

1. Знайти розмір платежу по процентах на конкретний період, якщо погашення позики здійснюється фіксованими платежами в кінці кожного розрахункового періоду. При рівномірному погашенні позики постійна періодична виплата включає в себе платежі по процентах по непогашеній частині позики і виплату заборгованості. Оскільки непогашена частина позики зменшується по мірі її погашення, то зменшується і частка платежів по процентах у загальній сумі виплати і збільшується частка виплати заборгованості.

Формула: =ПЛПРОЦ(норма; период; кпер; тс).

2. Обчислити прибуток, який приносять постійні періодичні виплати за конкретний період. Цей прибуток являє собою суму процентів, нарахованих на накопичену (з процентами) до даного моменту сукупну величину вкладень.

Формула: =ПЛПРОЦ (норма; период; кпер;; бс; тип).

Приклади:

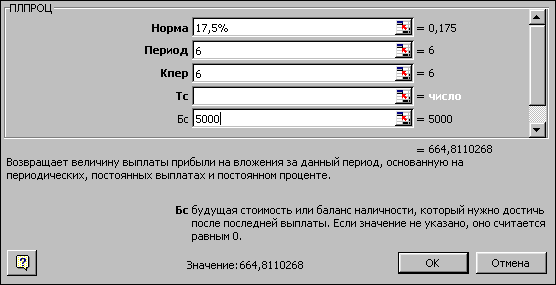
Задача 1. Обчисліть платежі по процентах за перший місяць від трирічної позики в 800 тис. грн. з розрахунку 10% річних.

Розв'язування. Аргументи функції ПЛПРОЦ для даної задачі на рис.1.15.

Результат: =ПЛПРОЦ(10%/12;1 ;12*3;800) = -6,667 тис. грн.

Рис.1.15.

Рис.1.16.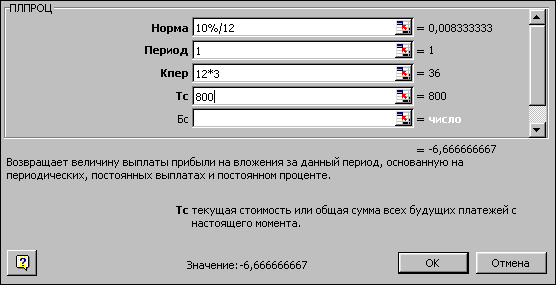

Задача 2. За рахунок щорічних відрахувань протягом 6 років був сформований фонд в 5000 тис. грн. Визначимо, який прибуток приносили вкладення власнику за останній рік, якщо річна ставка становила 17,5%.

Розв’язування: Аргументи функції представлені на рис.1.16.

Результат: =ПЛПРОЦ( 17,5%; 6;6;;5000) = 664,81 тис. грн.

Щорічно відраховувалося:

Результат: =ППЛАТ( 17,5%; 6;; 5000) = -536,27 тис. грн.

Розрахунок суми платежів по процентах по позиці. Функція ОБЩПЛАТ

Функція обчислює накопичений прибуток-(суму платежів по процентах) по позиці, яка гаситься рівними платежами в кінці або початку кожного розрахункового періоду, між двома періодами виплат.

Синтаксис: ОБЩПЛАТ(ставка; кол_пер; нз; нач_период; кон_период; тип).

Приклади.

Задача 1. Позика під нерухомість здійснена на наступних умовах: процентна ставка -9% річних; термін — 30 років, розмір позики - 125000 тис. грн., проценти нараховуються щомісяця. Знайти суму виплат по процентах за 2-й рік і за 1-й місяць позики.

Розв'язування. При введенні аргументів потрібно розібратися з початковим та кінцевим періодом. Оскільки результат знаходимо для 2-го року, а всі норми зведені до місячних, то початковим періодом буде 13-й місяць, а кінцевим періодом – 24-й місяць.

Аргументи: норма = 9%/12; кол_пер = 30*12; нз=125000; нач_период=13; кон_период=24; тип=0.

Результат: =ОБЩПЛАТ(9%/12;30*12;125000;13;24;0)=-11135,23тис.грн. Одна виплата за перший місяць складе:

Перший спосіб:

Функція: ОБЩПЛАТ. Аргументи: норма = 9%/12; кол_пер = 30*12; нз=125000; нач_период=1; кон_период=1; тип=0.

Результат: ОБЩПЛАТ(9%/12;30*12;125000;1;1;0) = -937,5 тис. грн. Другий спосіб:

Функція: ПЛПРОЦ. Аргументи: норма = 9%/12; период = 1; кпер = 30*12; нз=125000.

Результат: =ПЛПРОЦ(9%/12;1;30*12; 125000).

Розрахунок основних платежів по позиці. Функція ОСНПЛАТ

Функція обчислює величину основного платежу (виплати заборгованості) по позиці, яка гаситься рівними платежами в кінці або початку кожного розрахункового періоду, на вказаний період.

Синтаксис: ОСНПЛАТ(норма; період; кпер; тс; бс; тип).

Приклад:

Задача 1. Позика під нерухомість здійснена на наступних умовах: процентна ставка -9% річних; термін — 30 років, розмір позики - 125000 тис. грн., проценти нараховуються щомісяця. Знайти суму основних виплат по позиці за 2-й рік.

Розв'язування. Оскільки результат знаходимо для 2-го року, а всі норми зведені до місячних, то періодом буде 24 місяців.

Аргументи: норма = 9%/12; период = 24; кпер = 30*12; тс=125000; тип=0.

Результат: =ОСНПЛАТ(9%/12;12,30*12;125000;0) = -81,08 тис.грн.

Розрахунок суми основних виплат по позиці. Функція ОБШДОХОД

Функція обчислює суму основних виплат по позиці, яка гаситься рівними платежами в кінці або початку кожного розрахункового періоду, між двома періоду.

Синтаксис: ОБЩДОХОД(ставка; кол_пер; нз; нач_период; кон_период; тип).

Приклад.

Задача 1. Видана позика розміром 1000 тис.грн. терміном на 6 років під 15% річних; проценти нараховуються щоквартально. Визначити величину основних виплат за 5-й рік.

Розв’язання: Періоди з 17 по 20 складають 5-й рік. Якщо позика гаситься рівними платежами в кінці кожного розрахункового періоду, то аргументами функції будуть: ставка =15%/4; кол_пер =6*4; нз=1000; нач_период =17; кон_период =20; тип =0.

Результат: =ОБЩДОХОД (15%/4;6*4;1000;17;20;0) = 201,43 тис. грн.

Завдання для розрахунків.

1. Розрахуйте таблицю погашення позики розміром 300 млн. грн., виданої на півроку під 20% річних, якщо проценти нараховуються щомісяця. Скористайтесь функціями ППЛАТ, ПЛПРОЦ, ОСНПЛАТ. Результати представте у вигляді таблиці (рис.)