1.4.6.Система параллельных сил.

Система параллельных сил это система сил линии действия, которых, параллельны.

Если для произвольной системы параллельных сил координатные оси выбрать так, чтобы одна из осей была параллельна линиям действия сил (рис.1.4.5), тогда одно из уравнений равновесия в первой форме равновесия системы произвольных сил превратится в тождество и аналитические условия равновесия системы произвольных сил будут иметь в вид.

1. Для равновесия системы параллельных сил, необходимо и достаточно, чтобы сумма проекций всех сил на ось, параллельную силам, равнялась 0, и алгебраическая сумма моментов относительно одного центра приведения равнялась 0.

∑F_y=0

∑M_А=0

2. Для равновесия системы параллельных сил необходимо и достаточно, чтобы алгебраическая сумма моментов, всех сил, относительно двух центров приведения равнялась 0. Центры приведения не лежат на одной прямой параллельной линиям действия сил.

∑М_В =0

∑М_А =0

Для системы параллельных сил можно составить только два уравнения равновесия.

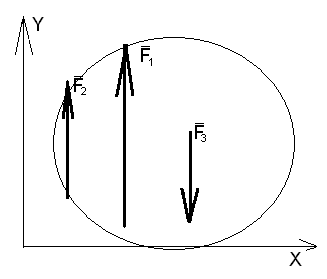
рис. 1.4.5

1.4.7 Методика решения зада

1. Отбрасываем связи, заменяем реакциями.

2. Составляем расчётную схему.

- Балку заменяем линией.

- Распределенную нагрузку заменяем сосредоточенной (смотри рис.1.4.6).

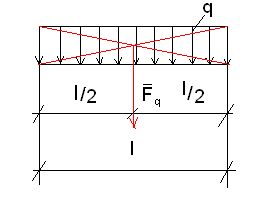
рис.1.4.6

F_q=ql

F_q прикладывается в центре.

q- интенсивность распределенной нагрузки.

l – расстояние на котором действует распределенная нагрузка.

- Все силы переносят на линию.

3. Составляем уравнения равновесия.

4. Проверка.

1.4.8 Пример

Задание.

Для балки, изображенной на рисунке 1.4.7, найти опорные реакции.

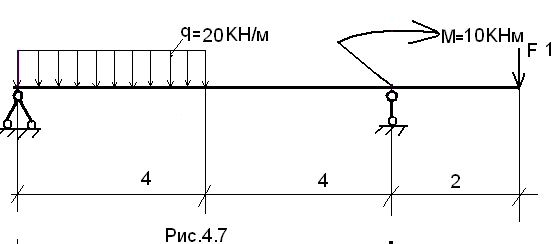
Решение.

1 Составляем расчетную схему.

- Отбрасываем связи, заменяем реакциями.

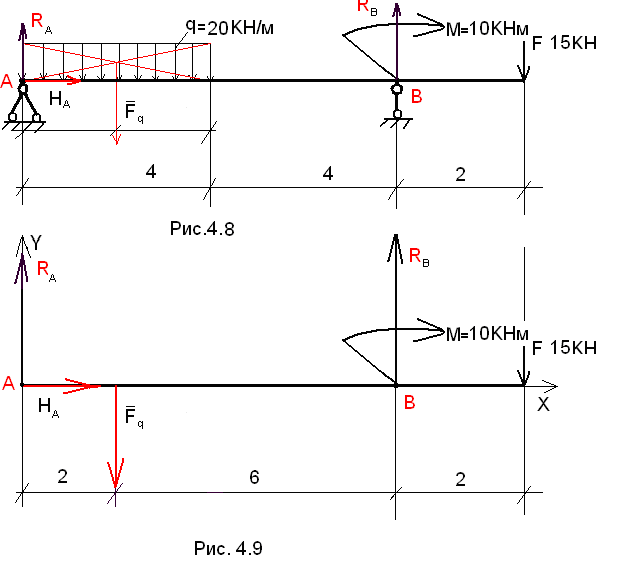
-Распределенную нагрузку заменяем сосредоточенной (рис.4.8) .

F_q=ql =20·4=80КН/м

-Балку заменим линией (рис.4.9).

-На балку в проекционной связи переносим все силовые факторы и проставляем размеры(рис.4.9).

2. Составляем уравнения равновесия.

∑F_x=0

∑М_В =0

∑М_А =0

∑F_x= Н_А= 0

∑М_В = F_q ·2+M-R_B ·8+F·10=0

∑М_А = - F_q ·6+M+R_A ·8+F·2=0

3.Решаем систему уравнений.

∑М_В = 80 ·2+10-R_B ·8+15·10=0 => R_B =(160+10+150)/8=40КН

∑М_А = - 80·6+10+R_A ·8+15·2=0 => R_А =(480-10-30)/8=55КН

4. Проверка.

∑F_Y=0

∑F_Y= - F_q +R_B -F+ R_A=0 ; -80+40-15+55=0 ;0=0

1.5 Центр тяжести плоской фигуры

При изучении темы рассмотрим следующие вопросы:

1.5.1 Центр системы параллельных сил.

1.5.2 Сила тяжести и центр тяжести тел.

1.5.3 Статический момент площади относительно ости.

1.5.5 Центр тяжести простейших фигур.

1.5.6 Методика решения задач по определению центра тяжести фигуры сложной формы.

1.5.7 Примеры решения задач.

В результате изучения темы студент должен :

Знать статические моменты плоских фигур, формулы для определения центра тяжести плоской фигуры;

уметь рассчитывать координаты центра тяжести плоской фигуры.

После изучения темы необходимо ответить на следующие вопросы:

1. Что такое центр тяжести?

2. Назовите основные методы определения центра тяжести.

3. В какой последовательности определяется центр тяжести сложной фигуры?

В пространственной системе сил рассматривается момент силы относительно оси. Момент силы относительно оси равен моменту проекции силы на плоскость перпендикулярную оси относительно точки их пересечения. Момент силы относительно оси равен нулю, если сила проходит через ось и если сила и ось лежат в одной плоскости.