3.4 Условия равновесия пар сил.
Для равновесия свободного твердого тела, находящегося под действием системы пар сил, необходимо и достаточно, чтобы алгебраическая сумма моментов всех пар была равна нулю.
1.4 Плоская система произвольных сил (пспс)
При изучении темы рассмотрим следующие вопросы:
1.4.1 Понятие « Система произвольных сил»
1.4.2 Приведение системы произвольных сил к данному центру.
1.4.3 Равнодействующая произвольной плоской системы сил.
1.4.4 Частные случаи приведения произвольной плоской системы сил
1.4. 5Условия равновесия произвольной плоской системы сил:
Геометрическое.
1.4.6.Система параллельных сил.
1.4.7 Методика решения задач.
1.4.8 Пример решения задач.
В результате изучения темы студент должен :
знать понятие момента силы относительно точки, его свойства, условия равновесия параллельной и произвольной системы сил, типы нагрузок и виды опор.
уметь определять опорные реакции балок
После изучения темы необходимо ответить на следующие вопросы:
1. Каково геометрическое условие равновесия системы произвольных сил?
2.Сколько существует форм аналитического условия равновесия системы произвольных сил?
3.Сколько существует форм аналитического условия равновесия системы
параллельных сил?
4.Какая теорема используется при решении задач?
1.4.1 Понятие « Система произвольных сил»
Плоскость системы произвольных сил – это система сил, линии действия которых, направлены произвольно.
Теорема:
Всякую силу, приложенную к твердому телу, можно переносить в любую точку тела параллельно, для того, чтобы действие сила на тело не изменилось, необходимо к телу приложить пару с моментом, равным моменту исходной силы относительно точки, в которую перенесли эту силу.
Доказательство:
Рассмотрим тело,
к которому приложена сила F
в точке B
(рис.1.4.1) .Действие этой силы на тело не
изменится, если точке B1
параллельно силе
приложить уравновешенную систему сил
и
,
при чем
=
=
В результате наших действий мы получили,
что
{ }~{ , , }
Систему трех сил представим в виде двух подсистем и , .
Система сил , представляет собой пару сил, момент которой равен моменту силы относительно точки В1, в которую эта сила переносится, а сила это сила перенесенная из точки В в точку В1 параллельно. Что нам и требовалось доказать.
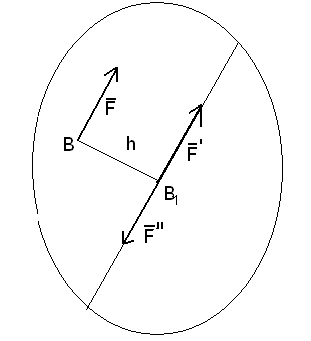
Рис.1.4.1
1.4.2 Приведение системы произвольных сил к данному центру.
Рассмотрим тело, на которое действует система сил
{ 1, 2 ,... n}, приложенных в точках В1 , В2, Вn ( рис.1.4.2).
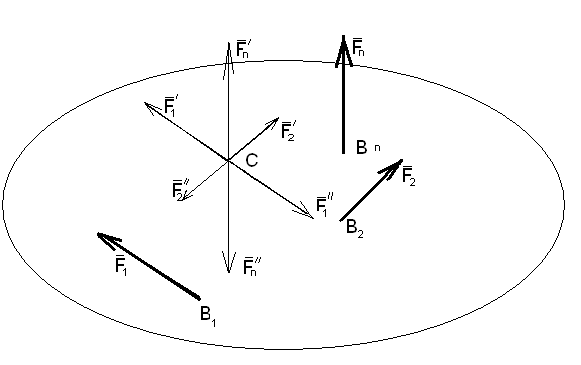
рис.1.4.2
В точку С параллельно перенесем все силы. Обозначим их
{ 1, 2,... n} . Чтобы действие сил на тело не изменилось, приложим пары сил { 1 1, 2 2, n n}
Cистему сходящихся сил заменим одной силой, которую назовем , главным вектором. Систему пар сил заменим одной парой с моментом (Мгл).
Мгл = М1+М2…Mn
Произвольно выбранная точка С, в которую мы переносим все силы, будет называться центром приведения системы.
Fгл равен геометрической сумме всех сил, а главный момент равен сумме всех приложенных моментов.
Таким образом, мы пришли к выводу, что система произвольных сил по своему действию эквивалентна главному вектору, приложенному в некотором центре приведения и главному моменту относительно этого центра приведения.
Главный вектор не зависит от положения центра приведения, а значение главного момента зависит от положения центра приведения.