1.2.3 Теорема о равновесии трех непараллельных сил.
Если три не параллельные силы, лежащие в одной плоскости, представляют собой уравновешенную систему сил, то их линии действия пересекаются в одной точке.
Рассмотрим тело, которое находится в равновесии под действием трех сил (рис.1. 2.4).
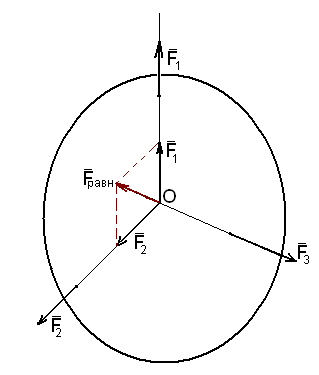
Рис.1.2.4
{
;
;
}~0
Доказательство:
Продолжим линии действия сил до пересечения в точке О, перенесем силы F1 и F2 в точку O. Заменим силы ; одной силой
{ + }= . В результате на тело будут действовать две силы
{ ; }~{ ; ; }.
Так как система находится в равновесии, то
{ ; }=0
По аксиоме 2, тело, находящееся под действием двух сил, будет в равновесии, если эти силы равны по модулю и противоположно направлены вдоль одной прямой, а если проходит через точку O, то и сила тоже должна проходить через эту точку.
Это условия необходимы, но не достаточны.
1.2.4 Аналитическое условие равновесия
Для равновесия свободного твердого тела, находящегося под действием системы сходящихся сил, необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на координатные оси была равна нулю.
Доказательство:
Необходимость
Система находится в равновесии { ; ... }~ ~0.
Fp2= Fpx2+Fpy2=0; Fpx=0; Fpy=0
Fpx=∑Fix → ∑Fix=0
Fpy=∑Fiy → ∑Fiy=0
∑Fx=0
→ Fp=0
∑Fy=0
Достаточность:
1.2.5 Основные понятия векторной алгебры
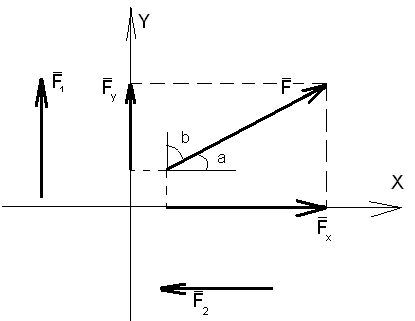
Рис. 1. 2.5
Если сила расположена под углом к оси, то проекция этой силы на ось X Fx=Fcosa , a проекция силы F на ось Y Fy=Fcosb .
Если сила расположена параллельно оси , то проекция на одну из осей равна нулю, а на другую ось самой силе. Проекция имеет знак «+», если направление проекции и направление оси совпадает .
Например на рис. 1.2.5
F1x=0
F1y=F1
F2x=-F2
F2y=0
1.2.6 Методика решения задач
1. Отбрасываем связи, заменяем реакциями.
2. Составляем расчетную схему.
3. Составляем уравнение равновесия.
4. Решаем систему уравнений равновесия.
5. Делаем проверку.
1.2.7 Пример решения задач
Определить реакции идеальных связей по данным рисунка 1.2.6.
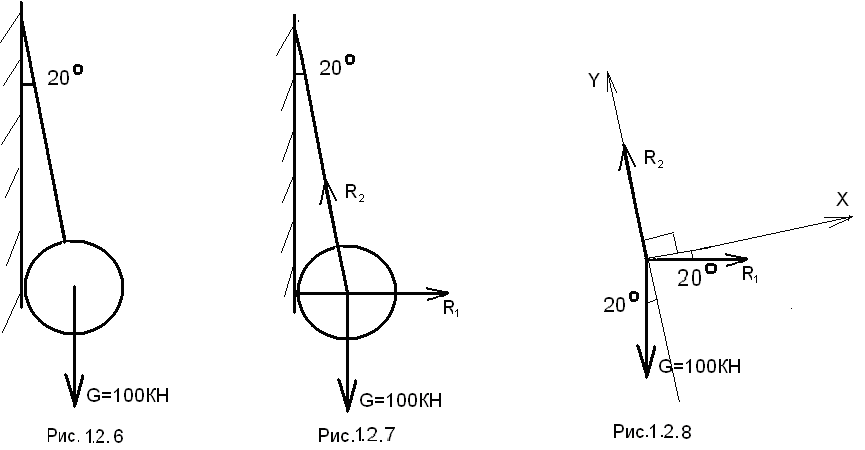
Решение:
1. Отбрасываем связи, заменяем реакциями (Рис.1.2.7).В данном примере две связи гибкая нить и гладкая опорная поверхность. В гибкой нити реакция направлена вдоль нити (R2). В гладкой опорной поверхности возникает одна реакция (R1), направленная перпендикулярно поверхности
2. Составляем расчетную схему (Рис. 1. 2.8). Для этого все силы переносим в одну точку, параллельно. Выбираем координатные оси (желательно, чтобы одна из осей совпадала с неизвестной силой).
3. Составляем уравнение равновесия.
ΣX= R1 cos20-G cos70=0
ΣY=-R1 cos70+R2 -G cos20=0
4. Решаем систему уравнений равновесия.
R1
×0,94
-100×0,342=0
R1=34,2/0,94=36,4КН
-35,4×0,342+R2-100×0,94 =0 R2=-12.4-94=-106,4 КН
5. Делаем проверку.
Для этого в расчетной схеме иначе выбираем оси и для новой расчетной схемы составляем уравнения равновесия и их решаем или решаем графически.
Проверка. Составим расчетную схему (Рис.1.2.9)
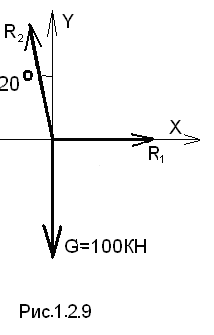
Составим уравнения равновесия
ΣX= R1-R2 cos70=0
ΣY=R2 cos 20 -G =0
Решим эту систему.
R2=100/0,94=106,4 КН
R1=R2×0,342=106,4 ×0.342=36,4КН
Решим данную задачу графически (Рис.1. 2.10).
Для этого выберем масштаб 1 КН= 10 см.
Откладываем в масштабе известную силу G в выбранном масштабе ( 100КН= 10 см) вертикально ( параллельно силе G в расчетной схеме).
Из начала силы G проведем линию параллельнуюR1 (под углом 90˚к силе G) , а из конца силы G проведем линию параллельную силе R2 ( под углом 20˚к силе G).
Пересечение данных линий даст значение сил R1 и R2
1.3 Пара сил
При изучении темы рассмотрим следующие вопросы:
1.3.1 Момент силы относительно точки.
1.3.2 Пара сил.
1.3.3 Теорема об эквивалентности пар.
1.3.4 Условия равновесия системы пар сил.
В результате изучения темы студент должен :
знать понятие пары сил, момента силы относительно точки, условие равновесия пары сил относительно точки.
После изучения темы необходимо ответить на следующие вопросы:
1.Что такое плечо силы относительно точки?
2. Когда момент силы относительно точки равен нулю?
3.Когда момент силы относительно точки положительный, а когда отрицательный?
4. Что называется парой сил?
5.Когда тело под действием системы пар сил находится в равновесии?
6. Чем характеризуется пара сил?