
- •5.03050901 “Бухгалтерський облік”
- •5.03050702 “Комерційна діяльність”
- •Пояснювальна записка
- •Тема 1. Елементи лінійної алгебри практична робота № 1 Тема. Розв’язування задач на виконання дій над матрицями. Обчислення визначників
- •Теоретичні відомості про визначники та їх властивості
- •Питання для самоперевірки знань, умінь
- •Виконаємо самостійно
- •Практична робота № 2 Тема. Розв’язування систем лінійних рівнянь основними методами: методом Гауса, за формулами Крамера
- •Питання для самоперевірки знань, умінь
- •Виконаємо самостійно
- •Практична робота № 3 Тема. Розв’язування систем лінійних рівнянь матричним методом
- •Теоретичні відомості про матричний спосіб розв’язування систем лінійних рівнянь
- •Питання для самоперевірки знань, умінь
- •Виконаємо самостійно
- •Тема 2. Аналітична геометрія практична робота № 4 Тема. Застосування рівнянь прямих до дослідження їх взаємного розташування, знаходження кута між ними
- •Теоретичні відомості про кути між прямими, взаємне розташування прямих в просторі
- •1. Кут між прямими, які лежать в одній площині і задані рівняннями:
- •2. Умова паралельності прямих.
- •Питання для самоперевірки знань, вмінь
- •Виконаємо самостійно
- •Практична робота № 5 Тема. Розв’язування задач на складання рівнянь ліній другого порядку: кола, еліпса, гіперболи, параболи
- •Питання для самоперевірки знань, умінь
- •Виконаємо самостійно
- •Тема 3. Вступ до математичного аналізу практична робота № 6 Тема. Границя функції. Обчислення границь функцій
- •Питання для самоперевірки знань, умінь
- •Виконаємо самостійно
- •Тема 5. Диференціальне числення функції однієї змінної
- •Питання для самоконтролю знань, умінь
- •Питання для самоконтролю знань, умінь
- •Виконаємо самостійно
- •Практична робота № 9 Тема. Схема дослідження і побудови графіка функції за допомогою похідної
- •Т еоретичні відомості. Загальна схема дослідження і побудови графіка функції. Алгоритм дослідження функції та побудови графіка
- •Питання для самоконтролю знань, умінь.
- •Виконаємо самостійно
- •Практична робота №10 Тема. Найбільше та найменше значення функції на відрізку. Розв’язування прикладних задач на застосування похідної. Задачі на максимум
- •Теоретичні відомості про найбільше і найменше значення функції на проміжку
- •Т еоретичні відомості про застосування похідної
- •Питання для самоконтролю знань, умінь
- •Виконаємо самостійно
- •Теоретичні відомості про правила диференціювання.
- •Частинні похідні.
- •Питання для самоконтролю знань, умінь.
- •Виконаємо самостійно
- •Практична робота №12 Тема. Знаходження екстремуму функції двох змінних. Застосування двох змінних в економічній теорії
- •Питання для самоконтролю знань, умінь.
- •Виконаємо самостійно
- •Тема 6. Інтегральне числення
- •Питання для самоконтролю знань, умінь
- •Виконаємо самостійно
- •Практична робота № 14 Тема. Розв’язування задач на обчислення визначених інтегралів частинами та заміною змінних
- •1. Визначений інтеграл та методи його обчислення
- •2. Метод підстановки у визначеному інтегралі.
- •3.Метод інтегрування частинами у визначеному інтегралі.
- •Питання для самоконтролю знань, умінь
- •Виконаємо самостійно
- •Практична робота № 15 Тема. Обчислення площ плоских фігур за допомогою визначеного інтеграла. Розв’язування прикладних задач
- •Теоретичні відомості про правила інтегрування та застосування визначеного інтегралу
- •1. Формула Ньютона – Лейбніца.
- •2. Застосування визначеного інтегралу до обчислення шляху за відомим законом зміни швидкості.
- •3. Обчислення площі плоскої фігури.
- •Питання для самоконтролю знань, умінь.
- •Виконаємо самостійно
- •Тема 7. Диференціальні рівняння практична робота № 16 Тема. Роз’язування лінійних диференціальних рівнянь з відокремлюваними змінними. Задача Коші
- •Теоретичні відомості про лінійні диференціальні рівняння з відокремлюваними змінними. Задача Коші
- •Питання для самоконтролю знань, умінь.
- •Виконаємо самостійно
- •Практична робота № 17 Тема. Розв’язування лінійних однорідних диференціальних рівнянь другого порядку зі сталими коефіцієнтами. Загальний та частинний розв’язки
- •Теоретичні відомості про диференціальні рівняння другого порядку зі сталими коефіцієнтами
- •Питання для самоконтролю знань, умінь
- •Література
- •Рецензія
Питання для самоперевірки знань, вмінь
Як визначити кут між прямими, що задані канонічними рівняннями ?
Сформулювати умову паралельності двох прямих, що задані канонічними рівняннями.
Сформулювати умову перпендикулярності двох прямих, що задані канонічними рівняннями.
Як залежить перпендикулярність та паралельність прямих від їх напрямних та головних векторів ?
Висновок__________________________________________________________________________________________________________________________________________________________________________________
Перевірив викладач ___________ Оцінка ___________ Дата ______________
Виконаємо самостійно
В-1 В-2
1. Знайти кут між прямими і :
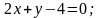
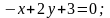
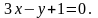
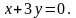
2. Скласти рівняння прямої, яка проходить через точку C і паралельна до прямої l:
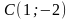
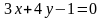
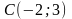
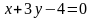
3. Скласти рівняння прямої, яка проходить через точку M і перпендикулярна до прямої l:
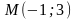
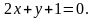
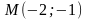
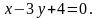
4. Скласти рівняння прямої, яка проходить через точку перетину прямих a і b і паралельна до c:
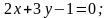
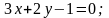
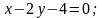
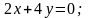
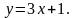
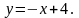
В-3 В-4
1. Знайти кут між прямими і :
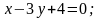
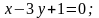
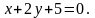
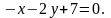
2. Скласти рівняння прямої, яка проходить через точку C і паралельна до прямої l:
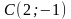
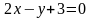
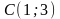
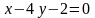
3. Скласти рівняння прямої, яка проходить через точку M і перпендикулярна до прямої l:
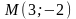
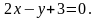
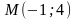
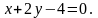
4. Скласти рівняння прямої, яка проходить через точку перетину прямих a і b і паралельна до c:
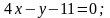
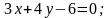
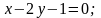
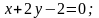
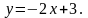
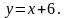
Практична робота № 5 Тема. Розв’язування задач на складання рівнянь ліній другого порядку: кола, еліпса, гіперболи, параболи
Мета роботи: навчитись складати рівняння кривих другого порядку за виглядом рівнянь ліній досліджувати їх особливості.
Наочне забезпечення та обладнання:
Інструкційні картки;
Приклади задач;
Роздаткові матеріали: опорні конспекти “Основні формули аналітичної геометрії”
Обчислювальні засоби.
Теоретичні відомості про коло.
Колом
називається множина точок площини,
рівновіддалених від даної точки, яка
називається центром кола. Рівняння кола
з центром у початку координат і радіусом
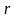 має
вигляд:
має
вигляд:
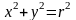 .
.
Рівняння
кола з центром в точці

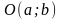 і радіусом
має вигляд:
і радіусом
має вигляд:
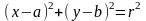
Рівняння кола в загальному вигляді записують так:
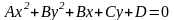 ,
,
де
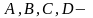 сталі
коефіцієнти.
сталі
коефіцієнти.
Завдання
1. Побудувати коло
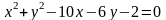 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача № 2. Складіть рівняння кола, яке проходить через точки
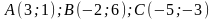 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теоретичні відомості про еліпс
Еліпсом
називається множина точок, сума відстаней
від яких до двох заданих точок, що
називаються фокусами, є величина стала
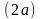 ,
більша за відстань між фокусами
,
більша за відстань між фокусами
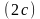 .
Рівняння еліпса, фокуси якого лежать
на осі
.
Рівняння еліпса, фокуси якого лежать
на осі
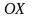 ,
має вигляд:
,
має вигляд:
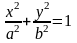 ,
,
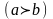 ,
,
де
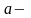 довжина
великої півосі,
довжина
великої півосі,
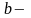 довжина
малої півосі.
довжина
малої півосі.
Залежність
між параметрами
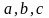 виражається співвідношенням:
виражається співвідношенням:
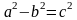 .
.
Ексцентриситетом еліпса називається відношення фокусної відстані до великої осі:
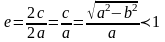
Якщо
фокуси еліпса лежать на осі
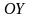 ,
то його рівняння має вигляд:
,
то його рівняння має вигляд:
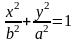 ,
.
,
.
В усіх задачах на еліпс передбачено, що осі симетрії еліпса збігаються з осями координат.
Задача
№3.
Скласти рівняння еліпса, якщо його
більша вісь дорівнює 10, а ексцентриситет
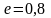 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача
№4.
Дано еліпс
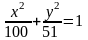 .
Обчислити його ексцентриситет.
.
Обчислити його ексцентриситет.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача
№ 5.Дано
еліпс
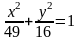 .
Знайти координати його вершин і довжини
осей.
.
Знайти координати його вершин і довжини
осей.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т еоретичні відомості про гіперболу
Гіперболою
називається геометричне місце точок
модуль різниці відстаней для кожної з
яких до двох даних фіксованих точок
(фокусів) є величина стала, менша за
відстань між фокусами і дорівнює
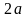 .
Найпростіше рівняння гіперболи:
.
Найпростіше рівняння гіперболи:
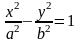 ,
,
де - дійсна піввісь гіперболи, - уявна піввісь.
Якщо
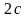 -
відстань між фокусами, то
-
відстань між фокусами, то
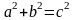 .
При
=
гіпербола називається рівносторонньою,
її рівняння має вигляд:
.
При
=
гіпербола називається рівносторонньою,
її рівняння має вигляд:
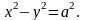 Фокуси гіперболи знаходяться на її
дійсній осі. Ексцентриситет гіперболи
– це відношення фокусної відстані до
довжини дійсної осі:
Фокуси гіперболи знаходяться на її
дійсній осі. Ексцентриситет гіперболи
– це відношення фокусної відстані до
довжини дійсної осі:
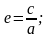
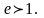
Асимптоти
гіперболи – прямі, що задаються рівняннями
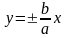 .
.
Якщо фокуси гіперболи лежать на осі , то її рівняння має вигляд:
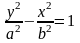 або
або
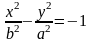 ,
,
а
рівняння асимптот такої гіперболи
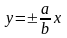 .
.
Рівняння
рівносторонньої гіперболи з фокусами
на осі
має вигляд:
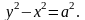
Гіперболи :
і
називаються спряженими.
В усіх задачах на гіперболу передбачено, що осі симетрії гіперболи співпадають з осями координат.
Задача
№1. Скласти
рівняння гіперболи, що має асимптотами
прямі
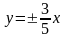 і проходить через точку (-5;2).
і проходить через точку (-5;2).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача
№2.
Скласти рівняння гіперболи, якщо її
вершини лежать в точках
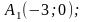
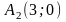 і фокуси в точках
і фокуси в точках
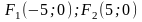 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача
№ 3.
Дано рівняння гіперболи
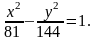 Знайти координати її вершин і фокусів.
Знайти координати її вершин і фокусів.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теоретичні відомості про параболу
Параболою
називається
геометричне місце точок, кожна з яких
однаково віддалена від заданої фіксованої
точки (фокуса) і від заданої фіксованої
прямої (директриси). Найпростіше рівняння
параболи має вигляд:
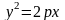 ,
де
,
де
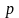 -
параметр, тобто відстань між директрисою
та фокусом. Рівняння директриси
-
параметр, тобто відстань між директрисою
та фокусом. Рівняння директриси
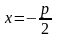 ,
фокус – це точка
,
фокус – це точка
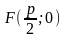 .
.
Є випадки задання параболи:
1)
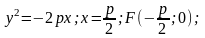
2)
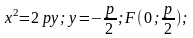
3)
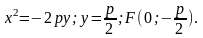
Рівняння парабол зі зміщеною вершиною мають вигляд:
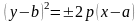 ;
;
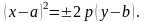
Задача № 4. Скласти рівняння параболи з вершиною в початку координат, знаючи координати фокуса (-2;0).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача
№ 5.
Визначити координати вершини і величину
параметра параболи, рівняння якої:
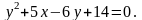 Знайти також координати її фокуса і
рівняння директриси параболи
Знайти також координати її фокуса і
рівняння директриси параболи
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
