4. Зависимость напряжения на конденсаторе от индуктивности контура

Рассмотрим последовательную цепь переменного тока, в которой оставим неизменными амплитуду напряжения генератора U_m = 1 В, емкость конденсатора С = 0,5 мкФ, частоту генератора  = 10³ рад/с, сопротивление R = 2 Ом.

В качестве расчетной формулы берем

.

Здесь ₀ и  задаются соотношениями (2).

Результаты расчета представлен на рис. 11. Таблица значений функции U_C,m (L) дана в приложении (Приложение, табл.1).

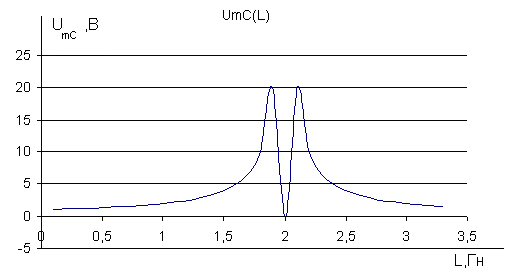
Рисунок 12 – Зависимость напряжения на конденсаторе U_mC (В) от индуктивности контура L (Гн)

Как видим, эта зависимость проявляет резонансный характер.

В работе следует детально проанализировать каждый график.

Выводы

В работе проведен анализ последовательной и параллельной электрической цепи переменного тока. Это простейшие виды линейных электрических цепей. В реальных схемах электрических соединений чаще встречаются смешанные соединения элементов. Однако и в рассматриваемых случаях обнаруживаются нетривиальные результаты, хотя мы не рассматривали переходные процессы и процессы, обусловленные воздействием на цепь сложного сигнала генератора.

Характерной особенностью последовательной электрической цепи при гармоническом воздействии (при гармоническом сигнале генератора) является то, что на каждом элементе цепи напряжение сложным, резонансным, образом зависит от частоты генератора в установившемся режиме колебаний, причем резонансные частоты на индуктивности, емкости и резисторе различны как и поведение напряжения на этих элементах на высоких и низких частотах. Все эти явления объединяются одним термином – резонанс напряжений.

Явления в параллельной электрической цепи отличаются коренным образом. На некоторой частоте полный ток в цепи становится минимальным. Эта группа явлений детально рассмотрена в работе. Она носит название резонанс токов.

В работе также рассмотрено напряжение на конденсаторе в зависимости от индуктивности контура. Эта функция также проявляет резонансное поведение.

Мы также рассмотрели энергетические соотношения в последовательной цепи без емкости. Показано, что максимальная выделяемая на резисторе энергия не зависит от величины его сопротивления и обратно пропорциональна частоте генератора.

Список использованных источников

1. Савельев И.В. Курс общей физики т.2: учебное пособие/ И.В. Савельев. - Москва: Наука, 1988. – 496 с.

2. Зисман Г.А. Курс общей физики т.2: учебное пособие/ Г.А. Зисман, О.М. Тодес. - Москва: Наука, 1965. – 366 с.

3. Сивухин Д.В. Курс общей физики т.2 Электричество: учебное пособие/ Д.В Сивухин. - Москва: Наука, 1974. – 519 с.

4. Ландау Л.Д. Механика./ Л.Д. Ландау, Е.М. Лившиц. - Москва: Наука, 1965. – 204 с.

5. Гречихин Л.И. Колебания и волны: учебное пособие/ Л.И. Гречихин, Н.И. Козарь, Н.И. Павлова. – Минск: МВИЗРУ ПВО, 1973. – 129 с.

Приложение 1

Таблица 1

Амплитуда напряжения на конденсаторе в зависимости от индуктивности контура

	Um, В		C, Ф		, рад/с			R, Ом		L, Гн			UmC(L), В
	1		5.10 - 7		103			2		0,1			1,0526
	1		5.10 - 7		103			2		0,2			1,1111
	1		5.10 - 7		103			2		0,3			1,1764
	1		5.10 - 7		103			2		0,4			1,25
	1		5.10 - 7		103			2		0,5			1,3333
	1		5.10 - 7		103			2		0,6			1,4285
	1		5.10 - 7		103			2		0,7			1,5384
	1		5.10 - 7		103			2		0,8			1,6666
	1		5.10 - 7		103			2		0,9			1,8181
	1		5.10 - 7		103			2		1			2
	1		5.10 - 7		103			2		1,1			2,2222
	1		5.10 - 7		103			2		1,2			2
	1		5.10 - 7		103			2		1,3			2,8571
	1		5.10 - 7		103			2		1,4			3,3333
	1		5.10 - 7		103			2		1,5			4
	1		5.10 - 7		103			2		1,6			5
	1		5.10 - 7		103			2		1,7			6,6666
	1		5.10 - 7		103			2		1,8			10
	1		5.10 - 7		103			2		1,9			20
	1		5.10 - 7		103			2		2			0
	1		5.10 - 7		103			2		2,1			20
	1		5.10 - 7		103			2		2,2			10
	1		5.10 - 7		103			2		2,3			6,6666
	1		5.10 - 7		103			2		2,4			5
	1		5.10 - 7		103			2		2,5			4
	1		5.10 - 7		103			2		2,6			3,3333
	1		5.10 - 7		103			2		2,7			2,8571
	1		5.10 - 7		103			2		2,8			2,5
	1		5.10 - 7		103			2		2,9			2,2222
	1		5.10 - 7		103			2		3			2
	1		5.10 - 7		103			2		3,1			1,8181
	1		5.10 - 7		103			2		3,2			1,6666
	1		5.10 - 7		103			2		3,3			1,5384

Примечание – Желательно столбцы таблицы полностью заполнять так, как это сделано в первом столбце. Не приводить слишком много знаков после запятой, а если это необходимо, то следует делать обоснование в тексте.

Приложение 2

Некоторые замечания по оформлению контрольной и курсовой работ

1. Использовать размер шрифта TNR 14. интервал полуторный, абзац – 5 позиций. выравнивание по ширине. В тексте исключить подчеркивания, выделения курсивом, жирным шрифтом, пропуски строк (увеличенный интервал между абзацами).

2. Ни в тексте, ни в заголовках ничего не подчеркивать и не выделять жиром.

3. Подписи под формулами делать в строчку, а не в столбик.

4. Расставлять знаки препинания после формул.

5. На самом рисунке указывать направление осей и наименование (не размерность!) отложенных физических величин.

6. Каждому графику должна соответствовать таблица, по которой он построен.

7. В работе следует:

Избегать эмоциональной окраски при изложении научных фактов (типа: «очень интересный вопрос…», «весьма актуальная проблема» и т.д.).

Избегать вопросов приоритета (типа: «В 1880 г. Россия закупила ректификационные колонны…»).

Исключить выражения типа: «легко (просто) показать (вывести, найти, заметить, получить, видеть, доказать…)», «как видно», «как следует», «очевидно», «тривиальные преобразования (выкладки)» и проч.

Не вести изложение от первого лица, типа: «Я показал, доказал, изучил, исследовал.» и проч. Следует писать: «Нами показано, получено, изучено…». Но еще лучше так: «В работе рассматривается, изучается, исследуется » и т.п.

Не начинать предложения с аббревиатур типа: т.о., т.е., т.к. и проч.

Не заканчивать раздел формулой, таблицей, подписью под рисунком.

Разделы начинать с новой страницы, подразделы – не обязательно.

Не разрывать по разным страницам подписи под рисунками или подписи таблиц. Если разрыв неизбежен – см. ГОСТ

Не отрывать заголовки подразделов от текста (не помещать на разные страницы).

Не писать: «приравниваем к 0», следует писать «приравняем к нулю»,

не писать: «равно 2», следует писать «равно двум». не писать: «  », следует писать «стремится к бесконечности». Не начинать предложение с номера формулы, так, недопустима запись в начале предложения вида «(8) – не единственное решение уравнения (5)». Следует начинать. например, так: «Выражение (8) – не единственное решение уравнения (5)».

При обозначении производных избегать использования точек над символами, следует избегать и штриховых обозначений. Лучше всего набирать в редакторе формул: , или соответственно.

Векторы не выделять жиром, в редакторе формул ставить вектор над символом: например, . Скалярное произведение обозначать круглыми скобками, разделяя перемножаемые векторы запятой, например ; аналогично, векторное произведение обозначаем квадратными скобками или . Если встречается выражение типа , то следует сопровождать его пояснениями: векторное произведение векторов (наименование, размерность) и вектора (наименование, размерность), вектор (наименование, размерность).

Индексы набирать увеличенным размером.

Общая теория решения дифференциальных уравнений в курсе общей физики не используется. Дифференциальное уравнение записывается на основе второго закона Ньютона или закона сохранения энергии. По таблице из методички записывается решение этого уравнения и методом подстановки следует убедиться, что это решение удовлетворяет заданному уравнению. Нелинейные дифференциальные уравнения, типа уравнения Ван дер Поля, могут быть выведены из физических соображений, проанализированы, но решать их и анализировать их нелинейные свойства не следует.

Подпись под рисунками набирать TNR 14, как и основной текст.

Если на графике на осях координат отложены деления с цифрами, то на таких осях стрелки не ставятся

Остальное - смотрите по стандарту.

8. По содержанию работы.

Во введении обязательно формулируются цели и задачи работы. Введение не должно занимать слишком большой объем. Лучше, если оно не содержит формул, таблиц, расчетов.

При выполнении работы всегда изучается какой-то колебательный процесс. В обзорной части (первый раздел, озаглавленный конкретно) следует указать порядки величин встречающихся при описании процесса. Они могут быть взяты из базового учебника, сборников задач или определены самостоятельно при выполнении лабораторной работы.

Для построения графиков процессов используем их аналитическое задание, т.е. функцию х(t). Продифференцировав ее, получаем функцию V (t) – скорость. Строим зависимость v(x) – фазовую траекторию. Для построения графиков данные удобно представлять в виде таблицы

t	x(t)	v(t)
0,1	0,5	1,7

Если требуется, таблицу расширяем, включая ускорения (это необходимо при построении соответствующих резонансных кривых).

Фазовая траектория задается зависимостью v(x).

При построении спектра колебаний следует руководствоваться разделом 2.1.19. по пособию «Физика колебательных процессов». Спектр затухающих колебаний строим по формулам 124, 125. Примерный вид этих спектров дан на рис. 37 -40 указанного пособия.

Предпочтительно масштаб графиков выбирать таким, чтобы они умещались на формате А4 и были информативными. Допускается разрывы осей (при различном поведении функций в различных областях).

При изучении затухающих колебаний определите коэффициенты сопротивления и затухания, добротность, логарифмический коэффициент затухания.

При выполнении экспериментальной работы в описании должны содержаться следующие разделы:

- описание установки;

- порядок проведения эксперимента;

- результаты работы (заполнить таблицу);

- обработка результатов (определение погрешностей и доверительного интервала);

- обобщение (обсуждение) результатов; выявление физических причин затухания (нарастания) колебаний осциллятора.

Результаты изучения колебательного процесса занести в таблицу, выбрав необходимые параметры или добавить при необходимости другие (указать их наименование, размерность).

Т	t1/2	t10		ω	ω0	ω0
m	L	J0	Jc	Lпривед	r	Q
δ	Δω/ω0	А0	А1/2	А10	δф	V

Здесь:

T – измеренный период затухающих колебаний, (наименование, размерность. ( Методичка. Глава 5б «Таблица наименований и размерностей физических величин»));

T₀ –период собственных (незатухающих) колебаний;

t_1/2 – время, за которое амплитуда колебаний уменьшилась в два раза;

t₁₀ – продолжительность десяти полных колебаний;

 - расчетный коэффициент затухания;

ω – циклическая частота колебаний (по измерениям);

ω₀ – собственная частота колебаний (расчетная);

m – масса осциллятора;

L – габариты осциллятора (описать подробно);

J₀ – момент инерции осциллятора относительно оси вращения ОО^՜

J_C - момент инерции осциллятора относительно оси проходящей через центр масс;

L_привед – приведенная длина осциллятора;

r – коэффициент сопротивления;

Q – добротность осциллятора;

δ – логарифмический декремент затухания;

Δω/ω₀ – относительная ширина полосы;

А₀ – начальная амплитуда (с указанием размерности);

А_1/2 – величина амплитуды в половину меньшая начальной;

А₁₀ - амплитуда после десяти периодов (или n периодов) колебаний;

δ_ф – дополнительный угол;

V – скорость осциллятора;

- ускорение осциллятора;

Ω – угловая скорость осциллятора (при вращательном движении).

Могут быть определены и другие физические величины, характеризующие колебательный процесс той или иной физической природы. Следует стремиться использовать эти и другие стандартные (прежде всего принятые в учебнике Савельева И.В.) обозначения

9. При оценке работы прежде всего обращается внимание на правильность оформления, затем учитывается полнота выполнения задания и самостоятельность его выполнения, и, наконец, учитываются оригинальность подхода к исследованию процессов.

10. При защите курсовой работы следует поощрять наличие презентации и плакатов при условии грамотного их оформления Доклад при защите должен содержать:

- цель работы;

- решаемые задачи;

- методы решения;

- полученные результаты;

- обобщения (применения);

- выводы

Продолжительность доклада – не более пяти минут.

5. Вычисления и построение графиков функций в табличном процессоре EXCEL