1.4. Закон стефана больцмана и вина

Для практического использования формул (1.16) – (1.18) необходимо знать, как зависит r^_ от длины волны  и температуры Т абсолютно черного тела. Характер экспериментальной зависимости (1.15) r^_ = f (, Т) для трех разных температур Т₃  Т₂  Т₁ приведен на рис. 1.4.

( )_max

Рис.1.4

Как показывает формула (1.13), площадь под кривой r^_ дает энергетическую светимость R^*_Т абсолютно черного тела при соответствующей температуре. Из рисунка 1.4 видно, что R^_Т увеличивается с ростом температуры, а максимум r^_ смещается в сторону более коротких волн (  _m3  _m2 _m1) .

На основе анализа экспериментальных данных было установлено, что

, (1.19)

, (1.20)

где =5,671· 10^-8 - постоянная Стефана-Больцмана,

b=2,91 · 10^-3 м · K - постоянная Вина.

Соотношение (1.19) – это закон Стефана-Больцмана, а соотношение (1.20) – закон смещение Вина (или первый закон Вина).

Закон смещения Вина объясняет, в частности, изменение цвета свечения нагреваемого тела от красного к голубоватому. При температурах, не превышающих комнатную, длина волн _m находится в инфракрасном диапазоне, при этом интенсивность излучения электромагнитных волн других диапазонов очень мала.

Максимальное значение спектральной плотности излучательности АЧТ связано с температурой следующей зависимостью (второй закон Вина):

, (1.21)

где C=1,29 · 10^-5 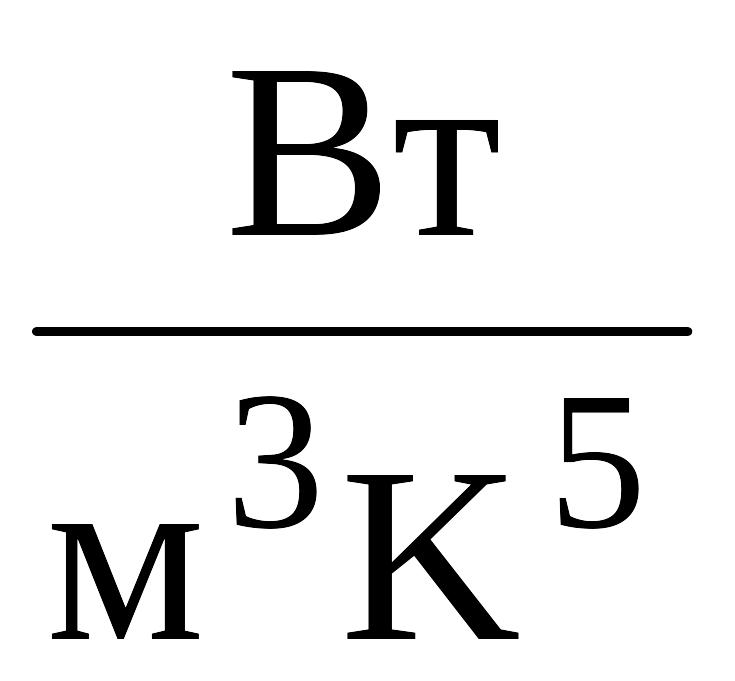- постоянный коэффициент.

Законы теплового излучения (1.19)-(1.21) весьма важны в практическом плане. Однако, это частные законы, которые не дают общей картины распределения энергии теплового равновесного излучения по длинам волн (частотам) при разных температурах.

1.5. Формула рэлея-джинса

Экспериментально установленный характер кривой не удавалось объяснить с позиций классической физики даже при самом тщательном рассмотрении.

Рэлей и Джинс предприняли попытку теоретически определить спектральную плотность излучательности =f(,T), исходя из классического закона о равнораспределении энергии по степеням свободы. Они рассматривали равновесное излучение как систему стоячих электромагнитных волн в замкнутой полости (рис.1.3) с идеально отражающими стенками. Каждой такой независимой волне приписывалась средняя энергия = kТ ( kТ - на энергию электрического поля волны плюс kТ – на магнитную энергию). Определив число независимых волн, Рэлей и Джинс получили следующий результат:

(1.22)

или

, (1.23)

где k – постоянная Больцмана,

с – скорость света в вакууме.

Формула Рэлея-Джинса в форме (1.22) или (1.23) удовлетворительно согласуется с экспериментом лишь в области малых частот (больших длин волн) и высоких температур – рис.1.5. При больших частотах наблюдается принципиальное отличие: согласно формуле Рэлея-Джинса при ( ), , тогда как в соответствии с опытом, при , .

Абсурдный результат получается, если, используя (1.23), вычислить энергетическую светимость АЧТ по формуле (1.13) при Т = const  0:

Это означает, что в неравновесных условиях такое тело должно было бы мгновенно остывать до температуры абсолютного нуля, причем в составе излучения обнаруживалась бы бездна ультрафиолетовых и рентгеновских лучей, что никак не соответствует реальности.



Рис. 1.5

Таким образом, факты свидетельствовали о том, что классическая физика неверно описывает тепловое излучение в области больших частот. Эта ситуация, известная в физике как “ультрафиолетовая катастрофа”, привела к необходимости пересмотра основ физики.