Транспортная задача.

К специальным типам задач линейного программирования относится и так называемая транспортная задача. Она возникает при планировании наиболее рациональных перевозок грузов (по критерию стоимости, по критерию времени). Методы линейного программирования позволяют решать такие задачи, но исходя из особенностей этих задач, были созданы специальные алгоритмы их решения.

Общая задача формулируется так:

Пусть в m пунктах отправления находятся соответственно ,…, единиц однородного груза, который должен быть доставлен n потребителям в количествах ,…, единиц. Заданы стоимости перевозок единиц груза из i-го пункта отправления в j-ый пункт назначения.

Пусть - количество единиц груза, перевозимого из i-го пункта отправления в j-ый пункт назначения. Тогда переменные должны удовлетворять условиям:

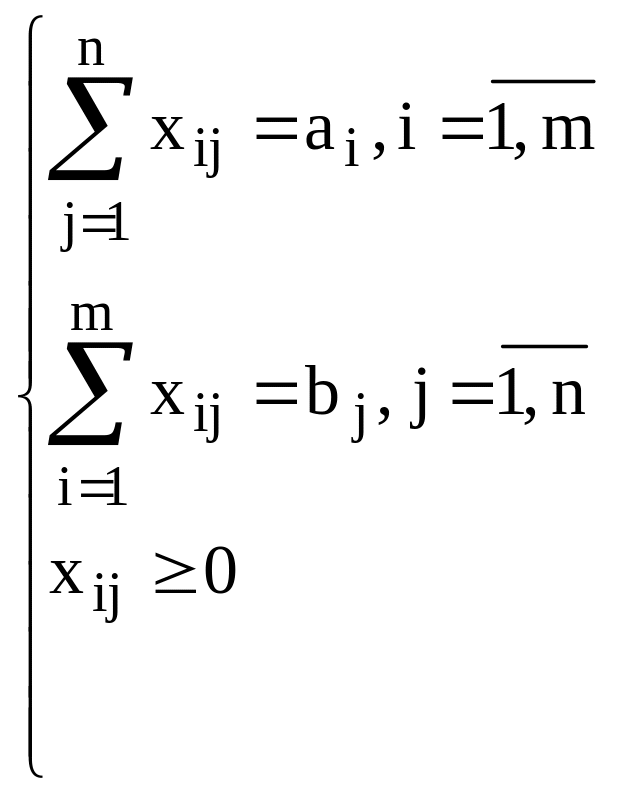
Суммарные затраты .

Замечание: Алгоритм решения транспортной задачи предполагает, что ее целевая функция стремится к минимуму, Однако если некоторая проблема требует максимизации целевой функции, перед тем, как применять для решения этой задачи стандартный алгоритм, его необходимо немного модифицировать. Например, мы намерены осуществить перевозку товаров таким образом, чтобы максимизировать общий доход. В этом случае нам необходима информация о единичных доходах от транспортировки товаров между всеми пунктами производства и назначения. Модификация заключается в умножении всех значений единичного дохода на (- 1), а затем задачу решают обычным образом.

Рассмотрим задачу:

Из 2-х пунктов A₁, A₂ к 3-м пунктам назначения В₁, В₂ , В₃ перевозится однородный груз с заданной матрицей стоимости перевозок.

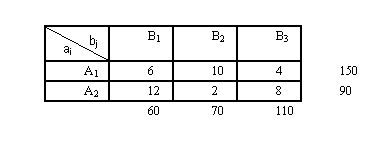
Применение этого алгоритма решения транспортной задачи требует соблюдения ряда предпосылок:

1. Должна быть известна стоимость перевозки единицы продукта из каждого пункта производства в каждый пункт назначения.

2. Запас продуктов в каждом пункте производства должен быть известен.

3. Потребности в продуктах в каждом пункте потребления должны быть известны.

4. Общее предложение должно быть равно общему спросу (в таком случае транспортная задача является сбалансированной). Если это условие не выполняется, т.е. задача не является сбалансированной, ее сводят к сбалансированной путем введения фиктивного поставщика (спрос >предложения) или фиктивного потребителя (спрос < предложения). При этом стоимость перевозок берется равной нулю.

В нашем случае задача сбалансирована, т.к. спрос = предложению (60+70+110=150+90).

Алгоритм решения транспортной задачи состоит из четырех этапов:

Этап1: Представление данных в форме стандартной таблицы и поиск любого допустимого распределения ресурсов.

Допустимым называется такое распределение ресурсов, которое позволяет удовлетворить весь спрос в пунктах назначения и вывезти весь запас продуктов из пунктов производства. Начальное распределение ресурсов может быть получено с помощью любого метода, позволяющего найти допустимое решение задачи. Один из таких методов — метод минимальной стоимости:

Алгоритм метода минимальной стоимости:

1. В клетку с минимальной единичной стоимостью записывают наибольшее возможное количество продукта.

2. Производится корректировка оставшихся объемов предложений и потребностей.

3. Выбирается следующая клетка с наименьшей стоимостью, в которую помещается наибольшее возможное количество продукта, и т. д. до тех пор, пока спрос и предложение не станут равными нулю.

4. Если наименьшее значение стоимости соответствует более чем одной клетке таблицы, выбор осуществляется случайным образом.