Гипербола, парабола

1. Составить каноническое уравнение гиперболы по следующим данным:

а) расстояние между вершинами равно 8, а расстояние между фокусами равно 10;

б) длина действительной оси равна 6, гипербола проходит через точку М (9; 4);

в) расстояние между фокусами 6, эксцентриситет равен 1,5;

г) уравнения асимптот , а расстояние между фокусами равно 20;

д) расстояние между директрисами равно , расстояние между фокусами равно 26;

е) эксцентриситет равен 1,5, расстояние между директрисами равно .

2. Составить каноническое уравнение гиперболы, если угол между асимптотами равен 60º, а гипербола проходит через точку М (4 ; 2).

3. Составить уравнение гиперболы, имеющей общие фокусы с эллипсом и проходящей через точку М (4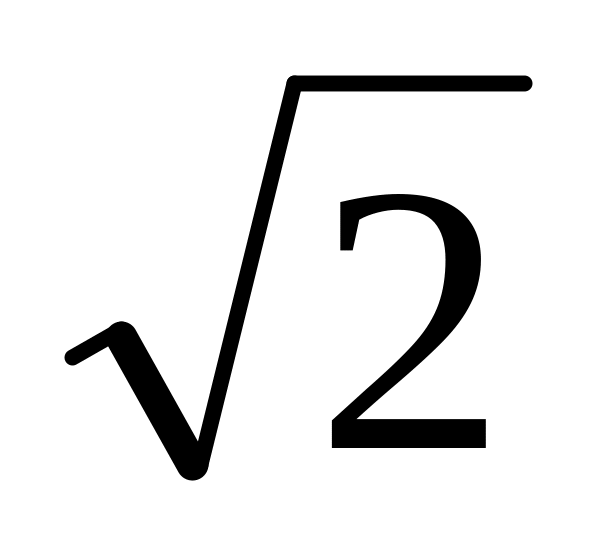 ; 3).

4. Дана гипербола . Написать уравнение сопряженной с ней гиперболы; найти эксцентриситеты и асимптоты данной и сопряженной гипербол.

5. По данному эксцентриситету в каждом из случаев определить угол между асимптотами гиперболы: а) ; б) .

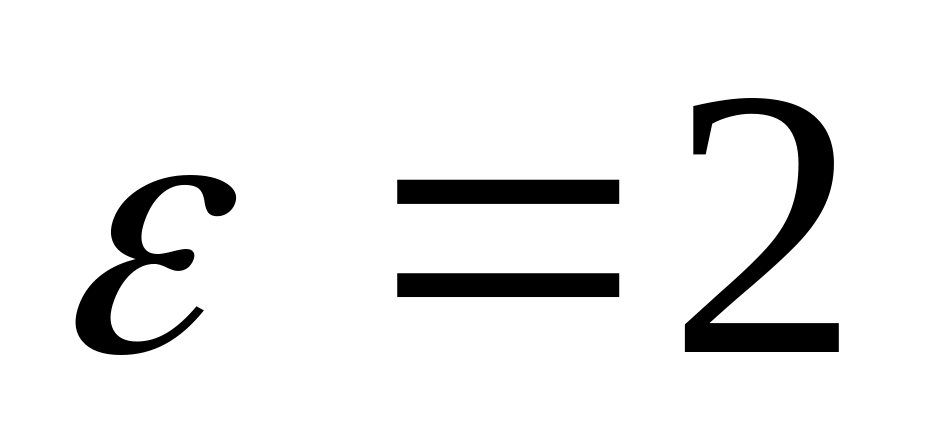6. Уравнения асимптот гиперболы 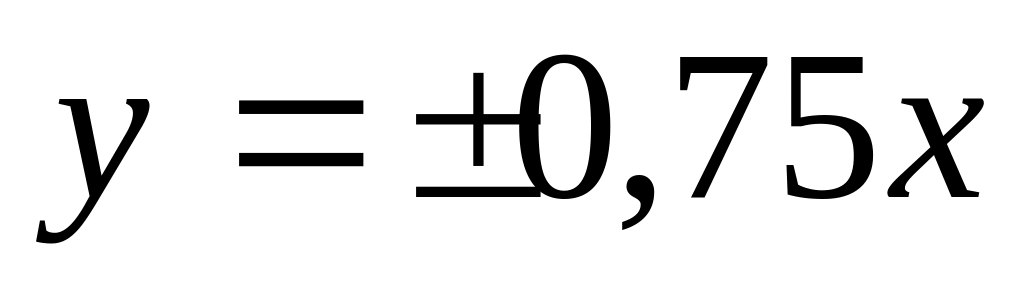. Найти эксцентриситет.

7. Составить уравнение гиперболы, эксцентриситет которой равен 3 и фокусы находятся в точках и .

8. Найти уравнение гиперболы, проходящей через точку М (-5; 3) и имеющей общие фокусы с равносторонней гиперболой .

9. Определить координаты фокуса F и составить уравнение директрисы для каждой из парабол:

а) ; в) ;

б) ; г) .

10. Составить каноническое уравнение параболы по следующим данным:

а) р = 3;

б) парабола проходит через точку Р (1; -4);

в) директриса определяется уравнением х + 3 = 0;

г) фокус имеет координаты (0; 5);

д) директриса имеет уравнение у + 12 = 0.

11. Вычислить фокальный радиус точки М параболы 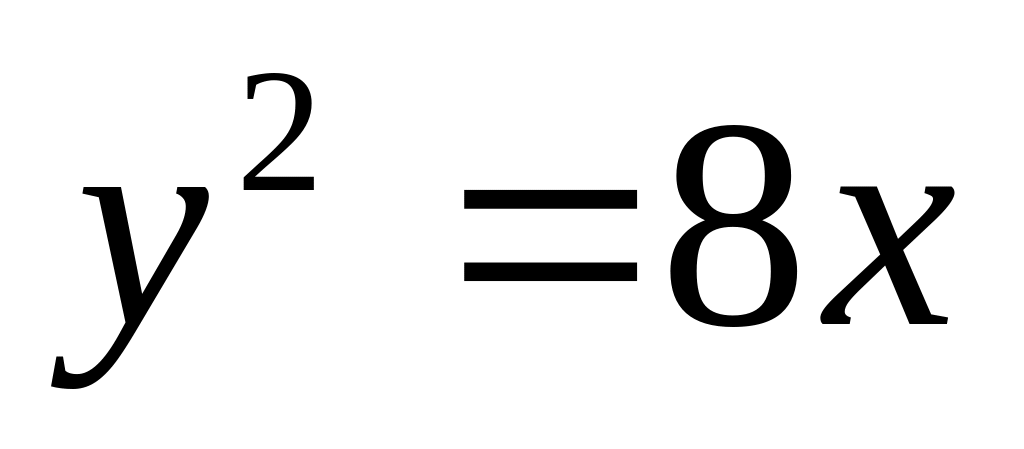, если ее абсцисса равна 8.

12. На параболе найти точку, фокальный радиус которой равен 9.

13. Составить уравнение параболы по следующим данным:

а) парабола симметрична относительно оси ОУ, фокус помещается в точке

F (0; 2), вершина совпадает с началом координат;

б) вершина находится в начале координат, парабола расположена в нижней полуплоскости, симметрична оси ОУ и р = 0,6;

в) фокус имеет координаты F(5; 0), а ось ординат служит директрисой;

г) парабола симметрична относительно оси ОУ и проходит через начало координат; прямая у = 2 пересекает параболу в точках с абсциссами 3 и -3.

14. Арка моста имеет форму параболы. Определить параметр параболы, зная, что пролет арок равен 24 м, а высота - 6 м.

15. Струя воды, выбрасываемая фонтаном, принимает форму параболы, параметр которой р = 0,1. Определить высоту струи, если известно, что она падает в бассейн на расстоянии 2 м от места выхода.

16. Эксцентриситет эллипса равен , а расстояние от точки М до директрисы равно 12. Вычислить расстояние от М до соответствующего фокуса.

17. Составить каноническое уравнение гиперболы, если уравнения директрис , расстояние от точки, взятой на гиперболе до фокуса, в два раза больше расстояния от этой точки до соответствующей директрисы.

18. Эксцентриситет гиперболы равен 2, фокальный радиус ее точки М равен 16. Найти расстояние от точки М до соответствующей этому фокусу директрисы.