Тема 5 Алгебраические линии и поверхности второго порядка

Теоретические вопросы

1. Дать определение окружности и записать ее уравнения. Как в каждом случае найти центр и радиус окружности?

2. Что называется степенью точки относительно окружности? Каков геометрический смысл степени точки?

3. Что называется радикальной осью двух окружностей? Радикальным центром?

4. Сформулировать геометрические и алгебраические определения эллипса, гиперболы, параболы. Записать канонические уравнения.

5. Основные элементы линий: фокальные радиусы, эксцентриситет, дирекориса, фокуса, асимптоты гиперболы.

6. Равносторонняя гипербола. Сопряженные гиперболы, параболы.

7. Директориальное свойство эллипса, гиперболы, параболы. Теорема Аполлония.

8. Построение эллипса, гиперболы, параболы.

9. Общее уравнение линии второго порядка.

10. Схема приведения общего уравнения линии второго порядка к каноническому виду.

11. Определение поверхности второго порядка. Уравнения.

12. Канонические уравнения поверхностей второго порядка. Классификация.

а) Центральные квадрики: эллипсоиды; гиперболоиды; конусы.

б) Нецентральные квадрики: параболоиды; цилиндры; квадрики, распавшиеся на две плоскости.

13. Линейчатые поверхности второго порядка и их прямолинейные образующие.

14. Поверхности вращения.

Задачи

Окружность. Эллипс

1. В прямоугольной декартовой системе координат даны уравнения:

а) ; б) ; в) ;

г) ;

д) .

Выяснить, какие из уравнений определяют окружность. Найти координаты центра и радиус каждой.

2. Определить расположение точки М (2; 7) относительно окружности .

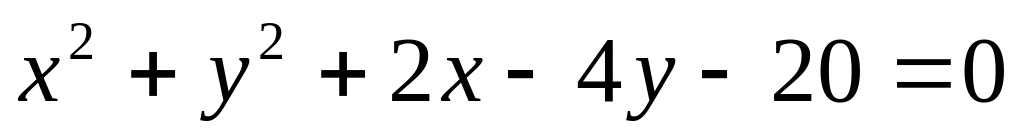3. Найти уравнение окружности, проходящей через три точки:

а) А (4; 6), В (-2; -2), С (-2; 6); б) А (1; -4), В (4; 5), С (3; -2).

4. Составить уравнение окружности с центром в точке С (5; 2), касающейся прямой .

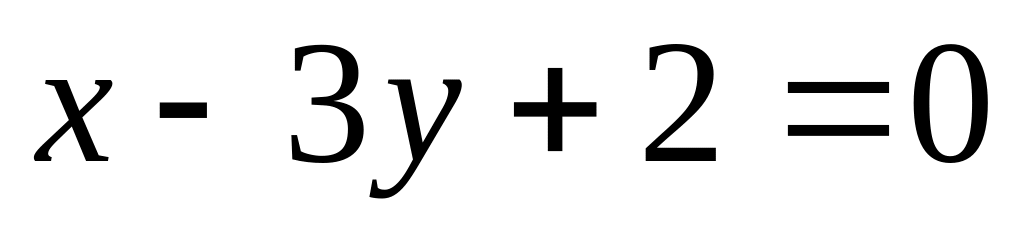5. Найти уравнение множества точек, для каждой из которых сумма квадратов расстояний от двух точек А (-1; 2) и В (1; 4) есть величина постоянная, равная 22.

6. Найти множество точек плоскости, имеющих одну и ту же степень относительно данной окружности.

7. Доказать, что радикальная ось двух окружностей есть прямая, перпендикулярная к линии центов.

8. Найти длины полуосей и координаты фокусов:

а) ; б) .

9. Найти точки, принадлежащие эллипсу 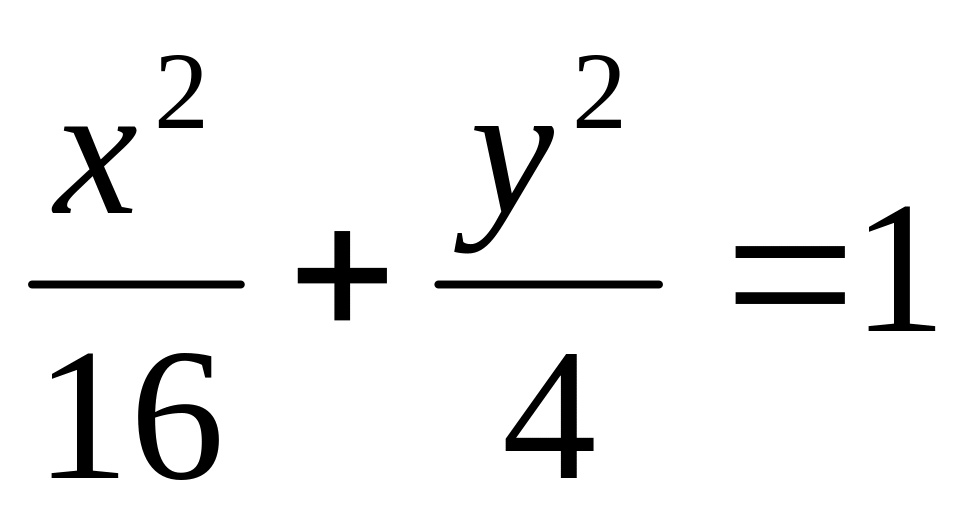абсциссы которых равны:

а) 2; б) 3; в) 1.

10. Длина большой полуоси эллипса равна 6, эксцентриситет - 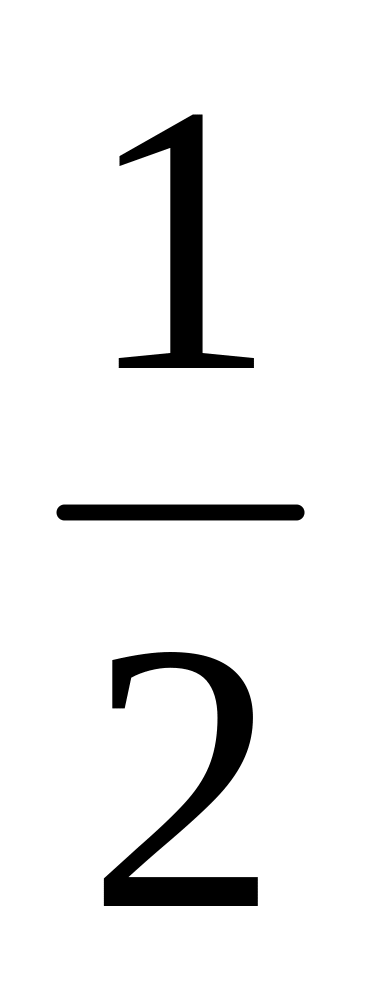, а расстояние точки М эллипса до фокуса 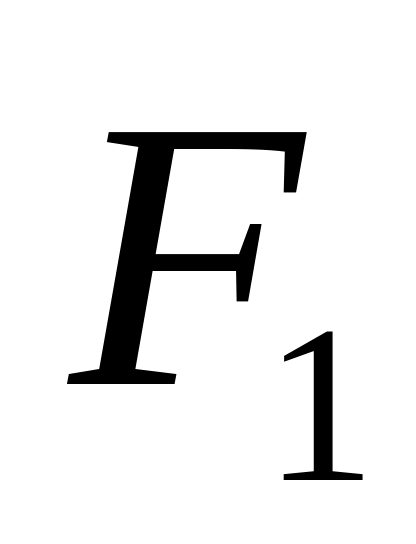равно 7. Найти расстояние 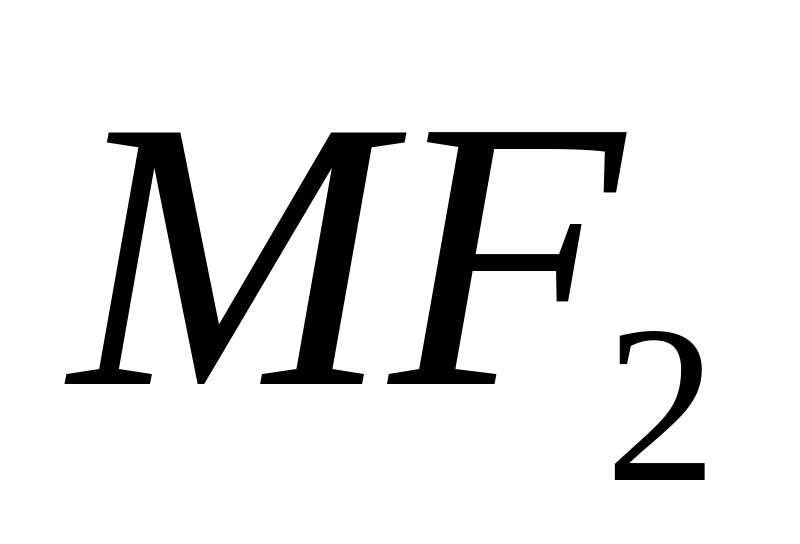и координаты точки М.

11. Составить каноническое уравнение эллипса, если:

а) координаты вершин эллипса - , , , ;

б) фокальное расстояние равно 10; малая полуось – 5;

в) расстояние между фокусами равно 8, а эксцентриситет - ;

г) эллипс проходит через точку М (-3; ) и расстояние между фокусами равно 6.

12. Написать уравнение директрис эллипса 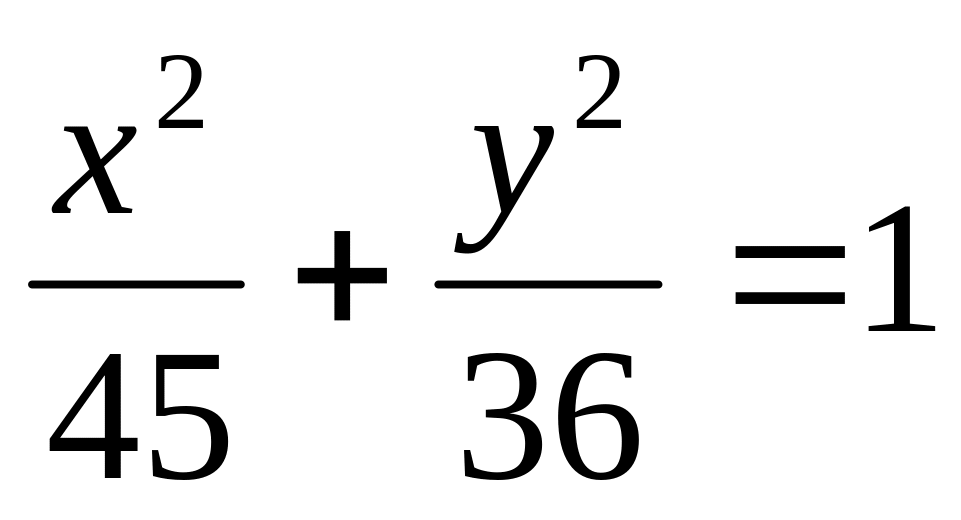и найти расстояние между ними.

13. Составить уравнение эллипса, зная, что:

а) расстояние между директрисами равно 12, а большая ось равна ;

б) директрисы заданы уравнениями х = 12 и х = - 12, а а эксцентриситет равен .

14. Найти эксцентриситет эллипса, зная, что расстояние между его директрисами в 4 раза больше расстояния между фокусами.

15. На эллипсе, определяемом уравнением 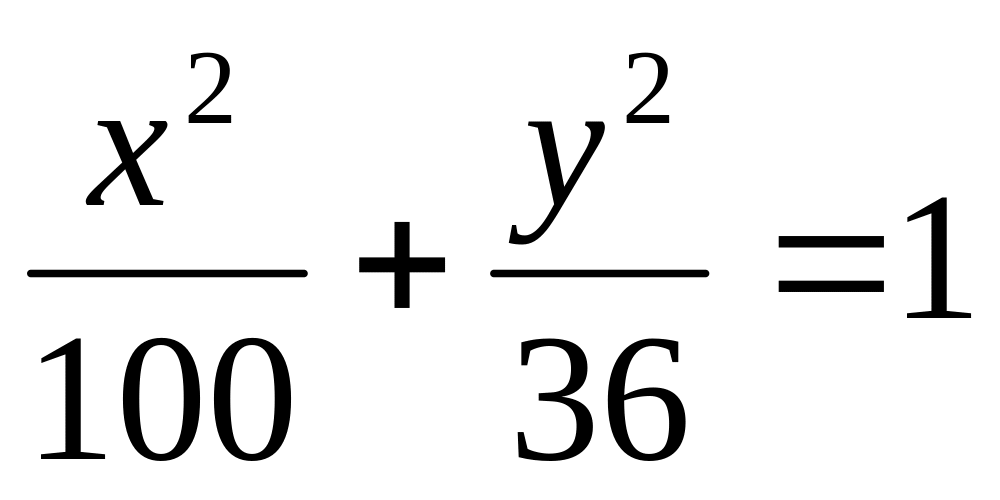, найти точки, расстояние от которых до правого фокуса в 4 раза больше расстояния до левого фокуса.

16. Эллипс проходит через две противоположные вершины квадрата ABCD, и его фокусами являются две другие вершины этого квадрата. Написать каноническое уравнение эллипса и уравнение его директрис, если АС = 2 М.

17. Найти длины полуосей и координаты фокусов гипербол:

а) ;

б) .