Глава 1. Электрические цепи Контур цепи — это замкнутый путь из ветвей. Например, в цепи

Эквивалентны

а^

N

4

г"

б

уч

( ^

N

Ветвь А

3 ветви

1 вел

Рис. 3

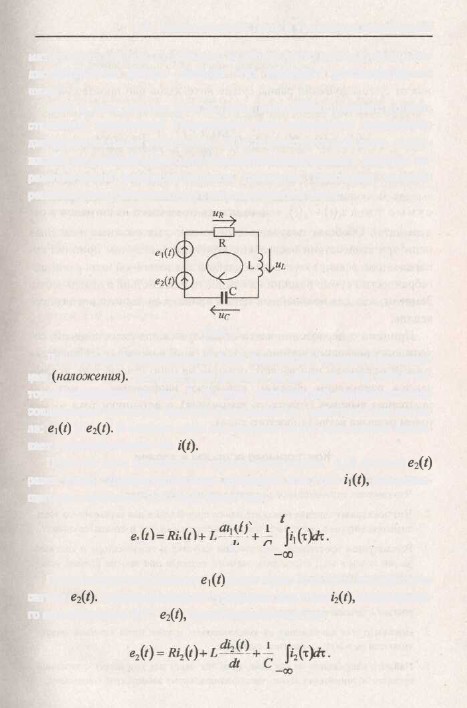
Для расчета цепей недостаточно знать рассмотренные выше три

уравнения элементов. В сложной цепи в общем случае токи и напря-

жения на элементах оказываются связанными друг с другом. Для опи-

Рис. 4

сания взаимосвязи токов и напряжений на р а з н ы х ветвях использу-

ются уравнения соединений (законы Кирхгофа).

Первое уравнение соединений (первый закон Кирхгофа) устанав-

ливает взаимосвязь токов в узле (рис. 5). В узле заряды не могут нака-

Рис. 5

пливаться или исчезать. Для узла выполняется закон сохранения заря-

да — сколько зарядов переносится к узлу втекающими токами,

столько же зарядов выходит из узла. После дифференцирования по

времени уравнений, описывающих заряды, получаем первый закон

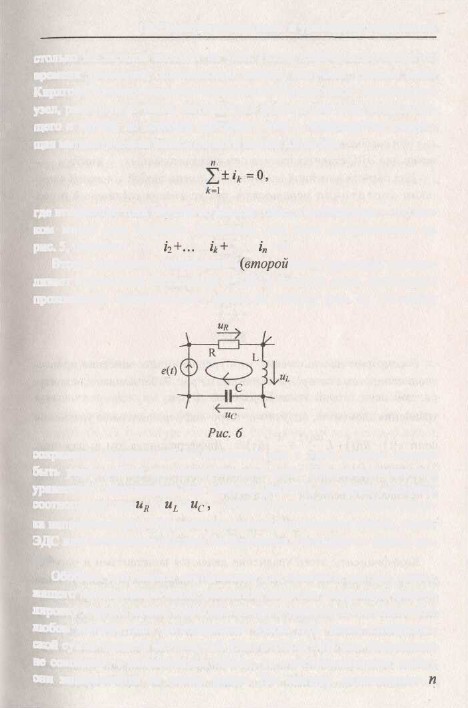
Кирхгофа (первое уравнение соединений): сумма токов, втекающих в

узел, равна сумме токов, вытекающих из узла. Для узла, объединяю-

щего п ветвей, по которым протекают токи 4, используется следую-

щая математическая запись первого закона Кирхгофа

где втекающие токи берутся со знаком плюс, а вытекающие — со зна-

ком минус или наоборот. Например, для узла, изображенного на

рис. 5, получим: + i\ - /2+... - 4+ ... + /„ = 0.

Второе уравнение соединений {второй закон Кирхгофа) устанав-

ливает взаимосвязь напряжений и ЭДС в контурах цепи. Рассмотрим

прохождение положительного заряда по контуру (рис. 6). По закону

сохранения энергии работа сторонних сил в этом контуре должна

быть равна работе сил электрического поля. Продифференцировав

уравнение, связывающее эти энергии (работы), по заряду, получим

соотношение: е = ик + UL + ис, — второй закон Кирхгофа. Если стрел-

ка напряжения или ЭДС противоположна направлению обхода, то эти

ЭДС или напряжение должны записываться в формулу со знаком ми-

нус.

Обобщая полученное соотношение для сложного контура, содер-

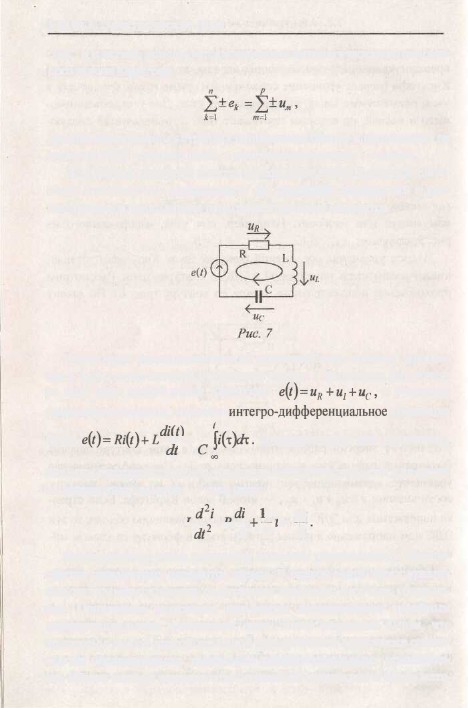
ЭДС и р ветвей, используется следующая математическая запись вто-

рого закона Кирхгофа

-t

UR

±и-

где при согласованных стрелках направления обхода и напряжения на

ветви или ЭДС ставится плюс, а при несогласованных — минус.

Для расчета линейной электрической цепи любой конечной слож-

ности д о с т а т о ч н о использовать два уравнения соединений и рас-

смотренные в предыдущем параграфе уравнения элементов.

Рассмотрим использование этих уравнений для описания процес-

уравнения элементов, получим интегро-дифференциальное уравнение

цепи e(t)=Ri(t)+L

di(C\

dt

+

с

1 'г

и(т)Л. Дифференцируя это выражение,

«,

получим дифференциальное уравнение электрической цепи для одной

из неизвестных величин — тока цепи:

d i „di I . de

T

2

Коэффициенты этого уравнения являются константами и опреде-