Для
цепи, содержащей как источники напряжения,
так и источни-3.4. Свойства линейных цепей
ки тока, принцип суперпозиции формулируется следующем образом:
реакция на множество источников в цепи равна сумме реакций на ка-
ждый из источников в отдельности. Под реакцией здесь понимаются
или ток, или напряжение на любом элементе цепи.
На практике метод наложения удобно использовать при расчете
напряжения или тока в некоторой одной ветви сложной цепи. В нача-
ле учитывается первый источник и рассчитываются частичные напря-
жение или ток ветви, вызванные одним этим источником. Эта проце-
дура повторяется последовательно для остальных источников.
Результирующие напряжения и токи находим как суммы частичных
напряжений или токов. Наиболее часто метод наложения использует-
ся при расчете напряжения или тока через нагрузку.
Кроме принципа суперпозиции при расчетах сложных цепей часто
используют теоремы об эквивалентных источниках. Различают тео-
рему об эквивалентном источнике напряжения и теорему об эквива-
лентном источнике тока.
а)
б)
Рис. 1
Теорема об эквивалентном источнике напряжения (рис. 1) форму-
лируется следующим образом. Любую по сложности электрическую
цепь, имеющую два зажима для подключения нагрузки, можно заме-
нить эквивалентным источником напряжения. ЭДС этого источника
равна напряжению холостого хода на зажимах цепи, а внутреннее со-
противление равно сопротивлению между зажимами цепи при исклю-
чении из цепи источников (методами короткого замыкания для ЭДС и
холостого хода для источников тока).
Пример такого преобразования показан на рис. 1: на рис. 1, а пока-
зана сложная электрическая цепь, а на рис. 1,6 — эквивалентный ис-
точник напряжения. Докажем теорему, используя рис. 2. На этом ри-
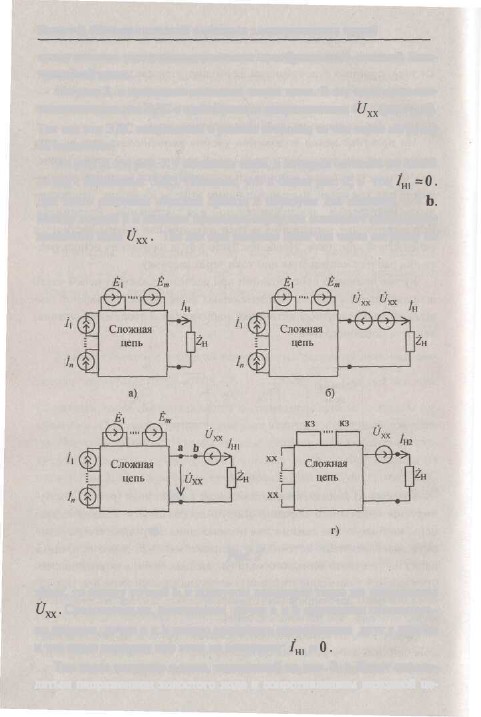
сунке
показан ряд последовательных
преобразований сложной элек-
трической
цепи.
На
рис. 2, а приведена исходная схема цепи.
В эту цепь дополни-
тельно
вводим две ЭДС с одинаковыми напряжениями
t/xx
(рис.
2, б).
Так
как эти ЭДС направлены в разные стороны,
то ток через нагрузку
не
изменится.
На
рис. 2, в и рис. 2, г показаны цепи, в которых
осталось по однойГлава 3. Методы анализа сложных электрических цепей
из двух введенных ЭДС. Покажем, что в схеме рис. 2, в ток /н, =0.
Для этого разорвем верхний провод и образуем два контакта а и Ь.
Между точкой а и нижним проводом-корпусом возникает напряжение
холостого хода U^. Так как при разрыве цепи ток через нагрузку не
в)
Рис. 2
течет, то между точкой b и корпусом возникает такое же напряжение
f/xx. Следовательно, потенциалы точек а и b одинаковы относитель-
но корпуса, точки а и b можно соединить проводником друг с другом
и ток через нагрузку при этом не возникает: /Н1 = 0.
Ток через нагрузку в цепи, показанной на рис. 2, г, будет опреде-
ляться напряжением холостого хода и сопротивлением исходной це-
пи,
в которой исключены все источники. В
соответствии с принципом
суперпозиции
/н
=
/Н|
+
/ ш
.
Так как первое слагаемое в правой части
приведенного
равенства равно нулю, то теорема
доказана.
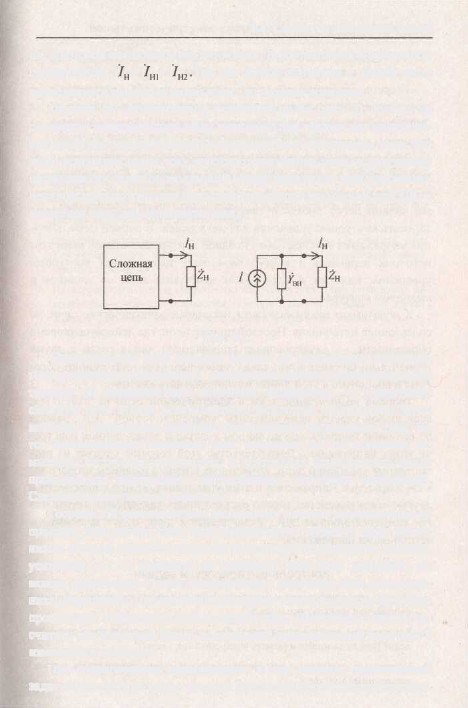
Теорема
об эквивалентном источнике тока (рис.
3): любую по
сложности
электрическую цепь, имеющую два зажима
для подключе-
ния
нагрузки, можно заменить эквивалентным
источником тока. Ток
этого
источника равен току короткого замыкания
цепи, а внутренняя
проводимость
равна проводимости между зажимами цепи
при исклю-
чении
из цепи источников (методами короткого
замыкания для ЭДС и
холостого
хода для источников тока).
Рис.
3
Доказательство
этой теоремы следует из взаимосвязи
источника3.4. Свойства линейных цепей
тока и источника напряжения. Используем вначале доказанную выше
теорему об эквивалентном источнике напряжения — представим
сложную цепь в виде эквивалентного источника напряжения. Затем
источник напряжения заменим эквивалентным источником тока. Но
ток эквивалентного источника тока находится как ток короткого за-
мыкания источника напряжения, а внутренняя проводимость равна
проводимости внутреннего сопротивления источника напряжения.
Следовательно, теорема доказана.
Теоремы об эквивалентных источниках широко используются на
практике при расчете тока через изменяемую нагрузку, когда источ-
ником сигнала являются сложные устройства: передатчики, модемы,
усилители и т. п. Несмотря на сложность всех этих устройств, их
можно представить в виде эквивалентных источника тока или источ-
ника напряжения. При изменении нагрузки в этом случае не требуется
производить перерасчет всей сложной цепи. Достаточно заново рас-
считать ток в простой схеме, содержащей эквивалентный источник и
измененную нагрузку.
При теоретических исследованиях и при решении практических
задач используются также теорема (принцип) обратимости (взаимно-
