Глава 10. Цифровая обработка сигналов

помощью дискретного преобразования Фурье (ДПФ). ДПФ определя-

ет представление дискретного или цифрового сигнала на конечном

интервале времени в виде суммы дискретных гармонических сигна-

лов.

Известно, что аналоговый периодический сигнал s(t), принадле-

жащий на отрезке времени Т пространству L\, можно представить в

виде ряда Фурье

где e— базисные гармонические функции. Q = 2п/Т — частота

основной гармоники, Т— период.

Продискретизируем указанные базисные функции и рассмотрим

jnni

= e "'

. 2it ,

•^~77~*

д

=e »

J-^nt

,2u ,

,

(1)

где n — номер гармоники, k — номер отсчета, N= 77?д — объем вы-

борки, т. е. число анализируемых отсчетов сигнала на отрезке време-

ни, равном Т. В большинстве современных устройств ЦОС использу-

ются объемы выборки N>512.Номер гармоники и можно

рассматривать как нормированную частоту, а номер отсчета k — как

нормированное время. Все значения базисных функций (1) располо-

жены на окружности единичного радиуса.

Аи = 2

При N = 8 эти значения показаны на рис. 1 в момент времени, со-

ответствующий k=l. Из анализа рис. 1 следует, что только восемь

первых гармоник отличаются друг от друга своими значениями. Зна-

чения восьмой гармоники совпадают со значениями нулевой гармони-

ки; девятой — с первой и т. д. Аналогичный вывод получим для дру-

гих моментов времени при k = 2, 3, 4, ... . Следовательно, для

представления цифрового сигнала базисная система должна включать

только N базисных функций. Число независимых гармоник, образую-

щих полную систему, равно объему выборки. Действительно, дис-

кретные сигналы, заданные N отсчетами, образуют евклидово про-

странство конечной размерности, равной N. Поэтому любой базис в

этом пространстве содержит N базисных функций.

Таким образом, для представления N отсчетов дискретных сигна-

*(*) = £С„«" .

и=0

^-1

/llnt

(2)

Здесь С„ — комплексная амплитуда и-й гармоники в спектре дис-

кретного сигнала.

Для определения коэффициентов С„ умножим левую и правую

части формулы (2) на базисную функцию ехр(-/2лрА:/ N) и просум-

мируем получившиеся произведения по k:

Щ

2Х*)е'"' =

*=0

*=0 V

-J^ft

Учитывая ортогональность дискретных базисных функций

N ПРИ

"

=

получим формулу для расчета спектральных коэффициентов в разло-

жении (2)

Формула (3) носит название прямого дискретного преобразования

Фурье (ДПФ), а формула (2) — обратного дискретного преобразова-

ния Фурье (ОДПФ). Отметим, что ДПФ и ОДПФ вводятся для перио-

дических последовательностей. Однако эти преобразования можно

применять для представления последовательностей конечной длины,

если последние периодически продолжить.

Дискретное преобразование Фурье широко используется для рас-

чета спектров сигналов. Кроме того, прямое и обратное преобразова-

ния Фурье применяют для построения цифровых фильтров в соответ-

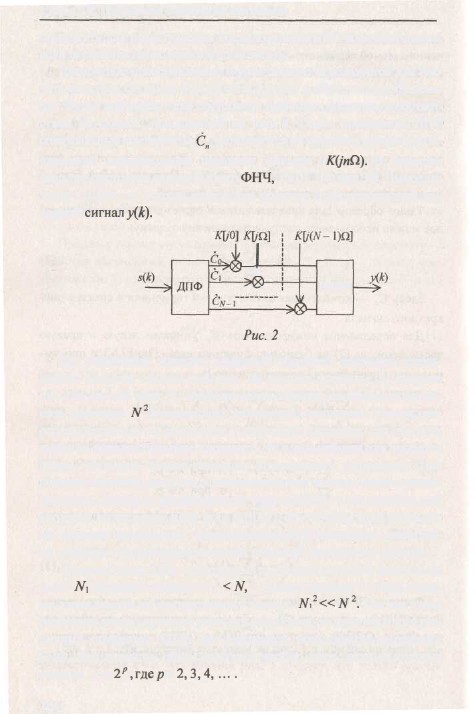
ствии со схемой, приведенной на рис. 2. После проведения ДПФ

спектральные компоненты С„ умножаются на заданные значения ком-

плексного коэффициента передачи фильтра K(jnQ). В качестве

фильтра-прототипа можно выбрать ФНЧ, ФВЧ, ПФ или ЗФ. Выполняя

затем ОДПФ, на выходе устройства получим отфильтрованный вы-

ходной сигнал y(k).

1

~jA7)

1у

ОДПФ

N/SS

Рис.2

Для увеличения точности цифровой обработки сигналов исполь-

236