Экспоненциальный рост опухолей

Характерной чертой роста опухоли является прогрессивное уве­личение числа клеток. Каждая вновь возникающая клетка получа­ется путем деления материнской клетки на две дочерних. Поэтому приближенно дифференциальное уравнение роста числа опухолевых клеток может быть записано в виде:

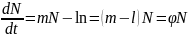(1)

В этом уравнении производная 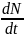есть скорость, с которой увеличивается число клеток опухоли, член mN представляет собой скорость размножения опухолевых клеток, пропорциональную (с ко­эффициентом пропорциональности m) общему числу клеток. Про­изведение lN характеризует собой скорость убыли опухолевых клеток, обусловленную различными причинами (гибель клеток, вымы­вание из опухоли током крови и т. п.) Разность факторов размножения m и убыли l опухолевых клеток равна 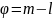. В ре­альных случаях можно полагать, что m>l. Т.е. опухолевые клетки возникают с большей скоростью, нежели происходит их гибель. Таким образом, для растущей опухоли величина 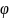>0. В действи­тельности картина опухолевого роста значительно сложнее. Ско­рость роста опухолей зависит от локализации, от условий кровоснабжения, изменений степени зло­качественности опухолевых клеток и т. п. Влияние всех этих фак­торов можно пытаться учесть в дифференциальном уравнении (1). Во многих случаях это не изменяет общего описания развития процесса, хотя и усложняет математические выкладки.

Интегрирование уравнения (1) приводит к экспоненциальной зависимости числа опухолевых клеток от времени:

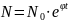(2)

где 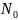− исходное число клеток растущей популяции. Нетрудно перейти от этой формулы к выражению для увеличения со време­нем объема опухоли. Предположив, что объем опухоли V равен произведению числа опухолевых клеток на объем клетки 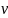, т. е. 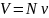получим

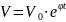(3)

Таким образом, кинетический закон роста опухолей выражается достаточно простой математической функцией (экспоненциальный закон роста). Темп роста опухоли определяется значением вели­чины в показателе экспоненты.

Линейный рост опухолей

Наибольшее приближение к экспоненте наблюдается обычно в ранний период развития опухоли. По мере того, как масса опухоли увеличивается, ее внутренние и наружные участки оказываются в неодинаковых физиологических условиях, что отражается на скоро­сти размножения клеток.

Математическое рассмотрение вопроса показывает, что при неко­торых допущениях относительно доли делящихся клеток следует ожидать линейной зависимости размеров опухоли от времени. Для вычисления растущего объема опухоли 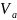, представляющего собой сферический слой толщины h, необходимо из объема шара радиуса (r+h) вычесть объем шара радиуса r. При этом для величины («активный объем») находим:

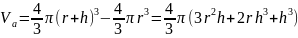(4)

Увеличение общего объема опухоли в данном случае происходит лишь за счет размножения клеток «активного объема» . Поэтому, считая, по-прежнему, что клетки «активной» части объема делятся со скоростью, пропорциональной наличному их количеству, можно записать:

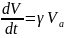(5)

где V − общий объем опухоли, 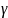− величина, характеризующая темп роста. Отсюда 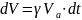. Здесь dV − увеличение всего объема за период времени dt. Подставляя вместо его выраже­ние из формулы (4), получим:

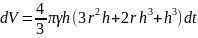(6)

Представим увеличение объема шара радиуса r через увеличение его радиуса dr. Аналогично предыдущему, увеличение объема шаpa можно представить как разность объемов двух радиусов r+dr и r:

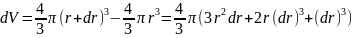
Поскольку за малое время dt радиус опухоли меняется на малую величину dr, в выражении для dV величины 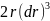и 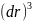будут много меньше 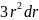, поэтому ими можно пренебречь. Следовательно:

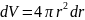(7)

Подставляя это выражение в формулу (5) и деля обе части на 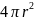получим:

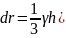(8)

Если толщина растущего слоя h мала по сравнению с радиусом опухоли r, т. е. величина h/r много меньше единицы, то величинам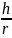и и в формуле для dr можно пренебречь.

Окончательно получаем:

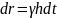
Этому дифференциальному соотношению удовлетворяет единст­венная функция r, зависящая следующим образом от t:

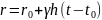(9)

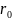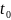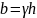где — радиус опухоли в момент времени . Иными словами, получаем линейную зависимость роста радиуса (или диаметра) опу­холи со временем. Величина определяет угол наклона пря­мой, являющейся графиком этой функции, к оси времени t, т. е. ха­рактеризует скорость роста опухоли.