Коэффициент восстановления при ударе

Для решения задач по теории удара основного уравнения (2) или вытекающих из него уравнений (3) и (4) оказывается недостаточным. Объясняется это тем, что величина ударного импульса, возникающего при соударении двух тел, зависит не только от масс и скоростей этих тел до удара, но и от упругих свойств. Для характеристики этих свойств в теорию удара вводится величина, называемая коэффициентом восстановления.

Рассмотрим шар, падающий вертикально и притом поступательно на неподвижную горизонтальную плиту. Для удара, который при этом произойдет, можно различить две стадии. В течение первой стадии скорости частиц шара, равные в момент начала удара V убывают до нуля. Шар при этом деформируется (плиту считаем абсолютно жесткой), и вся его начальная кинетическая энергия переходит во внутреннюю потенциальную энергию деформированного тела. Во второй стадии удара шар под действием внутренних упругих сил начинает восстанавливать свою форму при этом его внутренняя потенциальная энергия переходит в кинетическую энергию движения частиц шара. Однако полностью механическая энергия шара при этом не восстанавливается, так как часть ее уходит на сообщение шару остаточных деформаций и его нагревание. Поэтому скорость шара и в конце удара будет меньше скорости V.

В рассмотренном случае скорость шара до удара была направлена по нормали к плите, такой удар называется прямым. Величина k, равная при прямом ударе тела о неподвижную преграду отношению модуля скорости тела в конце удара к модулю скорости в начале удара, называется коэффициентом восстановления при ударе:

. (5)

Значение коэффициента восстановления для разных тел определяется опытным путем. По данным опыта, при изменении скорости V не в очень больших пределах величина k зависит только от материала соударяющихся тел. Так как u V , то для реальных тел k  1.

В качестве предельного рассматривают случай абсолютно упругого удара (k = 1), при котором механическая энергия тела после удара полностью восстанавливается, и случай абсолютно неупругого удара (k = 0), когда удар заканчивается в первой стадии и вся механическая энергия тела расходуется на его деформацию и нагревание.

Экспериментальное определение коэффициента восстановления

Величина k определяется экспериментально. Рассмотрим, например, шар, свободно падающий на плиту с предварительно измеренной высоты Н. Определим высоту его подъема h после удара.

Тогда по формуле Галилея , а и, следовательно, .

Для некоторых материалов значения коэффициента восстановления (при скоростях соударения порядка 3 м/сек) составляют: дерево о дерево – 0,5, сталь о сталь – 0,56, слоновая кость о слоновую кость – 0,89, стекло о стекло – 0,94.

Прямой центральный удар двух тел (удар шаров)

При соударении двух тел удар называется прямым и центральным, если общая нормаль к поверхностям тел в точке касания проходит через их центры масс и если скорости центров масс в начале удара направлены по этой общей нормали. Таким, в частности, будет удар двух однородных шаров, центры которых до удара движутся вдоль одной и той же прямой. В противном случае удар называется косым.

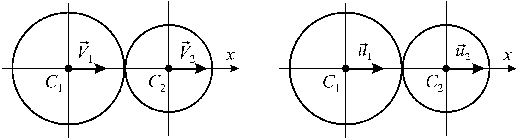
Обозначим массы соударяющихся тел т₁ и т₂, скорости их центров масс в начале удара V₁ и V₂, а в конце удара – u₁ и u₂. Проведем через центры масс C₁ и С₂ координатную ось х, направленную всегда от C₁ к С₂ . Тогда, чтобы произошел удар, должно быть выполнено условие (иначе первое тело не догонит второе). Кроме того, должно выполняться условие , так как ударившее тело не может опередить ударяемое. Легко проверить, что эти неравенства выполняются и в случаях, когда оба тела движутся влево или навстречу друг другу.

Считая m₁, т₂, и k известными, найдем . Для этого применим теорему об изменении количества движения к соударяющимся телам, рассматривая их как одну систему. Тогда ударные силы, действующие между телами, будут внутренними, и имеет место выражение .

В результате первое из уравнений (4) дает

.

Второе уравнение найдем из выражения для коэффициента восстановления. При соударении двух тел интенсивность удара (ударный импульс) зависит не от абсолютного значения скорости каждого из тел, а от того, насколько скорость ударяющегося тела больше скорости тела ударяемого, т. е. от разности (скорости сближения). Поэтому при ударе двух тел, если учесть, что всегда , а  , получим:

(6)

или

. (7)

Уравнение (7) позволяет решить поставленную задачу. Ударный импульс, действующий на соударяющиеся тела, найдем, составив уравнение для какого-нибудь одного из тел, например, для первого:

.

Последнее равенство следует из третьего закона Ньютона.

Рассмотрим два предельных случая.

Абсолютно неупругий удар (k = 0). В этом случае из уравнения (6) находим, что оба тела после удара движутся с одной и той же скоростью:

.

Действующий на тело ударный импульс при этом равен

.

Абсолютно упругий удар (k = 1). В этом случае будем иметь:

Действующий на тело ударный импульс при этом равен

.

Как видим, при абсолютно упругом ударе ударный импульс вдвое больше, чем при абсолютно неупругом. В частном случае, когда т₁ = т₂ = т, получаем

.

Таким образом, два тела одинаковой массы при абсолютно упругом ударе обмениваются скоростями.

Пример. Два шара с массами т₁ и т₂ подвешены так, как показано на рисунке. Первый шар отклоняют от вертикали на угол  и отпускают без начальной скорости. После удара второй шар отклоняется на угол . Найти коэффициент восстановления для шаров при ударе.

Решение.

По данным задачи можно определить скорость V₁ центра первого шара в начале удара и скорость V₂ центра второго шара в конце удара. По теореме об изменении кинетической энергии (на перемещении первого шара) находим:

,

где – расстояние центра шара от точки подвеса.

Отсюда

.

Аналогично находим, что

.

Вследствие того, что в нашем случае V₂ = 0, имеем:

.

Исключая из этих уравнений u_1x и замечая, что , а , получим:

.

Отсюда окончательно находим:

.